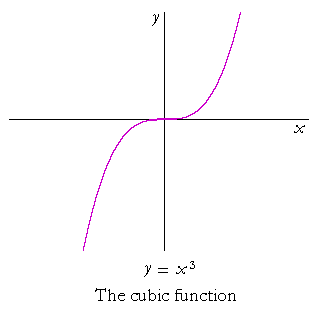These are my complete notes for Algebra II, covering such topics as Quadratic Functions, Factoring (in depth), Complex Numbers, and more.
I color-coded my notes according to their meaning - All numbered notes (which I call rules) are red, and include examples and the basis for understanding a topic. Definitions are written in green, and other important information (such as large-scale drawings that are better visualized than explained) was written in blue. All of this information is preserved on this page, with logical flow and breaks. I use ascii line drawings sparingly - If I can convey information or a graph using an image online, I will do so.
All of the knowledge present in these notes are filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Algebra II (Complete)
I. Quadratic Translation.
Fig. 1. - The Parabola:
Vertex: The furthest point to which a parabola or other function reaches within a particular restriction.
Quadratic Expression: An equation or any function expressing a parabola on a graph.
Quantity: The total in the parenthesis at all times.
Foil/Distribute: The conversion of an expression with an outer exponent ('n') into an expression repeated 'n' times, thus multiplying the expression by itself 'n' times.
Dissection of a basic quadratic equation:
┏━ Rule 1: Quantity is Horiz. & Opposite.
┏━━┻━━┓
y = -(x - 4)² + 2 <━━ Rule 1: Y-axis, normal.
┃┗━━━━━┳━━━━━┛
┃ ┃
┃ Rule 1
┃
┃
┗━━ Rule 2 for graphing, Rule 3 for Distribution.
Rule 1. Quantity, the value in the parentheses of a quadratic equation, changes the horizontal location in the opposite manner to what is expected: y = (x-4)² will translate the parabola 4 spaces to the right rather than to the left. The y-axis change comes after the parenthesis, and is done as you would expect: a -6 moves the parabola down six spaces, while +2 brings it up two. See fig. 1. for proof of these traits of the quadratic translation.
Rule 2. None of the truths of Rule 1 change when the equation becomes negative, y = -(x - 4)² + 2 is just the positive parabola upside down.
Rule 3. For -(x - 4)², the square only applies for inside the quantity, the outer negative sticks around until the end when distribution comes (opposite/reverse everything, see Rule 1).
Rule 4. The parent function (most simplified version) of all quadratic equations is f(x) = x², given the equation has an exponent no higher than 2. Transformation means to move the function along the graphical plane in some way, such as translation vertically or horizontally (as described in Rule 1).
Rule 5. The all powerful formula: g(x) = a(x - h)² + k. This formula is known as Vertex Form. 'a' is the coefficient, the number in front of x to be distributed after simplifying. 'h' is the horizontal shift (opposite, R. 1). 'k' is the vertical shift (normal, R. 1).
Axis of Symmetry: The vertical line that divides the parabola into two equal parts. h is this axis, generally.
Rule 6. In all forms, 'a' decides whether the function/parabola will be positive or negative. 'h' is the axis of symmetry and plugging in 0 for x provides the y-intercept.
Rule 7. The Standard Form equation is f(x) = ax² + bx + c. Converting to Vertex Form (Rules 5 & 6) is h = -b / 2a, and k = f(-b / 2a), plugging in h for x.
Comparison of Standard and Vertex Form:
Standard Form = f(x) = ax² + bx + c
Vertex Form = f(x) = a(x - h)² + k
Vertex a is Standard a
Vertex h is Standard (-b / 2a)
Vertex k is Standard f(plug h for x)
Rule 8. When you are dividing zero by a number, the answer will always be zero.
Rule 9. For Axis of Symmetry, always state if as x = #, not just what the # is. Remember for tests. Vertical line.
Minimum Value: The Vertex/Domain for X when the function is at its lowest point.
Maximum Value: The Vertex/Domain for X when the function is at its highest point.
Domain: The value where x exists in which X has its limits set, all real numbers within it, see above.
Range: The limits of Y, where it exists give the Min/Max value.
Rule 10. Domain is the value of x in certain imposed or natural limits, such as Max/Min values, with certain applied factors, like Decreasing or Increasing. From a vertical perspective, going up (a positive slope) is Increasing, while going down is decreasing.
Rule 11. Decreasing Domains for wave parabolas have > greater than symbols, [ 2 > x, x > -2 ]. Increasing domains use lesser than symbols, [ -3 < x, x < 4 ], Range is below. For normal y = x² parabolas, Domain = all real #s.
Rule 12. Range is the domain for Y (Domain, Range). While for parabolas X generally doesn't have a Min/Max value, Y has a Range based on the vertex. Y uses >= of <=, as it is equal and infinitely going past the Min/Max value. For a vertex of (2, -3) with a positive a, the range is y >= 3, a parabola that just stoops below and to the right of the graph for its vertex.
Rule 13. For Intercept Form f(x) = a(x - p)(x - q), converting to Vertex Form is h = (p + q) / 2, and k is plugging in h for x in f(x), just like Rule 7. See rules 5, 6 and 16.
Rule 14. Two equations use negatives, complicating matters as you have to reverse the variable based on the positive or negative nature of the # of the particular equation. For Vertex Form, reverse h from the specific equation. In Standard Form, no reversing is necessary, the equation is positive. For Intercept Form, both p and q must be reversed.
Rule 15. In equations like -x² where you have to plug in for x, the proper way to apply the number would be -(2)², applying the square first and then the negative afterwards, in the order of operations.
Rule 16. Intercept form allows you to see the x-intercepts of the equation by simply reversing p & q. This is why it is Intercept form. See Rule 13.
Rule 17. For an x-intercept of (0, 0) in Intercept form, there is a particular way to phrase it. Instead of writing g(x) = 1(x + 6)(x + 0), you cut out q from the equation (considering zero is not relevant), and place it at the front, always meaning q = 0, like so: -x(x + 6). a = -1, p = 6, q = 0. There should be no squares in the equation, see below.
Rule 18. Intercept Form is the only Parabola Form that contains no squares (rule 4). However, when there is only x-intercept, it is possible to desimplify by taking the doubled quantities of -2(x - 3)(x - 3) and squaring it to make y = -2(x - 3). This may be confused for a Vertex Form equation with a k of 0, so always half-simplify to see. You will get the same answer either way.
Pass-through Point: The point in which a particular parabola equation h is used for substitution.
Prime Factor: A trinomial or other equation that can't be factored.
Rule 19. Finding the equation of a parabola from just a point it passes through and a form-specific Indentifer is possible through substitution. Simply to get a.
a. For Vertex Form, create the equation from the known vertex to get the base equation and substitute in the known pass-through point to get a. Ex: You have the base equation of y = a(x + 5)² + 9 and the PTP is (-7, -15). You'd plug in -15 for y and -7 for x, getting the equation -15 = a(-7 + 5)² + 9. Simplify, and you'll find a = 6 and y = -6(x + 5)² + 9.
b. For Intercept Form, mostly the same thing as Vertex Form; find the base equation through the given x-intercepts and simplify using the given PTP. Ex: Base equation is y = a(x - 9)(x - 1). Plug in PTP of (0, -18), get -18 = a(0 - 9)(0 - 1). Simplifying proves a = -2.
c. Convert Standard Form to vertex and do it. Nothing special.
Rule 20. f(x) just means y, written in function form. So is g(x). They are all the same.
Rule 21. The Square root, √, is also known as a radical. √27 = Radical Twenty Seven. For the regular square root, it takes two to get out of the square using the 28|2 method, 2√7. For cube roots, it takes three to get out, turning 3√√3 for 27 into just 3. For fractions like √16 / 25, all you have to do is square root the numerator and the denominator, getting a result of 4/5. You have to apply the method to the numerator and the denominator.
II. Factoring Pt. 1.
Greatest Commmon Factor: The biggest number/factor both sides can be evenly divided by.
Rule 22. Factoring. 49x² + 42x + 9 is a Perfect Trinomial where a = √49x² and b = √9. c, 42x, is equal to 2ab, or 42x = 2(7x)(3). This is correct, so the equation can be put in (a + b)² form: (7x + 3)². Any Linear Equation in Standard Form can be solved both in Graph Form and Factor Form. For any Non-Perfect Prime Trinomial, the x-method is the way to factor any Standard Form equations: ac over b is x. Divide by the Greatest Common Factor to get the outside multiplier of the quantity when simplifying. This can be done only on one side of the equation. Factoring by grouping is fun, a(c + d) + b(c + d) = (a + b)(c + d). The internal quantity has to be the same. (a - b) and (b - a) can be made equal to eachother by making -(b - a). For four variables, this means to GCF 2 to 2, creating a grouping problem.
Rule 23. Factoring Pt. 2. For (a + b)(a - b), (a² + b²) comes out. Perfect Square Binomial, if b is a square, then you can turn x² - 25 into (x + 5)(x - 5). This ONLY works with both a and b perfect squares, don't bother otherwise. Only works with negative b. For the X method, if "= 0" is at the end, divide the Standard equation to make a = 1. Unnecessary if not. Either way, remove any fractions by multiplying everything by the denominator. ac over b is the x method:
╲ ac ╱
╲ ╱
F1╲╱F2
╱╲
╱ ╲
╱ b ╲
(F1)(F2) = ac and F1 + F2 = b.
Reciprocal: Upside down fraction, same sign.
Rule 24. Under no circumstances can there be a Radical in the denominator. Multiply both numerator and denominator by denominator to square the denominator and make it a regular integer. It would go from √49x² and b = √a / b. to √49x² and b = √ab / b.
Rule 25. Always be simplifying radicals. It is not ± √49x² and b = √28, but 28|2 → 14|2 → 7|7, ± 2√7 and b = √28. In every case.
Rule 26. Always consider leaving c on its own on one side of the equation in order to simplify a possible answer. Only if "= 0" is applied or if 100% sure that there is another method already codified can you bypass this fundamental simplification law.
Rule 27. i. i = √-1 In its most definitional sense, i is the square root of -1, an imaginary number. Complex Numbers are any equation with i, such as 2i. a + bi is the standard Form in which the solutions of the complex equations tend to take, a and b both being real numbers. Always be keepin' in mind that i maintains distinct properties than the regular algebraic variables like x and y. i may act as a normal variable at times, but when i gets multiplied by itself or by another exponent, its true self is revealed. As √-1, when squared, i becomes just -1. When cubed, i becomes -i. And when i is to the power of 4, it goes all the way to 1. This pattern repeats; to find where in the pattern any exponent lies (like i⁵⁰), divide the exponent number by 4, and take the remainder, in this case 2, and see in the patterns its equivalent. The equations are (a + bi) + (c + di) = (a + c) + i(b + d) and the negative form of (a + bi) - (c + di) = (a - c) + i(b - d). Simplify to get Standard Form. ONLY use formula if question is already in format or if can be grouped into it with factoring.
Pattern of i:
i = √-1 i⁵ = √-1
i² = -1 i⁶ = -1
i³ = -i i⁷ = -i
i⁴ = 1 i⁸ = 1
Squares to 16:
1² = 1 5² = 25 9² = 81 13² = 169
2² = 4 6² = 36 10² = 100 14² = 196
3² = 9 7² = 49 11² = 121 15² = 225
4² = 16 8² = 64 12² = 144 16² = 256
Rule 28. Quantities exist for reasons, never ignore them. If there is a negative in front of it, it will be flipped with the negative reversing everything with the Distributive Property.
Rule 29. Factoring Pt. 3. If the equation is in the correct form for X method but a != 1 and b & c aren't divisible by a, making you unable to pacify a, it is still possible factor. Go through with the process and find the quantities, say, (3x - 1)(3x - 6), the second quantity can be simplified to (x - 2), making the quantity true.
Rule 30. Factoring will not work in every case ("prime" factors), but one can still force a solution through completing the square. For an equation like x² + 16x + 17 = 0, the first move would be simply preparing the problem for applying the method: If there is C on the same side as the others and factoring has been ruled out, move C to the other side with 0 or whatever is already there. If simplification is possible, do so and try to get a as low as possible. If a is negative, multiply both sides by -1 to make it normal. Now, the equation is x² + 16 = -17. The next step is to use the equation of (b / 2)², (16/2)² in this case to get a Perfect Square Trinomial. The result of the equation is added to both sides, x² + 16x + 64 = 47. The PST nature of the left side makes it equal to (x + 8)² = 47. Square it on both sides, getting x + 8 = ±√47 Simplify if you can, if the Radical is negative put an i in front, and you should get x = -8 ±√47.
Rule 31. Completing the Square can be used as an alternate method to convert Standard Form to Vertex Form. For the equation y = x² - 22x + 16, move c to the y, and then complete the square on the right side, getting the equation of y + 105 = x² - 22x + 121. Factoring the right side gives y + 105 = (x - 11)², and moving 105 gives the Vertex Form of y = (x - 11)² = 105. (11, -105) are the coordinates. Keep C in the Y side while using the 'complete the square' method of factoring, (b/2)² to find C.
Rule 32. The Quadratic Formula works in place of factoring, completing the square, anything with regards to Standard Form, The Formula is x = (-b ±√b² - 4ac) / 2a. Example problem: 2x² + 4x - 30. 1. Always have it equal zero. 2. Simplify the base equation if you can. 3. Always have a positive a. 2 applied is x² + 2x - 15 = 0. Find a, b, and c, and plug them in to the formula. Remember PEMDAS. If √0, there's only one solution (Rule 33): try to simplify if there's a fraction.
Quadratic: Highest Exponent is Two.
Rule 33. If a Quadratic Equation EVER has an answer
D < 0: a) that includes i, the equations has no x-intercepts. This means there are No real solutions. However, this also means there will be Two imaginary solutions. This is the D < 0 property of the Discriminant, the part of the Quadratic Formula completely within a Radical: b² - 4ac. Plug in the Standard Form variables and get a solution, the Solution being D.
D = 0: b) For a Discriminant that ends up having a solution of √0, D = 0 and there would therefore be One real solution to the problem. Only when the equation is already in a completed square form ((b / 2)² appears to have already been preformed) and a = 1 can this occur, where it is very obvious. PST will always have only one solution.
D > 0: c) For a Disriminant thats ends up having two real solutions (due to the ± in the quadratic formula), D > 0 and there are two x-intercepts. Most importantly, the "number of real-imagined solutions" is for the ENTIRE quadratic equations, the discriminant only tells how many answers there will be, not what they are. "Solution" is just another word for the number of x-intercepts.
RULE 34.
COMPARISON/PROPERTIES OF ALL FORMULAS & METHODS.
Elimination, System of Equations, and Substitution are System of Equation-type methods. TRY WHICHEVER LOOKS BEST, NO ORDER.PST is a largely X-Isolation based Method. RULE 26!!!
IF NOT GCP/GROUPING, THEN COMPLETE THE SQUARE. USE QUADRATIC FORMULA AT ANY TIME.
ELIMINATION.
Formula + Description: Stack both equations like long addition and find the sum. Like System of Equations, but skipping a step. Keep two sides for factoring.Unique Trait: The goal is generally to kill off 'y' ASAP, minusing the 2nd equation (if needs be) by reversing the entire second equation. Anything to kill y.
Applicable When: ONLY to be used when both equations have roughly the same variables. Equations should generally have a y.
Limitations: Cannot be used where there is a y that is not easily solved nor where y is already known (y = 10), where substitution would be preferable.
SYSTEM OF EQUATIONS.
Formula + Description: Format the equations to both be equal to the same variable (y) and the individual non-y side equal to eachother, simplifying.Unique Trait: Only semi-self-contained method, with Elimination and Substitution both always leading to the big three. If an x² exists however, some x-isolation is needed.
Applicable When: When there is no x² or if there is only one x variable in some way. See if there can be a way to remove an entire x² or x consideration.
Limitations: If a and b both exist at the same time, then it might be easier to try Substitution or Elimination.
SUBSTITUTION.
Formula + Description: If an internal (to the left) variable has an equivalent made apparant in the second equation, plug in that equation inside the first equation. Simplify.Unique Trait: Differs from System of Equations in how one equation is replacing a variable in another, while system makes both equations equal to eachother.
Applicable When: When it is seen that substitution is viable and that it will make a difference. A definite sign of a problem requiring substitution is when more than one variable is ^2.
Limitations: Sometimes, there are no inner Equations that have a variable given an equation in the second. In these situations, use System of equations or Elimination.
PERFECT SQUARE TRINOMIAL.
Formula + Description: A Perfect Square Trinomial. (a + b)(a + b) = a² + 2ab + b² = (a + b)². (a - b)(a - b) = a² - 2ab + b² = (a - b)². Things like √x² + 6x + √9. Not ax² + bx + c, but a² + 2ab + b². Difference of Squares = (a + b)(a - b) = (a² - b²), If b and a are perfect squares.Unique Trait: PST cannot be chosen as a Method. It is a form that has its own rules. You have no control.
Applicable When: When a and b are both dearly squared. Can be forced only in particular circumstances, like if x² + 6x = -10. When a discriminant of D = 0 is found in a Quadratic Equation, the equation is PST. There will be only one solution/x-intercept.
Limitations: a² + 2ab + c² is more or less ax² + bx + c in a special format. The difference of squares won't work if even one variable isn't a perfect square (x² is a perfect square).
GCF/GROUPING → X-METHOD FACTORING.
Formula + Description: In a multi-variable equation, you can use the GCF (Max number dividable by all) to simplify. Grouping is where a GCF-ized equations gets a(c + d) + b(c + d) = (a + b)(c + d). X Method, as shown in Rule 23, is usable if the equation is equal to 0.Unique Trait: Most direct, method finds factors that multiply to ac and sum to b. Can be used for both b = 0 and a = c, b being X-isolater and c being X.
Applicable When: X method is most preferable where all fractions are gone & a = 1. However, if a != 1, it still can be done, simplifying the equation if possible at the end. Can also be done when b = 0 (in some cases).
Limitations: For X method it sometimes just won't work, such as in i in ANS is a prime. b = 0 and others work if ac is a negative perfect square. ONLY IF = 0 can be done. Group only if both GCF's have the same (c + d).
COMPLETING THE SQUARE.
Formula + Description: Force a solution by making a PST. Simplify, move C to the right: x² + 16x = -17. Use (b / 2)² for left side and add to both: x² + 16x + 64 = 47. Left is PST, (x + 8)². Sqrt both sides, x + 8 = √47.Unique Trait: A sort of hodgepodge of other methods and rules: PST, then X Method (a ± b)², the x-isolater (sqrt), & i if needs be.
Applicable When: If ANS has an i, can be used. Can be used as an alternate method for converting Standard Form → Vertex Form: Move c to y and make PST: y + 105 = x² - 22x + 121. Factor Right and move back c: y = (x - 11)² - 105.
Limitations: Will not function on if b = 0, makes the equation not work. Having an odd b also complicates matters as you have to work with fractions the entire equation.
QUADRATIC EQUATIONS.
Formula + Description: You already know what it is. Plug in a, b, x = x = (-b ±√b² - 4ac) / 2a and c from a quadratic standard form. Have a positve and simplify beforehand, when doing an equation remember PEMDAS and fractions.Unique Trait: Reversed: Solution can be returned to a quadratic equation yeezily. Get b from top left and a from the bottom. Simplify the top using x-isolator to get c. Discriminant: Inside of sqrt tells how many answers/x-intercepts there are: D < 0 is 0, D = 0 is 1, D > 0 is 2.
Applicable When: The Universal Method: Works in every case (X-mmethod not work if ANS has i and Completing the Square won't work if b = 0). Will ALWAYS give correct ANS if done correctly.
Limitations: None. If an ANS (real) is found for x with a sqrt., convert to decimal to get exact. If calculator is unavailable, simply plug in the square root for x to get an unsimplified answer.
Rule 35. When a questions asks you to "sketch the f(x)," that just means to draw a graph for the previously stated f(x).
Basic Terms of Exponents:
┏━━The exponent, a 'power' (to the power of)
5x²
┃┗━━━The base.
┗━━━━The coefficient.
Complex Number: i + real number. 2i, for example.
Rule 36. The general rule of x-isolator (described in Rule 26) is to put the individual x on one side, the c number on the other, and simplify. If there is a trinomial with both a & b, then this cannot be done. If = 0 is applied, the the "big three" of the bottom of Rule 34 are to be used more effectively. There are several rules for what is to be done if c is available and either a or b are missing.
a) If the equation uses the variables a & c in the ax² + c format, try to divide by a to get a as low as possible. Always have a positive, hopefully just x². Once that has been achieved, all that needs to be done is isolate x and sqrt both sides, getting a ± for c. This is used in an altered way by PST.
b) If the equations uses the variables b & c in the bx + c format, no prior simplification is needed. Simply isolate b and divide both sides by b. There is no sorting needed, removing the possibility of i or a number leading to two answers as seen in ax² + c format. There will always be only one solution.
III. Polynomial Functions.
Intro to Polynomials:
An expression consisting of variables and coefficients that involves only addition, subtraction and multiplication, with non-negative integer exponents. x² - 2zx + 3y, x² + 3, and 1.33ˣ + 5x are all polynomials.
Some of the lower numbered Polynomial functions have names reflecting their highest degree, as shown in the section titled "Types of Polynomial Functions" (ctrl-f).
Anything involving a radical (any kind of root, square or otherwise) or negative exponent is inherently not a polynomial by not being either a non-negative number or a integer.
x⁶ - 2√x + 3x² - 5 is NOT a polynomial. There is a non-integer exponent.
x⁶ - √2x + 3x² - 5 IS a polynomial. Everything is correct.
Types of Polynomial Functions:
Constant = f(x) = a₀ = f(x) = -14
Linear = f(x) = a₁x + a₀ = f(x) = 5x - 7
Quadratic = a₂x² + a₁x + a₀ = f(x) = 2x² + x - 9
Cubic = f(x) = a₃x³ + a₂x² + a₁x + a₀ = f(x) = x³ - x² + 3x
Quartic = f(x) = a₄x⁴ + a₃x³ + a₂x² + a₁x + a₀ = f(x) = x⁴ + 2x - 1
Standard Form: Exponents are in descending order.
Rule 37. Inequalities are Quadratic Equations that are not equal to 0 or y, but rather are >, <, ≥, ≤ to them. For the inequalities in terms of 0, an answer can be determined without the use of a graph, although the answer represents where the equation is true on the graph. The first thing to be done in an inequality-in-regard-to-zero type equation is to pretend that the equation is, in fact, equal to zero.
x² - 3x - 4 < x² - 3x - 4 = 0
Therefore, the Factoring X-Method can be done (see rule 23). Create the double groupings, very important. (x - 4)(x + 1) < 0. x = 4, x = -1. Then to fully visualize the value of x (> 0 or < 0)
in relation to the X-intercepts found, make a number line with them:
<━━━━╋━━━━━━╋━━━>
-1 4
Then, plug in 0 for x in the double groupings you already created - (0 - 4)(0 + 1) < 0. See if the answer would be negative or not. plug in the sign of the answer to the part of the line where the number was plugged in, is:
+ - +
<━━━━╋━━━━━━╋━━━>
-1 4
There is a constant pattern of negative-positive-negative-positive, so every other section of the number line can be plugged in just from one known sign. Then, you must finally acknowledge whether the original question is less or greater to zero - this gives the answer. Based on the relationhship between the number line positive-negative pattern and the greater or lesser than nature of zero. If > 0, then you are looking for parts of the number line where it is positive and vice versa for < 0. This is the case even if there are ≥ 0 and ≤ 0 in play, just replicate that sign in the answer. If the space on the line graph where the 0 attribute (whether negative or positive) is contiguous and contained within one section, so can the answer: -1 < x < 4. The answer means to set the limits for the space in which x is true according to the equation. If the equation was ≤ 0, then the answer would be -1 ≤ x ≤ 4, little difference. If the space for where x is true is noncontiguous however, such as
+ - +
<━━━━╋━━━━━━╋━━━>
where x > 0, there is a special answer template. For the example if > , the answer would x < -1 OR x > 4. These are two separate equations unified as one answer. The x < _ or x > _ is the base template. X will always come first in the equation.
Rule 38. when a questions uses the > 0 format on a number other than 0, such as 3x² - 13x + 10 > 0. Applicable anywhere. All the base algebraic properties, such as flipping the signs, still apply.
Rule 39. For Quadratic Inequalities in which the equation is unequal to y or f(x), there are special answers regarding graphing. The methodry for finding the x-intercepts is the same as for 0-type inequalities in Rule 37, but the way the graph is shown is the real way to convey what answers are true. The functions are summed up in the chart below (ALSO FIND Y-INTERCEPTS!):
If the line is linear, the same rules apply. y > means the area above the dotten line is true, while y < means the area below the line is true.
Rule 40. If there are multiple equations for y inequalities on the graph at the same time, such as y < -x² + 2x -3, then the space in which they overlap is the only true part of the graph:
This is true even if a non-equal to equation (dotted line) is used.
Rule 41. Any inequality for y or zero can be reversed in format by placing the variable at the front or the end. E.g., y > x² + 3 = x² + 3 < y. Reversing the 'than' sign is all that is needed.
Degree: Highest exponent in an equation.
Leading Coefficient: The coefficient with the highest degree attached.
Rule 42. For equations involving xⁿ exponents, for Quadratic equations and those above with exponents higher than 2, there are two very important pieces of vocabulary: Degree and leading coefficient. To find these, first sort your Polynomial equation in a descending format, with the highest exponent coming first and so forth. This should be done in any circumstance. The degree is the highest exponent in the equation, the one that comes first. in x³ - x² + 3x, the degree is three. Secondly, the Leading Coefficient is the coefficient attached to the variable with the highest degree, at the very front of the equation. There are various names for equations with different highest degrees, to the third being Cubic,, to the fourth being Quartic, etc. A detailed template of the different types of equations can be seen in the Other Important information section "Types of Polynomial Functions" (ctrl-f). For these equations to be functions, the Base needs to be x-variable, with exponent n (> 0).
Rule 43. There are several rules for Polynomial functions. For one, exponents cannot be negative - they can only be positive integers. 3ˣ, therefore, cannot be considered a polynomial. The base must be x for an exponent to be attached. To be a polynomial, the exponent has to be ≥ 0 integers. There are no rules for what the coefficients can be, only exponents and bases can have issues.
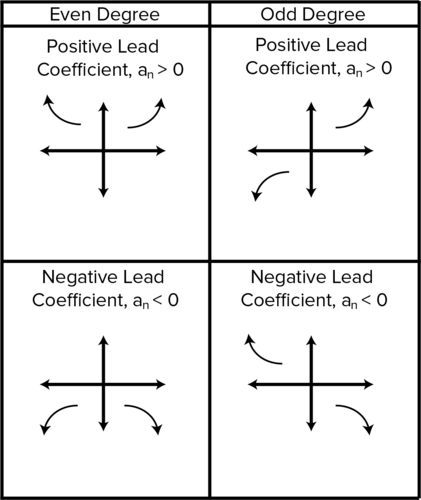
Rule 44. For all polynomial functions, the end behaviors (where x and y stretch out to infinity) can be quickly known from the knowledge of two factors: the degree and Leading Coefficient. Consult Rule 42 as to whether the Degree is even or odd and whether the leading coefficient is negative or positive. An even coefficient creates a Parabola-Shaped graph and odd one creates a graph that increases concave-down to the origin, and the concave up increases to infinity. Negative and positive Leading Coefficients invert the graphs, turning the parabolar even graph upside down and the odd graph vice versa. For a more detailed chart, see the infographic titled "End Behavior of Polynomial Functions".
What is in the middle of the graph can only be determined by either
#1. the Decreasing/Increasing characteristics for y and x, or
#2. Plugging in numbers for x to find various coordinates. For #1, see Rule 45. For #2, see Rule 46. The end behavior of a Polynomial Function is representative of where x and y will progresss going into their respective infinities:
-, + ┃ +, +
━━━━━━╋━━━━━━
-, - ┃ +, -
End Behavior of Polynomial Functions:
Rule 45. When you get several lines of information stating where f(x) is increasing, decreasing, >0, and <0, you must convert this info into line chart form before it can be in Graph form. Example: f(x) is increasing when x < 0 and x > 4. This refers to continuity templates as described in Rule 37. The line chart in this case would be:
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
For above/below zero: f(x) > 0 when -2 < x < 3 and x > 5. f(x) < 0 when x < -2 and 3 < x < 5. THe line chart in this case would be:
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
The next step would be to place the lines on top of eachother accordingly:
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
If there are five sections of the line for above and below zero, the degree is definitely even. Next, simply transcribe each segment of the graph as shown on the line:
Rule 46. This method for finding the middle section is relatively simple: just plug in various numbers for x in the equation to get coordinates. It is recommended to use all numbers -2 to 2, as that should be enough to create an accurate graph. More # can be used if necessary. Once the coordinates have been gotten, find the end behavior from the equation to make sure the coordinates are connected correctly. Plug in the coordinates to the graph and connect them correctly.
Rule 47. When a question is asking to divide a from b, the question is asking for b ÷ a. This is the case for questions of the type in both subtraction and division. For Long Division, b goes outside the box whilst a goes inside: a b .
Rule 48. For equations with three groups, such as (x + 2)(x - 1)(x - 3), multiply the first two equations first, and then multiply the result by the third group. Ex: (x² + x - 2)(x - 3). Further multiplied is x³ - 2x² - 5x + 6.
IV. Long Division.
Dividend: What is being divided from, goes inside. See Rule 49.
Divisor: What is the factor finder, goes outside. See Rule 49.
Synthetic Division: A shortcut in Long division. See Rule 50.
Subtract: Adding the opposite.
Rule 49. Long Division is mainly a continous pattern involving Elimination that goes on until it cannot. Firstly, in terms of equations such as 251 ÷ 12, 12 is the Divisor (what is divided in terms of, the factor finder) and 251 is the dividend (what is being divided from). The values are to be placed in a manner showing divisor dividend , with a space available on top for the answer. In a Polynomial Long Divison problem such as x² - 3x - 2 4x⁴ + 0x³ + 0x² + 5x - 4 , the following will be done: If the Dividend does not perfectly descend in degrees, add zeroes for those missing in the box.
The first actual step is to compare first terms: how many times does the first term of the divisor go into the first term of the dividend, or x² going into 4x⁴. x² goes in 4x² times, and therefore that variable goes atop the ^2 degree in the answer section above the box. 4x² is then distributed to every term in the divisor, the result going under the divisor. 4x⁴ - 12x³ - 8x². Then, to apply Elimination method between this result and the Dividend, flip the sign for every variable in the result, allowing the two equations to be summed. Draw a line under the original result and put out the sum. Remember to place the terms in their respective degree sections. Then, find how many times the first term goes into the first of the bottom result, repeating the entire process and adding more variables to the answer section above the box. The process ends when the first term of the divisor can no longer fit in the first term of the result, at which point the final part of long division begins.
Take the remainder and made a division equation with the remainder being over the divisor. Add this to the answer that has become above the box, and that's the answer. There is another type of Long Division that is much shorts, see in rule 50.
Rule 50. A shortcut can be used in Long Division when the divisor has an exponent of one - This is known as synthetic division. For example, take the equation (-x³ + 3x² + x) ÷ (x - 2). The degree of the divisor (x - 2) is 1. Take the base equation of the divisor and apply a simple x-isolation: x - 2 = 0, x = 2. This number will serve as Continuous Coefficient. Create a graph that looks like this: ┗━━━. Make sure there is space on the bottom. Place the Continuous Coefficient at the top left of the shape: ²┗━━━. Then, in descending order, plug in the coefficients of each variable of the dividend to the top of the shape:
2┃-1 3 1 0
┃
┗━━━━━━━━━
This is every degree down to the single, so if any variable exponent below the degree is missing, plug in zero for its place in the shape. Keep all negatives. The main method is to apply a long division-esque repeating pattern, deriving from each previous rendition. First, bring the first coefficient down below the shape:
2┃-1 3 1 0
┃
┗━━━━━━━━━
-1
Then, multiply that lower number by the continuous coefficient, plugging that new number below the second top coefficient. Sum this new number with the second top coefficient and place the result appropriately below:
2┃-1 3 1 0
┃ -2
┗━━━━━━━━━
-1
Then, repeat the cycle, multiplying the new result by the continuous coefficient and placing that number below the next upper coefficient, summing the result and repeat. Continue until you reach the final coefficient. When you have the final sum, put a box around it to separate the number from the others:
2┃-1 3 1 0
┃ -2 2 6
┗━━━━━━━━━
-1 1 3 6
The values on the bottom, other than the one in the box, can be applied to create an answer. Count how many non-box lower values there are (in this case 3). Minus this number by one. That is what the highest degree will be. With this knowledge, plug in the values as coefficients to x-bases of descending degrees: -x² + x + 3. The value in the box, 6, is the remainder, and will be divided by the divisor, (6 / (x-2)). Add this to the previously found series of values & you have the answer: -x² + x + 3 + (6 / (x-2)).
There are many applications of Synthetic Division outside of purely being a shortcut for long division, including factorization: take the question "Complete the factorization of P(x) = 3x³ - 4x² - 59x + 20, given that one factor is (x - 5)", for example. By stating that one factor is x - 5, it becomes clear that the only passage forward is by synthetic division, finding a resultant equation through dividing by x - 5. When you carry out the necessary synthetic division, you obtain the result of 3x² + 11x - 4. Through the power of imagination, you can slightly change this result to 3x² + 12x - x - 4 in order to obtain this simple factorization: 3x(x + 4) - 1(x + 4), which, as described Rule 22, is changeable to (3x - 1)(x + 4). Thus, the full factorization incorporating what we knew from the start would be (x - 5)(3x - 1)(x + 4).
Rule 51. In the Elimination method (as seen in Long Division) minusing the second equation is actually just adding the opposite, making the first variable negative even if others are made positive. That is "Subtraction" in Elimation.
V. Factoring Pt. 2.
Rule 52. Whilst a difference of cubes, as described in Rule 23, is definitely factorable, a sum of squares (x² + 64) is not. (x² - 25) = (x + 5)(x - 5). (x² + 25) is not factorable. However, a sum of CUBES (x³ + 64) is very factorable, as is the difference of cubes. See Rule 53 for more.
Rule 53. Another law of factorability is the Sum of Cubes, as well as the associated Difference of Cubes. There is an entirely different system of factoring Quantities of Cubes than for Square factoring: A difference of cubes has the base of a² - b² and is factored to the equation of (a + b)(a - b). A different of cubes, on the other hand, has the base of a³ - b³ (being to the third power and all) and is factored to the equation of (a - b)(a² + ab + b²). A sum of cubes has the factor equation of (a + b)(a² - ab + b²), having the base of (a³ + b³). As evident, the first parentheses has the same sign as the equation it factors, with as sum of cubes (a³ + b³) having a first parentheses of (a + b) while the difference of cubes (a³ - b³) has the first parentheses of (a - b). The second sign in the second parenthesis, that in regard to ab, is opposite of the sign in the first parenthesis, and therefore opposite of the sign in the original equation:
Sum: (a³ + b³) = (a + b)(a² - ab + b²)
Difference: (a³ - b³) = (a - b)(a² + ab + b²)
To perform this factorization to plug in a & b, the base equation must be cube rooted to both variables: With 8x³ - 125 for example, ∛ applied to both sides would result in 2x - 5. No ±. Remember to plug in the absolute value of a and b into the equation, getting a result of (2x - 5)(4x² + 10x + 25) where a = 2x and b = 5. Switch the sign in the original equation to a sum of cubes and the answer will be (2x + 5)(4x² + 10x + 25).
Rule 54. On Factoring Completely, arguably the final key in the great constant of factoring. There are various rules, but most of the previously known concepts, such as GCF, still apply, but just on a larger scale with more steps. Complete Factoring incorporates the newly discovered Sum & Difference Cubes into trinomial Cbic equations. Generally, the first step in factoring a trinomial with a degree of three or greater (if another factoring option is not already obvious) is to GCF the entire equation. For example, in the equation x³ + 10x² + 24x, the GCF that can be removed is x, making the equation x(x² + 10x + 24). Now, the inner equation can be given the X method:
╲ 24 ╱
╲ ╱
0 ╲╱ 4
╱╲
╱ ╲
╱ 10 ╲
The completely factored equation is now x(x + 6)(x + 4), nothing more can be done. If exact answers as to what x is equal to are needed, than the outer x = 0, and x = -6, x = -4.
Factoring Completely is just a multistep, a more advanced form of factoring. However, one must always be checking if more can be done. For a complete simplification after a PST has been discovered, such as 6(x² - 4x + 4) factored into 6(x - 2)(x - 2), the equation can be condensed to 6(x - 2)².
An example of a furtherly elaborate equation is -16x⁵ - 250x². GCF: -2x²(8x³ + 125). Now, the internal equation is evidently in a sum of cubes (both the degree and the coefficient of a can be cube rooted). Cube rooting gives (2x)³ + (5)³, giving a = 2x and b = 5. The correct formula for a sum of cubes factorization is (a + b)(a² - ab + b²). All that's left to do is to plug in a and b, and Remember to put the GCF in front of the equation, kept for the entire problem. The answer would be -2x²(2x + 5)(4x² - 10x + 25). Equations with four variables can be dealt with the same way they always have: GCF-ing the first two and the last two separately, grouping. The paranthesized equation for each side should be the same: x²(x - 2) - 9(x - 2). As obvious, merge the sides and create (x² - 9)(x - 2). However, as Complete Factoring entails, there is more to be done: The first equation is a difference of squares. Therefore, the completely factored y is (x - 3)(x + 3)(x - 2), or x = 3, x = -3, x = 2. The "more that can be done" is almost always a difference of squares or sum/difference of cubes. In fact, in some cases, GCF is not immediately usable and the equation can just quickly be given using difference of squares or a sum/difference of cubes. Even if the equation looks quite complicated.
ALWAYS be checking if the coefficients or bases in the equation are Perfect Squares or Cubes, as this is a shortcut to the answer. Of course, the degree of a base (the exponent of x) being a perfect square or cube just means it is divisible by 2 or 3. An example of this shortcut is 625x⁸ - 256. On the surface, there is no easily identifiable GCF. Therefore, it must ascertained that the equation is a difference of squares and can have those properties applied. First, square root both sides (25x⁴)² - (16)². Using a standard formula, this equation is now (25x⁴ + 16)(25x⁴ - 16). Hilariously, the second equation is another difference of squares, and therefore more factoring can be done. The result/final answer is (25x⁴ + 16)(5x² + 4)(5x² - 4), nothing more can be done.
Rule 55. How can it be that X-Method is still applicable to non-quadratic equations? Well, it is possible to make an educated guess as to what the factors will be considering that exponents add when multiplied. In the equation 2x¹³ + 10x⁹ + 8x⁵, for example, after GCF it is 2x⁵(x⁸ + 5x⁴ + 4). Using the power of imagination, simply perform X-method normally and divde the degree by two and get a correct answer: 2x⁵(x⁴ + 4)(x⁴ + 1). This strategy will sometimes not work so use a mental trial and error to factor. The strategy generally works when the exponent of b is half of that of a.
Rule 56. As repeatedly stated in Rule 54, Complete Factoring sometimes allows for the values of x to be found. However, this should only be done when the question is specifically asking for it or is equal to 0. "Find the zeroes" provides different final answers than "Factor the Polynomial Completely", the latter stopping short of finding the values of x. As stated before, if an X is GCF-ed to the front of the equation, then it is automatically equal to zero.
Rule 57. Similar to a previous Rule of Thumb of simplifying a to zero when possible, Factoring out a negative in Complete Factoring whenever possible is a must, for not doing so could lead to an incorrect answer. It just makes things way easier in general.
Rule 58. Specialties of finding the values of x in situations somewhat specific to Complete Factoring: When after X-method the x base is still exponential (in a manner described in Rule 55) and the question wants an exact values for x, then give a ± √ with the same root as whatever degree x is for the answer. Having the value not being perfect is a prerequisite. Think of this like an exponential form of Rule 29. Another way to represent the values of x is with curly brackets, as in x + {2, 3, 0}. Also, sometimes solutions can be repeated. Just keep one.
Solutions are zeroes are x-intercepts.
Rule 59. The existence of the ± when square rooting is only made by the answer being X, such as x² = 4. It wants to catch all positive values of x. If the statement is simply √4 however, the answer is just 2. Continued at Rule 64.
Rational Zeros Theorem:
If F(x) is a polynomial function with integral coefficients and if p/q (a rational number in lowest terms) is a zero of F(x), then p is a factor of the constant term of F(x), and q is a factor of the leading coefficient of F(x).
*we can use the Factor and Remainder Theorem in tandem with this.
Take F(x) = 9x³ - 18x² + 11x - 2, for example. The constant term at the end of the function is 2 (always make the number positive, because the list of (p / q) itself will be ±), and so the factors for p are 1 and 2. The leading coefficient of the term with the highest degree is 9, and so q is equal to its factors: 1 and 9, and 3 and 3. The Rational Zeros Theorem says that if there is going to be a rational zero for this polynomial, it must be in the list of P's over Q's:
p = ± {1, 2}
q = ± {1, 3, 9}
(p / q) = ± {1/1, 1/3, 1/9, 2/1, 2/3, 2/9}
Unironically, the best move right now is to plug in each one of the damn p/q's until you find a zero. Once you have at least one, then you can use synthetic division to find the rest:
F(1) = 0
By synthetic division, F(x) / (x - 1) = 9x² - 9x + 2.
Thus, 9x² - 6x - 3x + 2
3x(3x - 2) - 1(3x -2)
(3x - 1)(3x - 2)
Thus, (x - 1)(3x - 1)(3x - 2) are the zeroes of the function.
When you have a particularly lengthy problem in which the degree is greater than 3, such as 2x⁴ - 9x³ + 4x² - 35x - 50, applying the Rational Zeros Theorem and then Synthetic Division will still leave you with unfactorable problem: 2x³ - 11x² + 15x - 50. Thus, you simply have to do entire process again on that lower polynomial. Repeat until you reach an easily factorable bottom. If you reach the bottom and have found a non-easily factorable answer, such as, in this case, f(dx) = 2x² - x + 10, use quadratic formula, obviously. If you end up with imaginary answers, then just leave your answer as an unsimplified form using the zeroes you found before using synthetic division: (x + 1)(x - 5)(2x² - x +10).
In order to find a polynomial from the roots, you just need to multiply the roots (in their x + or - form) and see what you get. For example, given the roots x = 3, x = -4 + 3i, and x = -4 - 3i, then one can multiply them together as so: (x - 3)(x + 4 - 3i)(x + 4 + 3i). This multiplies out to x³ - 5x² - 15x - 27.
The Fundamental Theorem of Algebra:
For every polynomial function with the degree of "n", there are exactly "n" zeros, real or imaginary, rational or irration.
For example, f(x) x²³ - 15x¹⁹ - 1 has 23 zeroes, because of the degree. This can be used in conjunction with another theorem:
The Conjugate Zeros Theorem:
States that if P(x) is a polynomial with real coefficients and if (a + bi) (where a and b are real and b ≠ 0) is a zero of P, then (a - bi) is also a zero of P.
Complex roots/solutions/zeros with non-zero imaginary components ALWAYS come in pairs. (a ± bi)
You can NEVER only have one zero with an imaginary number. The Conjugate Zeros Theorem will not allow it. See the diagram below for proof (and also for help for Descartes' Rule of Signs):
Descartes' Rule of Signs:
Gives us an idea of how many real zeros there could be in a polynomial, and whether they are positive or negative.
(1) The number of positive real zeros equals the number of variations in signs of the coefficients of P(x), or is less the number of variations by a positive even integer.
(2) The number of negative real zeros equals the number of variations in signs of the coefficients of P(-x), or is less the number of variations by a positive even integer.
Take this polynomial for example: P(x) = x⁴ - 2x³ - 2x² + 3x + 1. In this polynomial there are two sign changes, seen after the first term and third term, and so there are 2 or 0 positive real zeros, given 1) of Descartes' Rule of Signs.
When you plug in -x in order to find the negative real zeros, you get P(-x) = x⁴ + 2x³ - 2x² - 3x + 1. There are also 2 sign changes here, and so there are either 2 or 0 negative real zeros.
Thus, the polynomial can have any of the following:
2 positive real zeros and 2 negative real zeros
2 positive real zeros and 2 non-real zeros
2 negative real zeros and 2 non-real zeros
4 non-real zeros
This can occasionally be useful when used in conjunction with other theorems.
VI. Rules of Exponents.
Rule 60. As with all other exponents, graphing Vertex form equations cubed has the same rules as when graphing them squared, where values inside the quantity (the parentheses) effect the x opposite to the sign (Rule 1), and values added/subtracted to the right being reflective to the y and applying as the sign states. Obviously, the shape of a cubed vertex form graph is different than that of a squared one. The basic curve of a cubed function (that is to say y = x³), is this:
Rule 61. To discover whether a function is even or odd (other than the nature of the leading coefficient) given that the function is a Polynomial, plug in -x for y and see what you get. For example, in the equation g(-x) = 3x² - 7, the x is substituted for 3x² - 7, which causes no change as the negative gets squared. As the equation is the same as before the substitution, the equation is even. A guide to determining Positivity/Negativity is below:
Opposite: Odd equation.
Result is...* Same: Even equation.
Half: Neither!
*compared to before substitution.
Don't ask what Neither means.
Generally the appearance of odd or even functions will follow the below format:
Rule 62. Cubic Functions are functions in which there are three X-method-esque values of x, such as (x - 2)(x + 3)(x + 4). The basic equation that these functions follow is f(x) = a(x - x1)(x - x2)(x - x3). In a basic equation where f(x) = (x + 4)(x - 3)(x - 6), with a being equal to 1 of course, the solutions would be x = -4, x = 3, and x = 6. The coordinates for this equation can be given as (-4 ,0), (3, 0), (6, 0), (0, 0), the final point being the y value that gets plugged in for f(x) so the solutions can be found. One group of coordinates that can be used to reverse create a cubic function is (-4, 0), (1, 0), (3, 0), (0, -6). Since the final point is a value for y, it must be plugged into the f(x) to get the value of a. Thus, the equation will become so: -6 = a(4)(-1)(-3). Plugging in the y point also plugs in zero for x. Simplifying leads to -1/2 = a, resulting in a finished product of f(x) = -1/2(x + 4)(x - 1)(x - 3)
Rule 63. Rational Exponents are essentially properties about how equations regarding exponents can be conducted. There are six main Holy Properties as it were, while the pt. 2 expansion of the properties contains another three. The first and most prevalent of the properties is the all-powerful:
1. am/n = n√aᵐ
- the universal property. When in doubt, try Holy Property #1. With this property, a sort of subproperty emerges stemming from how when m = 1, the equation just becomes n√a: Simply, a1/2 = √a. A constant rule that must be kept in mind for all of the properties is how the properties can be reversed depending on the equation and that transformation needing to be performed. For instance, √6 can just as easily be changed into 61/2 as it could be done the other way around. For an example of property #1, 644/3 = (∛64)⁴, which can be further simplified to (4)⁴, with a final answer of 256. One important thing to remember is how negative exponents just place the equation as the denominator in a fraction, for example 5-2/3 is just equal to (1 / 52/3), where nothing else can be done (Property #1 would render no further results). An example incorporating Property #1 is 16-5/4, where (1 / 165/4), = (1 / (∜16)⁵) = (1 / (2)⁵) = 1 / 32.
Rule 64. Continuation of Rule 59. While all "x = " equations with an even exponent create ± scenarios, double answers, Odd exponents only ever lead to direct answers, negative or positive depending on the original equation. For example, x³ = 64, and ∛64 only has one solution: 4. ∛-64, on the other side, also has but one answer, -4. An even exponent/index with a negative radicand, such as √-64, would lead to a complex answer, specifically 8i.
Rule 65. While for exponents on the same plane of existence that have coefficients being multiplied can simply be added (for example, exponents that are fractions must have their common denominators found to be added, 131/3 × 131/6 = 132/6 × 131/6 = 131/2), exponents on the outside of a parenthesis, such as (3⁵)⁶, have their exponents multiplied: 3³⁰. There are multiple planes of existence in which exponents or whatnot can appear: the first plane is within the parenthesis, the second is just outside, and the third is outside the brackets that enclose the previous two planes. For example, [(3⁵)⁶]³ is equivalent to (3³⁰)³, or 3⁹⁰.
Rule 66. The second rule of the holy properties is:
2. (ab)ᵐ = aᵐbᵐ
The more advanced brother of property #2 is property #3:
3. (aˣbʸ)ᵐ = aˣᵐbʸᵐ
An example of this is (51/5 × 81/3)⁵, which is equal to (51/5)⁵ × (81/3)⁵, where nothing else can be done. A good reversal of Property #2 can be seen in how 3² × 2² is equal to (6)². With x, Property #3 can still be conducted: (3x²)³ = 3³x⁶ = 27x⁶.
Rule 67. The Reason for why the exponent of 0 is equal to 1 in all circumstances is because of base-2: All descending powers of 2 are dividing by 2, ex. 2³ = 8, 2² = 4, and 2¹ = 2. Therefore, it would only make sense if it kept dividing by 2 after that, so 2⁰ = 1, 2⁻¹ = 1/2, 2⁻² = 1/4, and so on. For aesthetics.
Rule 68. Property #4:
4. (aᵐ) / (aⁿ) = aᵐ⁻ⁿ
This property is the only other completely unique property (in that it is not derived from any of the others) after Property #1, and I consider it the second most important property in terms of usage and all-encompassing nature. While Property #1 covers exponents that are fractions, Property #4 covers exponents within fractions. Of course, the scope of Property #4 is somewhat limmited due to the coefficients in both the numerator and denominators, a, need to be the same. The most simple example of the rule in action would be (4² / 4⁷) = 4⁻⁵, but a better, more intricate example incorporating Property #5:
5. (aᵐ / bᵐ) = (a / b)ᵐ
(which, upon first glance, may appear to be a spin on Property #4, but is really just another one of the Equivalence Properties) would be (561/4 / 81/4)³. Since the coefficients are different but the exponents are the same, Property #5 is used to create a multi-layered triple-plane equation: [(56/8)1/4]³. The internal fraction is easily divisible, removing a plane: (71/4)³. With simple multiplication the final answer of 73/4 is reached. Another equation specifically for Property #5 is (3x/2)⁴, which requires a reversal from the property. Applying the exponent to a, 3x, means to apply it to both the coefficient and the x: 3⁴x⁴, or 81x⁴. 2⁴ is 16, so the answer is 81x⁴ / 16.
Rule 69. Finally, Property #6:
6. n√a × n√b = n√ab
This property opens the rabbit hole into how square roots can be multiplied and divided, which has many subrules to remember. A simple example for the property is ∛4 × ∛128. Since too much mental power is require to ∛4 × 128, you can just factor 128 without multiplying:
128┃4
32┃4
8┃2
4┃2
2┃2
Thus, ∛4 × 4 × 4 × 2 × 2 × 2, including the unmultiplied 4, has two sets of triplets that can escape the cube root, 2 and 4, which multiply on the outside to make 8. Now, a fundamental rule that governs all the properties except perhaps for #1 and #4, is that exponents can be swapped out for roots and the property will still function. For example in Property #5, replacing m with n√ creates a child property to be remembered, (n√a) / (n√b) = n√(a / b). A good example of this is (5√192) / (5√6), which is turned to simply 5√192 / 6. Performing the internal division results in just 5√32, which is 2.
When there is a negative on the outside of the parentheses, swap the internal nominator and denominator and make the outer exponent positive. This may only be done when there is an outer left negative and where there is an outer right exponent that is negative as well.There is a reocurring role in fractions that there must never be a radical on the bottom and that if there ever is, it must be removed. This is done through mulitplication, like so:
2 × √3 2√3
━━ = ━━━
√3 × √3 3
Keep in mind that different radicals lead to different simplifications; take (∜19 / ∜4), for example. The first step is to multiply top and bottom by ∜4, in the same manner as shown above. However, in this case multiplying out the bottom will not make the denominator 4, as would be the case if it were a square root. Instead, as evident if actually multiplied out to ∜16, the result is 2 due to the heightened index/root, for a full answer of (∜76 / 2).
For odd indexes/roots, such as cubed roots, the complexity increases as the denominator can no longer be used to multiply out the bottom radical, it will have no effect. Therefore, another number must be found that will create a perfect cube in the denominator when multiplied. For example, (2 / ∛3) must be multiplied by a number that will turn the radical 3 into 27, the closest perfect cube that has a factor of 3. Therefore,
2 × ∛9 2∛9
━━━ = ━━━
∛3 × ∛9 3
The simple way for knowing how to multiply radicals and their coefficients as long as they have the same index/roots is through this example: (3√2)(5√3) = 15√6. As you can see, coefficients and radicals multiply separately.
Rule 70. The conjugate is a very useful tool for equations with a radical denominator with multiple unsimplifiable variables. The conjugate is, simply, the denominator with everything the same except for the sign in the middle. For example, the conjugate of √7 - 2 is √7 + 2. The conjugate of -3 - 2√5 is -3 + 2√5. Quite simply, the purpose of the conjugate is to multiply the nominator and denominator of one of these strange equations in order to remove the radical, the conjugate being just a special means to achieve that goal. For example, an actual equation in which the conjugate would be used is 1 / (√7 - 2), simple enough. Multiplying the conjugate is step one:
1 × (√7 + 2)
━━━━━━━━━
(√7 - 2) × (√7 + 2)
The bottom, after simplifying and cancellations, is equal to 3. The top, having been one, makes the answer simple: (√7 + 2) / 3.
Rule 71. When conducting an addition or subtraction equation between two radicals and their coefficients, try to simplify to make the radicals the same. In 5√12 - 19√3, simplifying √12 makes the first variable 10√3, which can be used in the equation to create -9√3. Simply put, not having the same radicand initially doesn't mean permanently.
Rule 72. The second part of the properties of radical equations is mainly just a summary of all the unusual side-effects of the properties from the first part. For example, the first side-effect is that for radicals where n√xⁿ, there are different possibilities for what x is equal to depending on whether n is odd or ever. This is due to negative numbers in even roots being taboo. If n is odd, then n√xⁿ = x, completely free no matter if x is negative or whatnot. ∛5³ = 5 and ∛(-5)³ = -5. Free country.
If n is even, however, then n√xⁿ = |x|, the absolute value of x, making it possible every time. ∜2⁴ = 2 and ∜(-2)⁴ = 2. 1984.
Keep in mind that when a letter variable like x is an even n equation, the absolute value symbols must remain with it in the answer: ∜x⁴ = |x|. Same internal exponent + same index = cancels out. When trying to create a n√xⁿ equation when the second n is greater, GCF the radicand to find something that will be able to be on the outside. Remember that when a variable that still has an exponent attached is spit out of an even n equation with an absolute value around it, such as |y⁴|, if the exponent is even, then the absolute value is to be removed as the exponent will cause it to be even either way. "Assume all variables are positive" relieves you of having to put abslute value. For the exponents of variables in the radicand, simplifying to see what you can't take out is as simple as dividing the exponent by the root, applying the result as the exponent of the variable on the outside, and using the remainder as the exponent of the variable on the inside.
Rule 73. This is just another means of simplification you've pretty much solved the equation: If a perfect square/whatnot must be left in its radical (∜4), you can square or whatever root it internally: ∜2². Optional.
Rule 74.
Not to be disclosed under ANY CIRCUMSTANCES!
If an internal Radicand is a perfect square and the index/root is even (∜1296), square root the radicand and divide the index by 2: √36. A Completely Legal move.
Rule 75. The second side-effect is another relating to fractions, but this is a bit of a tool to help you in solving variable and exponent packed equations. As you know, z⁻² = (1 / z²). As this logic would follow, (1 / z⁻²) = z². For example: (16xy1/3 / 8xz⁻⁴), the z can be moved to the top because it has a negative exponent in the denominator: (16xy1/3z⁴ / 8x).
Rule 76. (x² / x¹⁰) = (1 / x⁸). This is way faster than actually minusing 10 from 2 and going x⁻⁸ = (1 / x⁸). Just denominator exponent - nominator exponent.
One-to-one function: Any function that passes both the vertical and horizontal line test, e.g. it can have an inverse function.
Inverse Functions:
In an abstract sense, while a function is a relation between an input and an output such that there is only one output, the inverse function is taking the original and performing it in reverse order with the opposite operations. For example, if you have the function f(x) = 3x + 2, you are first multiplying by three and then adding by two. The inverse function would subtract by two and then divide by 3.
In a more practical sense, the inverse of the function is that in which the x and f(x) are reversed. For example, if you were to take this to be the output of the original function:
x ┃ y
━━╋━━
-2┃-4
-1┃-1
0┃2
1┃5
2┃8
Then this would be that of the inverse function:
x ┃ y⁻¹
━━╋━━
-4┃-2
-1┃-1
2┃0
5┃1
8┃2
How do you get the inverse function? Easily. ALl you have to do is take the original function, say y = (x / (x + 2)) and switch around y and x:
x = (y / (y + 2)). Then, all you have to do isolate y to find to find the inverse equation:
(y + 2) × (y / (y + 2)) = (y + 2) × (x)
y = xy + 2x
y - xy = 2x
y(1 - x) = 2x
y = 2x / (1 - x)
As we all know, a graph must pass the vertical line test in order to be considered a function. However, there is an additional horizontal line test that must be used to determine whether a function has an inverse. Take y = x², for example. This parabola clearly does not pass the horizontal line test, and so does not have an inverse in any official sense. However, if you were to switch around y and x and isolate y as you would for a regular inverse, you would find that the "inverse" is y = ±√x. However, as we know, this is not a 'real' inverse.
If there are five sections of the line for above and below zero, the degree is definitely even. Next, simply transcribe each segment of the graph as shown on the line:
As you can see, y = x² does not pass the horizontal line test while the combined graph of ±√x does not pass the vertical line test. You cannot have an inverse function that is not a function, so x² does not have an inverse, because it is not a one-to-one function. However, we can create a restricted inverse function by creating restrictions upon the domain of y = x² and ±√x, x² being restricted to ≥ 0 while √x is restricted to y ≥ 0. This creates one-to-one functions in both functions, making them proper inverses of one another.
Note the symmetry of the restricted graph - inverse functions always mirror eachother along y = x.
In order to test whether two functions are inverses of one another, plug in and test these formulas to make sure they are true:
f(f⁻¹(x)) = x
f⁻¹(f(x)) = x
This is given any x value. Considering how the y values of f(x) are the x values of f⁻¹(x) and vice versa, this approach makes perfect sense.
Summary of Inverses:
-The domain of a function is the range of its inverse.
-The range of a function is the domain of its inverse.
-The inverse of a function is its reflection across the line y = x.
-Domain restrictions must be stated for inverse functions, because only one-to-one functions have inverses without domain restrictions!
NOTE: The inverse is not always the negative reciprocal. Negative Reciprocals are mainly used to find the slope of a line perpendicular to another, as described in rule [[[[[[[[[[[.
