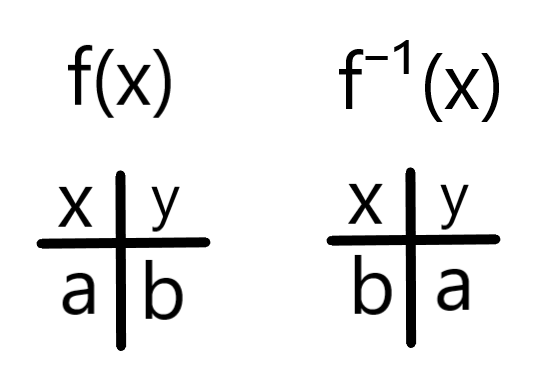These are my complete notes for Precalculus, covering such topics as Piecewise Functions, Composite Functions, Complex Fractions, Inverse & Parent Functions (in greater detail), Logarithms, Degrees and Radians, Trigonometry, Sinusoidal Waves, and more.
I color-coded my notes according to their meaning - All numbered notes (which I call rules) are red, and include examples and the basis for understanding a topic. Definitions are written in green, and other important information (such as large-scale drawings that are better visualized than explained) was written in blue. All of this information is preserved on this page, with logical flow and breaks. I use ascii line drawings sparingly - If I can convey information or a graph using an image online, I will do so.
All of the knowledge present in these notes are filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Precalculus (Complete)
VI. Rational Equations.
Cross Multiply: Multiplying two fractions diagonally - can be done when two fractions with variables are equivalent.
Least Common Multiple: The smallest number that two or more numbers can divide into evenly.
Rule 78. Cross Multiplying is to be done in situations where there are two (2) fractions that are equal, such as (3 / (x + 1)) = (9 / (4x + 5)). This only works when both variables are by themselves.
Rule 79. Another means of finding whether an equation was extraneous or not in the fastest possible way - a rule of thumb is that if you plug in an answer you got for x in the denominator and it does not go to zero (illegal), then it is very likely to be the answer. Only use this trick in a pinch!
Rule 80. One of the more convenient aspects of the least common multiple is that, in general, it removes the denominator due to the cancelling outs. However, the goal is always to have it so that the denominator for all variables is the same, whether that be 1 or some LCM frankenstein. Always eyball beforehand whether cancelling out will grant an opportunity where all denominators are equal. For example, in the post-LCM equation (20x / x) + (28x / 4) = (-36x / x), the option is available to simplify each equation and therefore to remove all denominators. What out! It is your decision whether to multiply the denominator or not.
Rule 81. When you have gotten all variables to agree on a denominator other than 1., remember that you must simply sum the top of its plus & minuses if you want to cancel out more. For example, in the equation (5x + 3(x + 3)(x + 4)) / (6x(x + 3)), (x + 3) cannot be canceled out because there is an addition ongoing in the numerator.
Rule 82. All inequalities in regard to x (representative of the domain), such as x ≤ 12 or -4 ≤ x < -1, can be represented through interval notation. Simply, the postion of the number in the coordinates represents where the x is located between. For example, -4 < x < 2 would be (-4, 2). If an equation contains an x that goes in one direction infinitely, such as x > 12, than the infinity is used: (12, ∞). Infinity is always done with a parenthesis, as it cannot be contained. The first variable in the coordinates is the lowest possible value that x can be, naturally, and vice versa goes for the second variable. For greater or equal to symbols in the equation, whichever side has the ≤ (first or second) has a bracket used for it instead of a parenthesis. For example, -8 < x ≤ 20 = (-8, 20]. Remember that infinity can never have brackets. on a number line, a closed circle means not equal to, while a filled one means it is. For equations using the "or", a special character is used to denote these separate possibilities and limits: ∪. The Union symbol. For example, in the equation x ≥ 9 or x < 2, the coordinates would be rendered as (-∞, -2) ∪ [9, ∞).
Rule 83. As is known, a function is that which passes the vertical line test. If a vertical line intersects more than one point on the graph, it is not a function. For example, on a number chart for coordinates, X-values cannot repeat, while y values can repeat and still be a function.
Rule 84. For equations where there is an equation to solve regarding y and x, such as y² - 2x = 5, simplify as much as you can for either one and then plug in 1 for the unsimplified side's variable, in this case x: y = ±√2x + 5 = ±√7. Because the value of y is ±, there are two different values of y for one (1) x, making the equation not a function. Simply put, a ± in the value of the y makes it not a function.
Rule 85. Believe in yourself! :3
Rule 86. There are special rules for more abstract equations regarding concepts like square roots that require advanced levels of thinking. For example, in the equation g(t) = √t - 5, you must know that t - 5 ≥ 0 because a negative has no real square root. Therefore, the Domain of this equation is all real numbers that are ≥ 5: [5, ∞). Be creative! For equations that don't involve radicals, such as 3y = 11 - 4x, it is pretty much always a safe bet that the equation is a function. Squares and other regular exponents are also pretty much fine.
Rule 87. For f(x)-type equations where you plug in things for x and whatnot, more advanced and spectacular variables can be plugged in for x, just for fun. g(5x + 4) = (5c + 4)² + 8(5c + 4) - 24. Once simplified, you will find 25c² + 80c + 24, totally meaningless.
Rule 88. Another type of equation where there are Domain specificities are those where it is a fraction with a variable involving x on the denominator, such as f(x) = (2 + x) / (x² + 7x). There is nothing really to do in this equation other than finding the values that would make the denominator equal to zero, a fun game. The first step would be to simplify the denominator as much as possible, GCF and all that: x² + 7x = x(x + 7). Off the bat, you can easily tell x can't be 0, and two seconds later that x can't be -7. Therefore, the Domain is all real numbers except for x = 0 & x = 7.
Rule 89. There is a special method for plugging in x into an equation. The best way to think about it is as a computer code conditional if statement. This is a piecewise:
| 1.6x - 41.6, if 63 < x < 66
h(x) = { 3x - 132, if 66 ≤ x ≤ 68
| 2x - 66, if x > 68
Only one equation belongs to each value of x. You just go ahead with a regular 'plug-in-for-x' type problem once you know what x is. There are no special rules, it is that simple.
VII. Domain and Symmetricality.
There can be graphs that can show disconnected lines, where functions like so:
show a puzzle to figure out what is Domain and Range, while other graphs can also use tons of dots at important points to represent whether a high/low point is included in the line. For example, in the given graph, because the highest point of the left part is an empty circle, then that point unincluded in the leftmost interval. The full interval notation would be (-8, -3) ∪ [-1, 5) ∪ (5, 8].
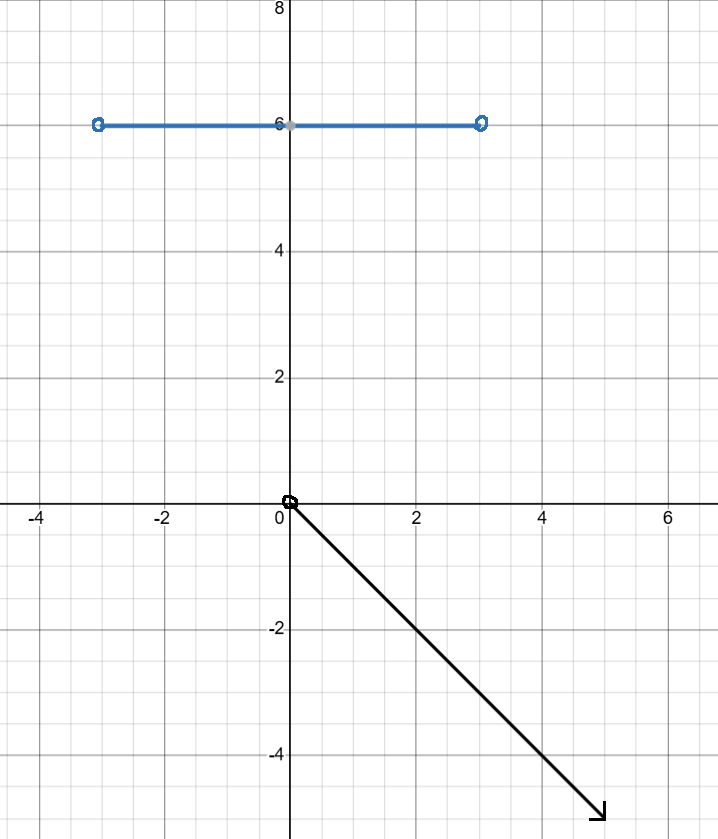
Rule 91. When you have a disconnected line graph, you may see that there is either a vertical or horizontal flat line. If the flat follows its respective register, such as a flat line following the x-axis when you're writing domain, no problem. But when you come across the same line while writing range, there is a special way of writing it: For a graph like this -
the first part of the interval notation would be (-∞, -2) ∪, with the down-to-up rule and all, but the second part would be represented as [6]. For either Domain or Range, brackets or parenthesis on a single digit means flat.
Rule 92. The y-intercept is found by plugging in 0 for x, f(0). The x-intercept is found by plugging in 0 for y, "0 = ax² + bx + c". X-intercept are also known as the "zeroes" and "roots" of the function.
Rule 93. There is symmetry test that can be conducted for every axis, x, y, and origin.
In relation to the x-axis:
In relation to the y-axis:
In relation to the origin:
For the origin, fold first on x and then on y. To discover algebraically if it is symmetrical on any axis, you must plug in a negative for whichever vairable you feel the equation may be symmetrical for:
X-Axis: (x, y) = (x, -y)
Y-Axis: (x, y) = (-x, y)
Origin: (x, y) = (-x, -y)
In general, for equations like x = y² - 3 or whatnot, the variable that has the square is immune to becoming negative because of the automatic squaring, so it is highly likely in said situations that a shortcut can be taken to find what axis the equation is symmetrical on. However, it is always safer to plug in the negative for each possibility to discern whether the less obvious possibility is symmetrical as well. Multiple tests should be performed if you are not sure, in order to make sure that your first test was not just a coincidence.
# Rule 94. There are two ways of checking whether an equation has a symmetricality in any way: Numerically and Algebraically. Numerically, you would plug in actual numbers for x and y and see what the equation would simplify to normally as a control group. For example, y = -x² + 6 is simplified to y = x² + 6. From there, plugging in (2, 2) resolves the equation to 2 = 10. This is the answer to be expected for any symmetry check to be correct - differing sides. Checking the Y-axis, for example, means plugging in (-2, 2), equal to 2 = (-2)² + 6. Simplifying this returns, once again, 2 = 10. These results mean that symmetry hath been confirmed. To check algebraically is much simplier, you need not plug in any values but the exact negativized variables from the original equation - E.g., plugging in (-x, y) for y = - (-x)² +6. Since the outer negative remains as before, symmetry has been proven both ways.
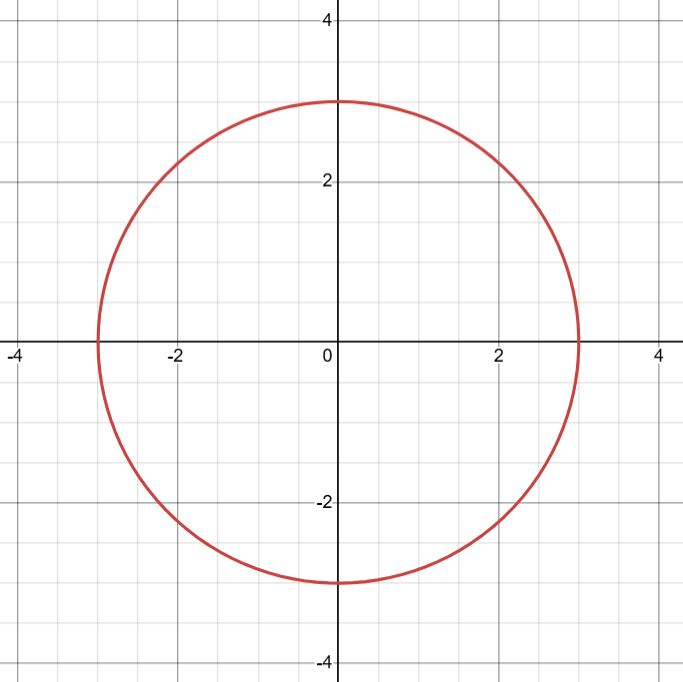
# Rule 95. A perfect circle centered around the origin, like so:
would be symmetrical by both the x, y, and origin axis. Both the x and the y would be squared in the equation: (x+h)² + (y+k)² = r².
# Rule 96. For the symmetries, there are general "odd" and "evens" that can be applied to the symmetry of an equation:
Symmetry in respect to X-Axis: Odd
Symmetry in respect to Y-Axis: Even
f(-x) = -f(x): Odd (Opposite)
f(-x) = f(x): Even (Same)
Apart from the application of the symmetries, this is a return to Alebra 2, as the x plugged in (checking the Y-axis), gives three possibilities:
Odd, if the returned f(x) is equal to the opposite of the original, Even, if the f(x) is the same, and Neither, for those in between.
VIII. Parents, Composition, and Inverse.
(f(x₂) - f(x₁)) / (x₂ - x₁)
To perform the process, you need two bits of information: The point [x₁, x₂], and the equation.
First, keep in mind that [x₁, x₂] = (x₁, f(x₁)) and (x₂, f(x₂)). Then, simply go about plugging in the points in for x of the equation. For example, with the points [-2, -1] and the equation f(x) = -x³ + 3x, -2 would produce 2 and -1 would produce -2, creating the points of (-2, 2), (-1, -2). In plugging in these numbers to the formula, make sure to keep all negatives as the negatives in the formula can be subject to change, such as when f(x₂) or x₂ are negative. For this example, (-2 -2) / (-1 + 2) = -4/1, = -4.
You don't need to worry about if the points are both x or not, you just need to find f(x₁) and f(x₂) and plug them into the equation.
# Rule 98. Families of functions are groups of functions with graphs that display similar characteristics. The parent function is the skeleton key function, the simplest of functions in a family. It is the function that is tranformed to create other members in a family of functions. All of the known Parent Functions are located in the "Common Functions & Their Parents" section below. There are two important concepts that go along with parent functions: The parent function of all parent functions is y = 0. This is a constant function, like y = 2.
# Common Functions & Their Parents:
Parent function of Parent functions: y = 0
Linear Function: y = 2x - 1
Parent Function: y = x
Quadratic Function: y = 2x² - 4x
Parent Function: y = x²
Cubic Function: y = x³ + 2x
Parent Function: y = x³
Radical Function: y = √x + 4
Parent Function: y = √x
Reciprocal Function: y = (1/x) + 3
Parent Function: y = (1/x)
Absolute Value Function: y = |x| - 2
Parent Function: y = |x|
# Rule 99. As remembered from the first rules of Algebra 2, transformations are the changed in terms of movement on the graph an equation has in relation to the parent function.
Horizontal and Vertical Translations remain pretty uniform throughout all the different types of functions. Vertical is f(x) + k, regular in that + k is up and -k is down. Horizontal is f(x - h), and is opposite, so f(x - h) is Right and f(x + h) is Left.
This carries on everywhere, for example in Absolute Value functions, f(x) = |x + 3| is a vertical translation. The absolute function in particular is special in that it is always a positive number:
When there is a negative for any function, it goes opposite whatever axis it is situated, mostly the Y-axis. The steps of tranformation are fairly simple, 3 to the left, 4 down, and reflected across the Y-axis if a is negative.
# Horizontal Vertical Translations:
Vertical: f(x) + k, regular
f(x) - k = down, f(x) + k = up
Horizontal: f(x - h), opposite
f(x - h) = Right, f(x + h) = Left
# Rule 100!. :)
Function Operations and Compositions are special ways to dense using f(x) and g(x) to act on eachother in some way. For example:
(f + g)(x) = f(x) + g(x): Sum
(f - g)(x) = f(x) - g(x): Difference
(f · g)(x) = f(x) · g(x): Product
(f / g)(x) = f(x) / g(x): Quotient
Of course, f(x) and g(x) are already given by the question. Operations can also be used to find domain. Also, you can input any number for x to find an absolute number, such as (f · g)(-6).
# Rule 101. There is one last thing known as a composition, or (f ∘ g)(x) = f(g(x)): Composition.
Again, you plug in any number for x, or not. You first find what g(x) is and thereafter find the value of f(x) with x being whatever value have been gotten from g(x). Simply put: empty circle in f ∘ g means f of g. Filled is multiply. If the result has radical x, the domain is [0, ∞), with whatever changes made, like √x - 2 as extra: [2, ∞).
# Rule 102. As long as the radical is greater or equal to whatever value is the minimum possible in the radical, in the case of Rule 101 negative two, it is a function. Parabolas will always have the domain of (-∞, ∞), as they go forever, containing all x-values. Same for cubic equations. Only when = 0 because of factoring are the values of x not part of the domain. If you have a reciprocal function where x is the denominator, 1/x, 0 must always be excluded: (-∞, 0) ∪ (0, ∞).
# Rule 103. Remember that Radicals multiply like normal: √x + 8 · √x + 5 = √x² + 13x + 40.
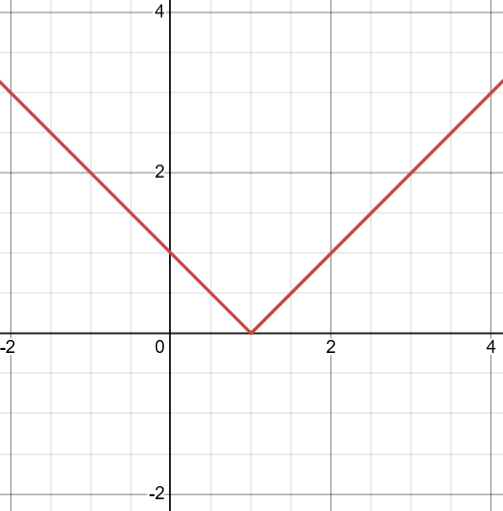
# Rule 104. Function f inverse = f⁻¹. Only if the function passes the Horizontal Line Test can it have an inverse. Only if it passes the Vertical Line Test can it be a function. For an equation like y = |x - 1|, which has the following graph:
In this graph, and the function it represents, there is no inverse because it does not pass the HLT. It is good to memorize the graphs of all the base parent functions, which are located in the "Common Functions & Their Parents" section further above. The inverse of f(x) is f⁻¹(x).
# Rule 105. The Domain of x is the Range of f⁻¹(x), while the Range of x is the Domain of f⁻¹(x). This is shown by this chart:
~~~
It was at this point I ceased writing rules for Precalculus, since my taking of Precalculus ran concurrent to my, which assumed a greater priority. The notes below, the WoO notes, are the rules and notes taken after the fact, years after I originally took the course. Though the notes above were taken during my Precalculus class itself, those below were taken after I had taken Calculus, and thus have a more reflective view of the material than that of an individual who is taking it for the first time. These notes will be a noticably higher quality than the past notes. I intend to undergo full studies of my existing notes as time goes on to make elaborations and make general improvements, making the Human Knowledge project into a more accurate and fully-fledged curated library of scientific and mathematical knowledge.
~~~
# WoO 1.
