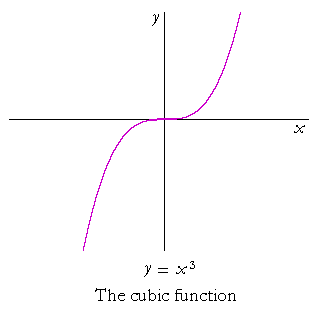These are my complete notes for Rules of Exponents in Algebra II.
I color-coded my notes according to their meaning - All numbered notes (which I call rules) are red, and include examples and the basis for understanding a topic. Definitions are written in green, and other important information (such as large-scale drawings that are better visualized than explained) was written in blue. All of this information is preserved on this page, with logical flow and breaks. I use ascii line drawings sparingly - If I can convey information or a graph using an image online, I will do so.
All of the knowledge present in these notes are filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Rules of Exponents (Algebra II)
VI. Rules of Exponents.
Rule 60. As with all other exponents, graphing Vertex form equations cubed has the same rules as when graphing them squared, where values inside the quantity (the parentheses) effect the x opposite to the sign (Rule 1), and values added/subtracted to the right being reflective to the y and applying as the sign states. Obviously, the shape of a cubed vertex form graph is different than that of a squared one. The basic curve of a cubed function (that is to say y = x³), is this:
Rule 61. To discover whether a function is even or odd (other than the nature of the leading coefficient) given that the function is a Polynomial, plug in -x for y and see what you get. For example, in the equation g(-x) = 3x² - 7, the x is substituted for 3x² - 7, which causes no change as the negative gets squared. As the equation is the same as before the substitution, the equation is even. A guide to determining Positivity/Negativity is below:
Opposite: Odd equation.
Result is...* Same: Even equation.
Half: Neither!
*compared to before substitution.
Don't ask what Neither means.
Generally the appearance of odd or even functions will follow the below format:
Rule 62. Cubic Functions are functions in which there are three X-method-esque values of x, such as (x - 2)(x + 3)(x + 4). The basic equation that these functions follow is f(x) = a(x - x1)(x - x2)(x - x3). In a basic equation where f(x) = (x + 4)(x - 3)(x - 6), with a being equal to 1 of course, the solutions would be x = -4, x = 3, and x = 6. The coordinates for this equation can be given as (-4 ,0), (3, 0), (6, 0), (0, 0), the final point being the y value that gets plugged in for f(x) so the solutions can be found. One group of coordinates that can be used to reverse create a cubic function is (-4, 0), (1, 0), (3, 0), (0, -6). Since the final point is a value for y, it must be plugged into the f(x) to get the value of a. Thus, the equation will become so: -6 = a(4)(-1)(-3). Plugging in the y point also plugs in zero for x. Simplifying leads to -1/2 = a, resulting in a finished product of f(x) = -1/2(x + 4)(x - 1)(x - 3)
Rule 63. Rational Exponents are essentially properties about how equations regarding exponents can be conducted. There are six main Holy Properties as it were, while the pt. 2 expansion of the properties contains another three. The first and most prevalent of the properties is the all-powerful:
1. am/n = n√aᵐ
- the universal property. When in doubt, try Holy Property #1. With this property, a sort of subproperty emerges stemming from how when m = 1, the equation just becomes n√a: Simply, a1/2 = √a. A constant rule that must be kept in mind for all of the properties is how the properties can be reversed depending on the equation and that transformation needing to be performed. For instance, √6 can just as easily be changed into 61/2 as it could be done the other way around. For an example of property #1, 644/3 = (∛64)⁴, which can be further simplified to (4)⁴, with a final answer of 256. One important thing to remember is how negative exponents just place the equation as the denominator in a fraction, for example 5-2/3 is just equal to (1 / 52/3), where nothing else can be done (Property #1 would render no further results). An example incorporating Property #1 is 16-5/4, where (1 / 165/4), = (1 / (∜16)⁵) = (1 / (2)⁵) = 1 / 32.
Rule 64. Continuation of Rule 59. While all "x = " equations with an even exponent create ± scenarios, double answers, Odd exponents only ever lead to direct answers, negative or positive depending on the original equation. For example, x³ = 64, and ∛64 only has one solution: 4. ∛-64, on the other side, also has but one answer, -4. An even exponent/index with a negative radicand, such as √-64, would lead to a complex answer, specifically 8i.
Rule 65. While for exponents on the same plane of existence that have coefficients being multiplied can simply be added (for example, exponents that are fractions must have their common denominators found to be added, 131/3 × 131/6 = 132/6 × 131/6 = 131/2), exponents on the outside of a parenthesis, such as (3⁵)⁶, have their exponents multiplied: 3³⁰. There are multiple planes of existence in which exponents or whatnot can appear: the first plane is within the parenthesis, the second is just outside, and the third is outside the brackets that enclose the previous two planes. For example, [(3⁵)⁶]³ is equivalent to (3³⁰)³, or 3⁹⁰.
Rule 66. The second rule of the holy properties is:
2. (ab)ᵐ = aᵐbᵐ
The more advanced brother of property #2 is property #3:
3. (aˣbʸ)ᵐ = aˣᵐbʸᵐ
An example of this is (51/5 × 81/3)⁵, which is equal to (51/5)⁵ × (81/3)⁵, where nothing else can be done. A good reversal of Property #2 can be seen in how 3² × 2² is equal to (6)². With x, Property #3 can still be conducted: (3x²)³ = 3³x⁶ = 27x⁶.
Rule 67. The Reason for why the exponent of 0 is equal to 1 in all circumstances is because of base-2: All descending powers of 2 are dividing by 2, ex. 2³ = 8, 2² = 4, and 2¹ = 2. Therefore, it would only make sense if it kept dividing by 2 after that, so 2⁰ = 1, 2⁻¹ = 1/2, 2⁻² = 1/4, and so on. For aesthetics.
Rule 68. Property #4:
4. (aᵐ) / (aⁿ) = aᵐ⁻ⁿ
This property is the only other completely unique property (in that it is not derived from any of the others) after Property #1, and I consider it the second most important property in terms of usage and all-encompassing nature. While Property #1 covers exponents that are fractions, Property #4 covers exponents within fractions. Of course, the scope of Property #4 is somewhat limmited due to the coefficients in both the numerator and denominators, a, need to be the same. The most simple example of the rule in action would be (4² / 4⁷) = 4⁻⁵, but a better, more intricate example incorporating Property #5:
5. (aᵐ / bᵐ) = (a / b)ᵐ
(which, upon first glance, may appear to be a spin on Property #4, but is really just another one of the Equivalence Properties) would be (561/4 / 81/4)³. Since the coefficients are different but the exponents are the same, Property #5 is used to create a multi-layered triple-plane equation: [(56/8)1/4]³. The internal fraction is easily divisible, removing a plane: (71/4)³. With simple multiplication the final answer of 73/4 is reached. Another equation specifically for Property #5 is (3x/2)⁴, which requires a reversal from the property. Applying the exponent to a, 3x, means to apply it to both the coefficient and the x: 3⁴x⁴, or 81x⁴. 2⁴ is 16, so the answer is 81x⁴ / 16.
Rule 69. Finally, Property #6:
6. n√a × n√b = n√ab
This property opens the rabbit hole into how square roots can be multiplied and divided, which has many subrules to remember. A simple example for the property is ∛4 × ∛128. Since too much mental power is require to ∛4 × 128, you can just factor 128 without multiplying:
128┃4
32┃4
8┃2
4┃2
2┃2
Thus, ∛4 × 4 × 4 × 2 × 2 × 2, including the unmultiplied 4, has two sets of triplets that can escape the cube root, 2 and 4, which multiply on the outside to make 8. Now, a fundamental rule that governs all the properties except perhaps for #1 and #4, is that exponents can be swapped out for roots and the property will still function. For example in Property #5, replacing m with n√ creates a child property to be remembered, (n√a) / (n√b) = n√(a / b). A good example of this is (5√192) / (5√6), which is turned to simply 5√192 / 6. Performing the internal division results in just 5√32, which is 2.
When there is a negative on the outside of the parentheses, swap the internal nominator and denominator and make the outer exponent positive. This may only be done when there is an outer left negative and where there is an outer right exponent that is negative as well.There is a reocurring role in fractions that there must never be a radical on the bottom and that if there ever is, it must be removed. This is done through mulitplication, like so:
2 × √3 2√3
━━ = ━━━
√3 × √3 3
Keep in mind that different radicals lead to different simplifications; take (∜19 / ∜4), for example. The first step is to multiply top and bottom by ∜4, in the same manner as shown above. However, in this case multiplying out the bottom will not make the denominator 4, as would be the case if it were a square root. Instead, as evident if actually multiplied out to ∜16, the result is 2 due to the heightened index/root, for a full answer of (∜76 / 2).
For odd indexes/roots, such as cubed roots, the complexity increases as the denominator can no longer be used to multiply out the bottom radical, it will have no effect. Therefore, another number must be found that will create a perfect cube in the denominator when multiplied. For example, (2 / ∛3) must be multiplied by a number that will turn the radical 3 into 27, the closest perfect cube that has a factor of 3. Therefore,
2 × ∛9 2∛9
━━━ = ━━━
∛3 × ∛9 3
The simple way for knowing how to multiply radicals and their coefficients as long as they have the same index/roots is through this example: (3√2)(5√3) = 15√6. As you can see, coefficients and radicals multiply separately.
Rule 70. The conjugate is a very useful tool for equations with a radical denominator with multiple unsimplifiable variables. The conjugate is, simply, the denominator with everything the same except for the sign in the middle. For example, the conjugate of √7 - 2 is √7 + 2. The conjugate of -3 - 2√5 is -3 + 2√5. Quite simply, the purpose of the conjugate is to multiply the nominator and denominator of one of these strange equations in order to remove the radical, the conjugate being just a special means to achieve that goal. For example, an actual equation in which the conjugate would be used is 1 / (√7 - 2), simple enough. Multiplying the conjugate is step one:
1 × (√7 + 2)
━━━━━━━━━
(√7 - 2) × (√7 + 2)
The bottom, after simplifying and cancellations, is equal to 3. The top, having been one, makes the answer simple: (√7 + 2) / 3.
Rule 71. When conducting an addition or subtraction equation between two radicals and their coefficients, try to simplify to make the radicals the same. In 5√12 - 19√3, simplifying √12 makes the first variable 10√3, which can be used in the equation to create -9√3. Simply put, not having the same radicand initially doesn't mean permanently.
Rule 72. The second part of the properties of radical equations is mainly just a summary of all the unusual side-effects of the properties from the first part. For example, the first side-effect is that for radicals where n√xⁿ, there are different possibilities for what x is equal to depending on whether n is odd or ever. This is due to negative numbers in even roots being taboo. If n is odd, then n√xⁿ = x, completely free no matter if x is negative or whatnot. ∛5³ = 5 and ∛(-5)³ = -5. Free country.
If n is even, however, then n√xⁿ = |x|, the absolute value of x, making it possible every time. ∜2⁴ = 2 and ∜(-2)⁴ = 2. 1984.
Keep in mind that when a letter variable like x is an even n equation, the absolute value symbols must remain with it in the answer: ∜x⁴ = |x|. Same internal exponent + same index = cancels out. When trying to create a n√xⁿ equation when the second n is greater, GCF the radicand to find something that will be able to be on the outside. Remember that when a variable that still has an exponent attached is spit out of an even n equation with an absolute value around it, such as |y⁴|, if the exponent is even, then the absolute value is to be removed as the exponent will cause it to be even either way. "Assume all variables are positive" relieves you of having to put abslute value. For the exponents of variables in the radicand, simplifying to see what you can't take out is as simple as dividing the exponent by the root, applying the result as the exponent of the variable on the outside, and using the remainder as the exponent of the variable on the inside.
Rule 73. This is just another means of simplification you've pretty much solved the equation: If a perfect square/whatnot must be left in its radical (∜4), you can square or whatever root it internally: ∜2². Optional.
Rule 74.
Not to be disclosed under ANY CIRCUMSTANCES!
If an internal Radicand is a perfect square and the index/root is even (∜1296), square root the radicand and divide the index by 2: √36. A Completely Legal move.
Rule 75. The second side-effect is another relating to fractions, but this is a bit of a tool to help you in solving variable and exponent packed equations. As you know, z⁻² = (1 / z²). As this logic would follow, (1 / z⁻²) = z². For example: (16xy1/3 / 8xz⁻⁴), the z can be moved to the top because it has a negative exponent in the denominator: (16xy1/3z⁴ / 8x).
Rule 76. (x² / x¹⁰) = (1 / x⁸). This is way faster than actually minusing 10 from 2 and going x⁻⁸ = (1 / x⁸). Just denominator exponent - nominator exponent.
One-to-one function: Any function that passes both the vertical and horizontal line test, e.g. it can have an inverse function.
Inverse Functions:
In an abstract sense, while a function is a relation between an input and an output such that there is only one output, the inverse function is taking the original and performing it in reverse order with the opposite operations. For example, if you have the function f(x) = 3x + 2, you are first multiplying by three and then adding by two. The inverse function would subtract by two and then divide by 3.
In a more practical sense, the inverse of the function is that in which the x and f(x) are reversed. For example, if you were to take this to be the output of the original function:
x ┃ y
━━╋━━
-2┃-4
-1┃-1
0┃2
1┃5
2┃8
Then this would be that of the inverse function:
x ┃ y⁻¹
━━╋━━
-4┃-2
-1┃-1
2┃0
5┃1
8┃2
How do you get the inverse function? Easily. ALl you have to do is take the original function, say y = (x / (x + 2)) and switch around y and x:
x = (y / (y + 2)). Then, all you have to do isolate y to find to find the inverse equation:
(y + 2) × (y / (y + 2)) = (y + 2) × (x)
y = xy + 2x
y - xy = 2x
y(1 - x) = 2x
y = 2x / (1 - x)
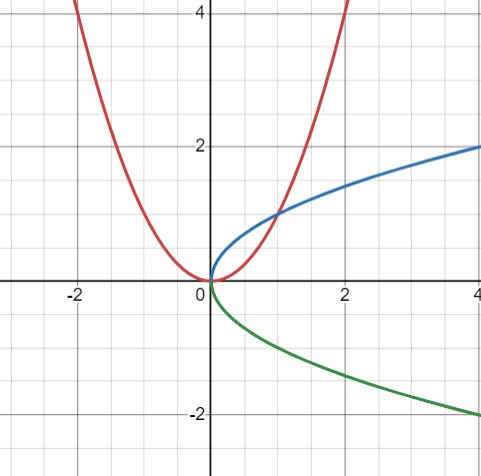
As we all know, a graph must pass the vertical line test in order to be considered a function. However, there is an additional horizontal line test that must be used to determine whether a function has an inverse. Take y = x², for example. This parabola clearly does not pass the horizontal line test, and so does not have an inverse in any official sense. However, if you were to switch around y and x and isolate y as you would for a regular inverse, you would find that the "inverse" is y = ±√x. However, as we know, this is not a 'real' inverse.
If there are five sections of the line for above and below zero, the degree is definitely even. Next, simply transcribe each segment of the graph as shown on the line:
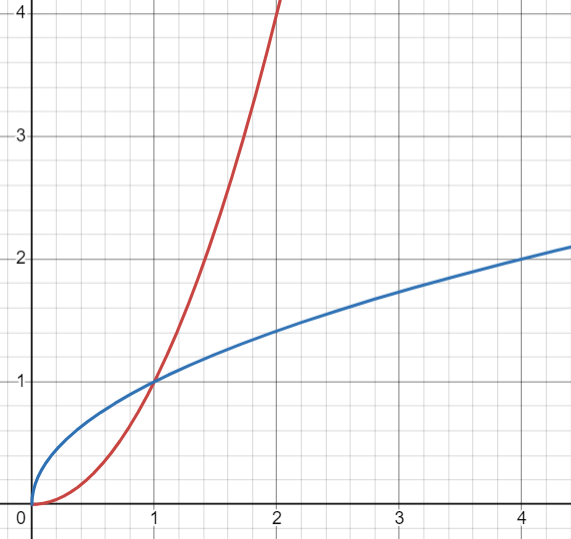
As you can see, y = x² does not pass the horizontal line test while the combined graph of ±√x does not pass the vertical line test. You cannot have an inverse function that is not a function, so x² does not have an inverse, because it is not a one-to-one function. However, we can create a restricted inverse function by creating restrictions upon the domain of y = x² and ±√x, x² being restricted to ≥ 0 while √x is restricted to y ≥ 0. This creates one-to-one functions in both functions, making them proper inverses of one another.
Note the symmetry of the restricted graph - inverse functions always mirror eachother along y = x.
In order to test whether two functions are inverses of one another, plug in and test these formulas to make sure they are true:
f(f⁻¹(x)) = x
f⁻¹(f(x)) = x
This is given any x value. Considering how the y values of f(x) are the x values of f⁻¹(x) and vice versa, this approach makes perfect sense.
Summary of Inverses:
-The domain of a function is the range of its inverse.
-The range of a function is the domain of its inverse.
-The inverse of a function is its reflection across the line y = x.
-Domain restrictions must be stated for inverse functions, because only one-to-one functions have inverses without domain restrictions!
NOTE: The inverse is not always the negative reciprocal. Negative Reciprocals are mainly used to find the slope of a line perpendicular to another, as described in rule [[[[[[[[[[[.
