These are my complete notes for Polynomial Functions in Algebra II (though notes that may relate to polynomial functions that are better included in a different section, such as in Quadratic Translation, Factoring, or any of the other sections of Algebra II may located there, so check the complete notes for anything you don't see in here.).
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Polynomial Functions (Algebra II)
III. Polynomial Functions.
# Intro to Polynomials:
An expression consisting of variables and coefficients that involves only addition, subtraction and multiplication, with non-negative integer exponents. x² - 2zx + 3y, x² + 3, and 1.33ˣ + 5x are all polynomials.
Some of the lower numbered Polynomial functions have names reflecting their highest degree, as shown in the section titled "Types of Polynomial Functions" (ctrl-f).
Anything involving a radical (any kind of root, square or otherwise) or negative exponent is inherently not a polynomial by not being either a non-negative number or a integer.
x⁶ - 2√x + 3x² - 5 is NOT a polynomial. There is a non-integer exponent.
x⁶ - √2x + 3x² - 5 IS a polynomial. Everything is correct.
# Types of Polynomial Functions:
Constant = f(x) = a₀ = f(x) = -14
Linear = f(x) = a₁x + a₀ = f(x) = 5x - 7
Quadratic = a₂x² + a₁x + a₀ = f(x) = 2x² + x - 9
Cubic = f(x) = a₃x³ + a₂x² + a₁x + a₀ = f(x) = x³ - x² + 3x
Quartic = f(x) = a₄x⁴ + a₃x³ + a₂x² + a₁x + a₀ = f(x) = x⁴ + 2x - 1
# Standard Form: Exponents are in descending order.
#
Rule .
Inequalities are Quadratic Equations that are not equal to 0 or y, but rather are >, <, ≥, ≤ to them. For the inequalities in terms of 0, an answer can be determined without the use of a graph, although the answer represents where the equation is true on the graph. The first thing to be done in an inequality-in-regard-to-zero type equation is to pretend that the equation is, in fact, equal to zero.
x² - 3x - 4 < x² - 3x - 4 = 0
Therefore, the Factoring X-Method can be done (see Rule 23). Create the double groupings, very important. (x - 4)(x + 1) < 0. x = 4, x = -1. Then to fully visualize the value of x (> 0 or < 0)
in relation to the X-intercepts found, make a number line with them:
<━━━━╋━━━━━━╋━━━>
-1 4
Then, plug in 0 for x in the double groupings you already created - (0 - 4)(0 + 1) < 0. See if the answer would be negative or not. plug in the sign of the answer to the part of the line where the number was plugged in, is:
+ - +
<━━━━╋━━━━━━╋━━━>
-1 4
There is a constant pattern of negative-positive-negative-positive, so every other section of the number line can be plugged in just from one known sign. Then, you must finally acknowledge whether the original question is less or greater to zero - this gives the answer. Based on the relationhship between the number line positive-negative pattern and the greater or lesser than nature of zero. If > 0, then you are looking for parts of the number line where it is positive and vice versa for < 0. This is the case even if there are ≥ 0 and ≤ 0 in play, just replicate that sign in the answer. If the space on the line graph where the 0 attribute (whether negative or positive) is contiguous and contained within one section, so can the answer: -1 < x < 4. The answer means to set the limits for the space in which x is true according to the equation. If the equation was ≤ 0, then the answer would be -1 ≤ x ≤ 4, little difference. If the space for where x is true is noncontiguous however, such as
+ - +
<━━━━╋━━━━━━╋━━━>
where x > 0, there is a special answer template. For the example if > , the answer would x < -1 OR x > 4. These are two separate equations unified as one answer. The x < _ or x > _ is the base template. X will always come first in the equation.
x² - 3x - 4 < x² - 3x - 4 = 0
Therefore, the Factoring X-Method can be done (see Rule 23). Create the double groupings, very important. (x - 4)(x + 1) < 0. x = 4, x = -1. Then to fully visualize the value of x (> 0 or < 0)
in relation to the X-intercepts found, make a number line with them:
<━━━━╋━━━━━━╋━━━>
-1 4
Then, plug in 0 for x in the double groupings you already created - (0 - 4)(0 + 1) < 0. See if the answer would be negative or not. plug in the sign of the answer to the part of the line where the number was plugged in, is:
+ - +
<━━━━╋━━━━━━╋━━━>
-1 4
There is a constant pattern of negative-positive-negative-positive, so every other section of the number line can be plugged in just from one known sign. Then, you must finally acknowledge whether the original question is less or greater to zero - this gives the answer. Based on the relationhship between the number line positive-negative pattern and the greater or lesser than nature of zero. If > 0, then you are looking for parts of the number line where it is positive and vice versa for < 0. This is the case even if there are ≥ 0 and ≤ 0 in play, just replicate that sign in the answer. If the space on the line graph where the 0 attribute (whether negative or positive) is contiguous and contained within one section, so can the answer: -1 < x < 4. The answer means to set the limits for the space in which x is true according to the equation. If the equation was ≤ 0, then the answer would be -1 ≤ x ≤ 4, little difference. If the space for where x is true is noncontiguous however, such as
+ - +
<━━━━╋━━━━━━╋━━━>
where x > 0, there is a special answer template. For the example if > , the answer would x < -1 OR x > 4. These are two separate equations unified as one answer. The x < _ or x > _ is the base template. X will always come first in the equation.
#
Rule .
when a questions uses the > 0 format on a number other than 0, such as 3x² - 13x + 10 > 0. Applicable anywhere. All the base algebraic properties, such as flipping the signs, still apply.
#
Rule .
For Quadratic Inequalities in which the equation is unequal to y or f(x), there are special answers regarding graphing. The methodry for finding the x-intercepts is the same as for 0-type inequalities (see Rule 37), but the way the graph is shown is the real way to convey what answers are true. The functions are summed up in the chart below (ALSO FIND Y-INTERCEPTS!):
The graphs of the four different quadratic inequalities, determined by greater than or lesser than symbols and if 'or equal to' is applied. Courtesy of Tiger Algebra.
If the line is linear, the same rules apply. y > means the area above the dotten line is true, while y < means the area below the line is true.
The graphs of the four different quadratic inequalities, determined by greater than or lesser than symbols and if 'or equal to' is applied. Courtesy of Tiger Algebra.
If the line is linear, the same rules apply. y > means the area above the dotten line is true, while y < means the area below the line is true.
#
Rule .
If there are multiple equations for y inequalities on the graph at the same time, such as y < -x² + 2x -3, then the space in which they overlap is the only true part of the graph:
Two inequalities that overlap in the graph. Courtesy of Dummies.
This is true even if a non-equal to equation (dotted line) is used.
Two inequalities that overlap in the graph. Courtesy of Dummies.
This is true even if a non-equal to equation (dotted line) is used.
#
Rule .
Any inequality for y or zero can be reversed in format by placing the variable at the front or the end. E.g., y > x² + 3 = x² + 3 < y. Reversing the 'than' sign is all that is needed.
# Degree: Highest exponent in an equation.
# Leading Coefficient: The coefficient with the highest degree attached.
#
Rule .
For equations involving xⁿ exponents, for Quadratic equations and those above with exponents higher than 2, there are two very important pieces of vocabulary: Degree and leading coefficient. To find these, first sort your Polynomial equation in a descending format, with the highest exponent coming first and so forth. This should be done in any circumstance. The degree is the highest exponent in the equation, the one that comes first. in x³ - x² + 3x, the degree is three. Secondly, the Leading Coefficient is the coefficient attached to the variable with the highest degree, at the very front of the equation. There are various names for equations with different highest degrees, to the third being Cubic,, to the fourth being Quartic, etc. A detailed template of the different types of equations can be seen in the Other Important information section "Types of Polynomial Functions" (ctrl-f). For these equations to be functions, the Base needs to be x-variable, with exponent n (> 0).
#
Rule .
There are several rules for Polynomial functions. For one, exponents cannot be negative - they can only be positive integers. 3ˣ, therefore, cannot be considered a polynomial. The base must be x for an exponent to be attached. To be a polynomial, the exponent has to be ≥ 0 integers. There are no rules for what the coefficients can be, only exponents and bases can have issues.
#
Rule .
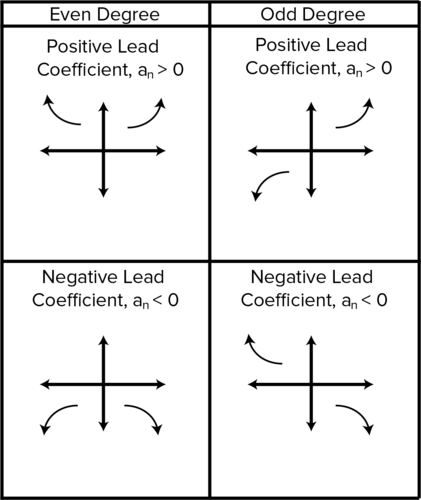
For all polynomial functions, the end behaviors (where x and y stretch out to infinity) can be quickly known from the knowledge of two factors: the degree and Leading Coefficient. Consult standard procedure (see Rule 42) as to whether the Degree is even or odd and whether the leading coefficient is negative or positive. An even coefficient creates a Parabola-Shaped graph and odd one creates a graph that increases concave-down to the origin, and the concave up increases to infinity. Negative and positive Leading Coefficients invert the graphs, turning the parabolar even graph upside down and the odd graph vice versa. For a more detailed chart, see the infographic titled "End Behavior of Polynomial Functions".
What is in the middle of the graph can only be determined by either
#1. the Decreasing/Increasing characteristics for y and x, or
#2. Plugging in numbers for x to find various coordinates. For #1, see Rule 45. For #2, see Rule 46. The end behavior of a Polynomial Function is representative of where x and y will progresss going into their respective infinities:
-, + ┃ +, +
━━━━━━╋━━━━━━
-, - ┃ +, -
What is in the middle of the graph can only be determined by either
#1. the Decreasing/Increasing characteristics for y and x, or
#2. Plugging in numbers for x to find various coordinates. For #1, see Rule 45. For #2, see Rule 46. The end behavior of a Polynomial Function is representative of where x and y will progresss going into their respective infinities:
-, + ┃ +, +
━━━━━━╋━━━━━━
-, - ┃ +, -
# End Behavior of Polynomial Functions:
The End Behaviors of Polynomial Functions, with acknowledgment of the center behavior being different depending on the exponent. Courtesy of Libretexts.
#
Rule .
When you get several lines of information stating where f(x) is increasing, decreasing, >0, and <0, you must convert this info into line chart form before it can be in Graph form. Example: f(x) is increasing when x < 0 and x > 4. This refers to continuity templates - see Rule 37. The line chart in this case would be:
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
For above/below zero: f(x) > 0 when -2 < x < 3 and x > 5. f(x) < 0 when x < -2 and 3 < x < 5. The line chart in this case would be:
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
The next step would be to place the lines on top of eachother accordingly:
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
If there are five sections of the line for above and below zero, the degree is definitely even. Next, simply transcribe each segment of the graph as shown on the line: The graph determined by the information gathered in this Rule.
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
For above/below zero: f(x) > 0 when -2 < x < 3 and x > 5. f(x) < 0 when x < -2 and 3 < x < 5. The line chart in this case would be:
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
The next step would be to place the lines on top of eachother accordingly:
Inc. Dec. Inc.
<━━━━━━━━━━━━━━╋━━━━━━━━━╋━━━━━━━━━━━>
0 4
Below Above Below Above
<━━━━━━━━━╋━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━>
-2 3 5
If there are five sections of the line for above and below zero, the degree is definitely even. Next, simply transcribe each segment of the graph as shown on the line: The graph determined by the information gathered in this Rule.
#
Rule .
This method for finding the middle section is relatively simple: just plug in various numbers for x in the equation to get coordinates. It is recommended to use all numbers -2 to 2, as that should be enough to create an accurate graph. More # can be used if necessary. Once the coordinates have been gotten, find the end behavior from the equation to make sure the coordinates are connected correctly. Plug in the coordinates to the graph and connect them correctly.
#
Rule .
When a question is asking to divide a from b, the question is asking for b ÷ a. This is the case for questions of the type in both subtraction and division. For Long Division, b goes outside the box whilst a goes inside: a b .
#
Rule .
For equations with three groups, such as (x + 2)(x - 1)(x - 3), multiply the first two equations first, and then multiply the result by the third group. Ex: (x² + x - 2)(x - 3). Further multiplied is x³ - 2x² - 5x + 6.