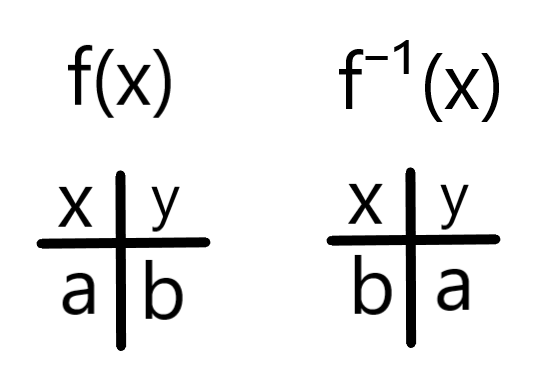These are my complete notes for Parents, Composition, and Inverse Functions in Precalculus, with the addition of Nonlinear Inequalities at the end.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Parents, Composition, and Inverse (Precalculus)
VIII. Parents, Composition, and Inverse.
# Rule 97. The Average Rate of Change is the slope of a line that passes through two points in a line, the slope of a secant line. This is a whole process, and at the end youg et to use a special formula:
(f(x₂) - f(x₁)) / (x₂ - x₁)
To perform the process, you need two bits of information: The point [x₁, x₂], and the equation.
First, keep in mind that [x₁, x₂] = (x₁, f(x₁)) and (x₂, f(x₂)). Then, simply go about plugging in the points in for x of the equation. For example, with the points [-2, -1] and the equation f(x) = -x³ + 3x, -2 would produce 2 and -1 would produce -2, creating the points of (-2, 2), (-1, -2). In plugging in these numbers to the formula, make sure to keep all negatives as the negatives in the formula can be subject to change, such as when f(x₂) or x₂ are negative. For this example, (-2 -2) / (-1 + 2) = -4/1, = -4.
You don't need to worry about if the points are both x or not, you just need to find f(x₁) and f(x₂) and plug them into the equation.
# Rule 98. Families of functions are groups of functions with graphs that display similar characteristics. The parent function is the skeleton key function, the simplest of functions in a family. It is the function that is tranformed to create other members in a family of functions. All of the known Parent Functions are located in the "Common Functions & Their Parents" section below. There are two important concepts that go along with parent functions: The parent function of all parent functions is y = 0. This is a constant function, like y = 2.
# Common Functions & Their Parents:
Parent function of Parent functions: y = 0
Linear Function: y = 2x - 1
Parent Function: y = x
Quadratic Function: y = 2x² - 4x
Parent Function: y = x²
Cubic Function: y = x³ + 2x
Parent Function: y = x³
Radical Function: y = √x + 4
Parent Function: y = √x
Reciprocal Function: y = (1/x) + 3
Parent Function: y = (1/x)
Absolute Value Function: y = |x| - 2
Parent Function: y = |x|
# Rule 99. As remembered from the first rules of Algebra 2, transformations are the changed in terms of movement on the graph an equation has in relation to the parent function.
Horizontal and Vertical Translations remain pretty uniform throughout all the different types of functions. Vertical is f(x) + k, regular in that + k is up and -k is down. Horizontal is f(x - h), and is opposite, so f(x - h) is Right and f(x + h) is Left.
This carries on everywhere, for example in Absolute Value functions, f(x) = |x + 3| is a vertical translation. The absolute function in particular is special in that it is always a positive number:
When there is a negative for any function, it goes opposite whatever axis it is situated, mostly the Y-axis. The steps of tranformation are fairly simple, 3 to the left, 4 down, and reflected across the Y-axis if a is negative.
# Horizontal Vertical Translations:
Vertical: f(x) + k, regular
f(x) - k = down, f(x) + k = up
Horizontal: f(x - h), opposite
f(x - h) = Right, f(x + h) = Left
# Rule 100!. :)
Function Operations and Compositions are special ways to dense using f(x) and g(x) to act on eachother in some way. For example:
(f + g)(x) = f(x) + g(x): Sum
(f - g)(x) = f(x) - g(x): Difference
(f · g)(x) = f(x) · g(x): Product
(f / g)(x) = f(x) / g(x): Quotient
Of course, f(x) and g(x) are already given by the question. Operations can also be used to find domain. Also, you can input any number for x to find an absolute number, such as (f · g)(-6).
# Rule 101. There is one last thing known as a composition, or (f ∘ g)(x) = f(g(x)): Composition.
Again, you plug in any number for x, or not. You first find what g(x) is and thereafter find the value of f(x) with x being whatever value have been gotten from g(x). Simply put: empty circle in f ∘ g means f of g. Filled is multiply. If the result has radical x, the domain is [0, ∞), with whatever changes made, like √x - 2 as extra: [2, ∞).
# Rule 102. As long as the radical is greater or equal to whatever value is the minimum possible in the radical, in the case of Rule 101 negative two, it is a function. Parabolas will always have the domain of (-∞, ∞), as they go forever, containing all x-values. Same for cubic equations. Only when = 0 because of factoring are the values of x not part of the domain. If you have a reciprocal function where x is the denominator, 1/x, 0 must always be excluded: (-∞, 0) ∪ (0, ∞).
# Rule 103. Remember that Radicals multiply like normal: √x + 8 · √x + 5 = √x² + 13x + 40.
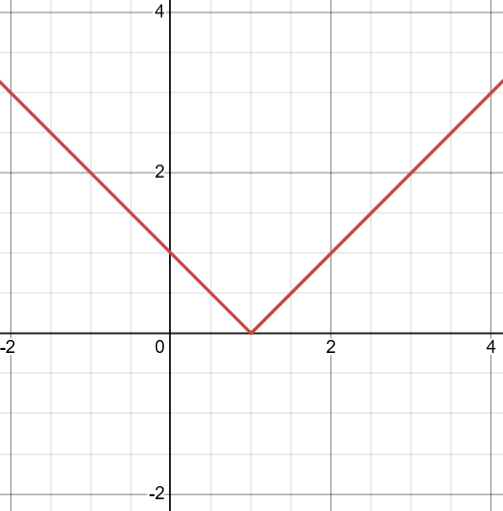
# Rule 104. Function f inverse = f⁻¹. Only if the function passes the Horizontal Line Test can it have an inverse. Only if it passes the Vertical Line Test can it be a function. For an equation like y = |x - 1|, which has the following graph:
In this graph, and the function it represents, there is no inverse because it does not pass the HLT. It is good to memorize the graphs of all the base parent functions, which are located in the "Common Functions & Their Parents" section further above. The inverse of f(x) is f⁻¹(x).
# Rule 105. The Domain of x is the Range of f⁻¹(x), while the Range of x is the Domain of f⁻¹(x). This is shown by this chart:
~~~
It was at this point I ceased writing rules for Precalculus in my notebook, as I had fallen behind in writing notes for past content and was busy with other schoolwork. This was prior to my creation of the more efficient rule-writing system that I would use in the future.
All notes below are WoO notes, explained here.
~~~
# WoO "105"-1: descriptor in bold. [This WoO does not necessarily bear any relation to Rule 105, it is just placed directly afterward.]
