# Rule . The derivative does not exist where the function does not. The tangent line at a point represents the slope of that point, as made possible by local linearity (see definition).

# Rule . To find at which point of a curve the tangent line is PARALLEL to another line, just find the derivative of the first line to get the slope of the tangent line. Then, just set that derivative equal to the slope of the 2nd line. To find when a tangent line is PERPENDICULAR to another line, do the same thing except set the first line derivative equal to the negative reciprocal of the 2nd line slope.

# Rule . In order to find the slope of a line that passes through the origin or any other point that is tangent to a curve, you have to set 2 equations equal to eachother.

First, for example, if y = ln(x/2) and the line passes through (0,0), the slope of the line at that point will equal:
$$\text{m} = \frac{ln(\frac{x}{2})-0}{x-0} = \frac{ln(x) - ln(2)}{x}$$ Secondly, find the derivative of the curve, which is (2/x) × (1/2) or 1/x.

Finally, you set the two equations equal to eachother:
$$\frac{1}{x} = \frac{ln(x) - ln(2)}{x}$$ 1 = ln(x) - ln(2)
ln(x) = 1 + ln(2)
e^ln(x) = e^{1 + ln(2)}
x = e × e^ln(2)
x = 2e
m = 1 / 2e

Remember to put the result back into the derivative of the equation at the end.

# Rule . To find the domain of a derivative, remember it conforms to the domain of the function as well. For example, if a vertical function is x ≠ 4 and x > 0, then the full domain is x > 0 and x ≠ 4.

# Rule . When there's an x in the base and the exponent, such as with y = x^x, you have to go the long way around with the ln (or log, if that's how you want to do it) to bring down the exponent and isolate x:

ln(y) = ln(x^x)
(1/y) × (dy/dx) = ln(x) + (x × 1/x)
(dy/dx) = y(ln(x) + 1)
(dy/dx) = x^x(ln(x) + 1)

The same sort of thing works with trigonometric functions in the exponent.

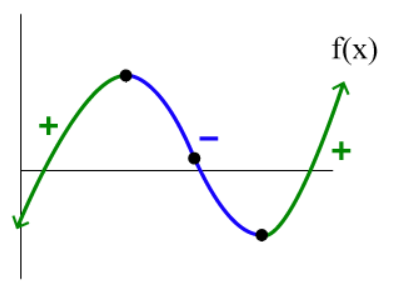
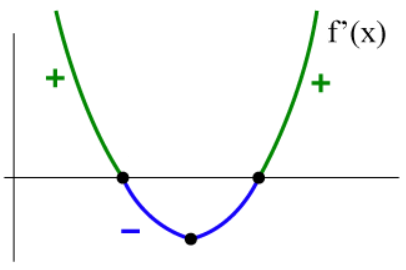
# Rule . Steps for determining the graph of a derivative:

First, find when the graph is flat, when the curve is parallel to the x-axis. These points will be the zeroes of the derivative graph.

Remember that the derivative graph represents the speed with which the slope of the function is changing, the rate of the rate of change.

For example, the derivative graph of:

The graph of a standard function, perhaps that of a polynomial. Courtesy of Calcworkshop.


Would be:

The graph of the derivative of the function given above. Courtesy of Calcworkshop.

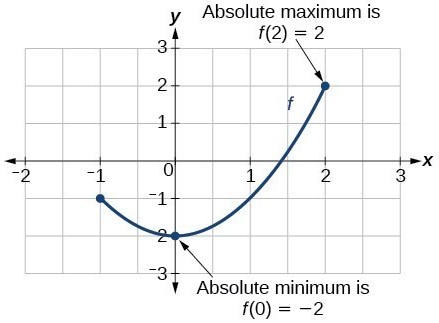
# Rule . Absolute (Global) Extreme Values:

Let f be a function with Domain "D". Then f(c) is the:

1. absolute maximum value on D if & only if f(x) ≤ f(c) for all x in D. Every y-value is less than particular y-value of f(c).



2. absolute minimum value on D if & only if f(x) ≥ f(c) for all x in D.

Examples of both Absolute Minimum and Maximum values can be seen below:

The Absolute Maximum and Absolute Minimum values for a restricted portion of a function. Courtesy of Lumen Learning.

# Rule . The Extreme Value Theorem:

If f is continuous on a closed interval [a, b], then f has both a minimum and a maximum value on the interval.

# Rule . Local Extreme Values:

Let c be an interior point on the domain of the function f. Then, f(c) is a:

1. local maximum value at c if & only if f(x) ≤ f(c) in the same interval containing c.



2. local minimum value at c if & only if f(x) ≥ f(c) in some open interval containing c.