Limits (Differential Calculus)

These are my complete notes for Limits in Differential Calculus.

I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.

# Average Rates/Speed: Average Speed is found by dividing the distance covered by the elapsed time.

# Limit: The value a function approaches as it becomes closer to a specified point - thus, not necessarily actually being at that point, but rather as close to it as possible with being on it. If a function is continuous near that point, the limit equals the function's value; otherwise, it will describe the behavior of the function even if undefined at that point.

# Properties of Limits:

Similar to Logarithms, Limits have their internal rules that can applied at any time. The "commandments" version of this list can be seen in Rule 110.

1. The limit of a constant is equal to a constant. $$\lim_{x \to a} c = c$$

2. The limit of x as x approaches a, equals a. $$\lim_{x \to a} x = a$$

3. The limit of a sum is the sum of the limits. $$\lim_{x \to a} (f(x) + g(x)) = \lim_{x \to a} f(x) + \lim_{x \to a} g(x)$$

4. The limit of a difference is the difference of the limits. $$\lim_{x \to a} (f(x) - g(x)) = \lim_{x \to a} f(x) - \lim_{x \to a} g(x)$$

5. The limit of a constant times a function is the constant times to limit of the function. $$\lim_{x \to a} [c × f(x)] = c \lim_{x \to a} f(x)$$

6. The limit of a product is the product of the limits. $$\lim_{x \to a} (f(x) × g(x)) = \lim_{x \to a} f(x) × \lim_{x \to a} g(x)$$

7. The limit of a quotient is the quotient of the limits, provided the denominator does not equal zero. $$\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}$$

8. The limit of a sum is the sum of the limits. $$\lim_{x \to a} (f(x))^n = (\lim_{x \to a} f(x))^n$$

# Rule 106. The average rate of change IS the slope. The average speed is the distance covered divided by the elapsed time, like miles per hour.

# Rule 107.Say that 16t² is the free fall motion of an object with no air resistance. It will follow the same (∆y / ∆t) formula as the slope formula.

∆ (Delta) means as "the change in", so (change in distance / change in time). From 0 to 2 seconds, the rock will travel (6(2)² - (6(0)^2)) / (2 - 0), or 34 ft/sec average speed.

# Rule 108. To find the instaneous speed/rate of change, the limit formula is as follows: $$\lim_{h \to 0} \frac{f(a + h) - f(a)}{h}$$ You know a and the equation at first, plug in (a + h) to the equation and complete formula. Then, plug in 0 for h to find instantaneous velocity/speed.

# Rule 109. Speed is the time rate at which an object is moving along a path, while velocity is the rate and direction of an object's movement.

# Rule 110. There are nine holy truths of limits that must always be remembered and and held immutable. They are similar to the mystical factoring rules, and some are versions of the Limit Properties referenced previously:

The equivalance of constants. (L.P. #1)

The equivalance of a to x approaching a. (L.P. #2)

The Sum Rule. (L.P. #3)

The Difference Rule. (L.P. #4)

The Constant Multiplication Rule. (L.P. #5)

The Limit Product Rule. (L.P. #6)

The Limit Quotient Rule. (L.P. #7)

The Limit Power Rule. (L.P. #8)

The Radical Rule. (a synthesis of L.P. #8 & #7 or #6)

# Rule 111. The one-sided limit is allowed to be infinity, while two-sided limits cannot be infinity and must not be a number.

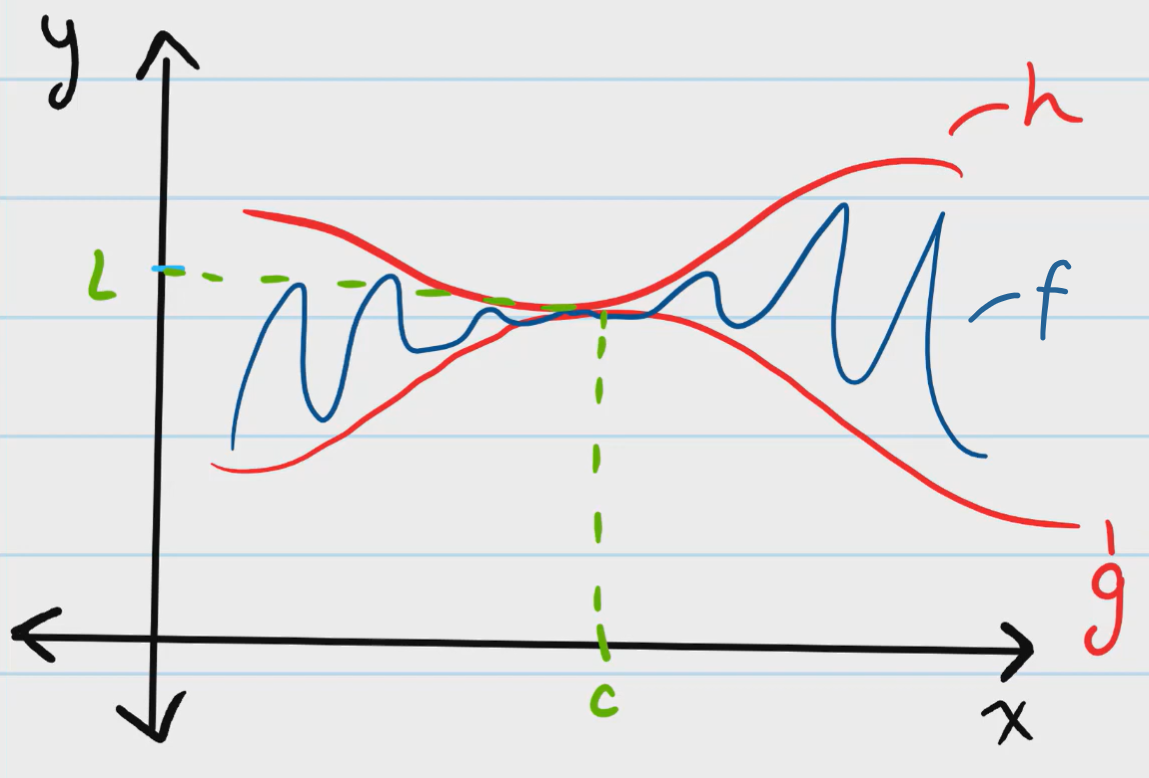
# Rule 112. The Squeeze Theorem:

When the limit can't be found directly, find it indirectly using the squeeze theorem. The way this theorem works, is to 'squeeze' function f (which has the uncertain limit) between two functions, h and g, and find their limits. Definitionally, this is written as follows:

If g(x) ≤ f(x) ≤ h(x), where x ≠ c in some interval around c, then: $$\lim_{x \to c} g(x) = \lim_{x \to c} h(x) = L$$
The classic example of a function that must use the Squeeze Theorem is one that oscillates, such as x² × sin(1/x).

$The demonstration of how the squeeze theorem may work on a function f, with the functions h and g above and below 'squeezing' the position of f at a point, thus requiring the limit of f to match that of h and g at that point. Courtesy of Cooper's Calculus.$

The demonstration of how the squeeze theorem may work on a function f, with the functions h and g above and below 'squeezing' the position of f at a point, thus requiring the limit of f to match that of h and g at that point. Courtesy of Cooper's Calculus.
The key idea of the Squeeze Theorem is that if h(x), which is above f(x), has its limit at c with the same y-value as g(x), then f(x) would also have to have that limit because it is between g(x) and h(x).

# Infinity/∞: The term 'infinity' does not refer - it describes the behavior of a function. Infinity means an increasing distance forever.

# Rule 113. The squeeze theorem also works for infinite limits.

# Rule 114. To find the horizontal asymptote, you can take the biggest thing on top, and divide it by the biggest thing on the bottom, or you could factor out the biggest base (with exponent), even if it makes every divisor weird. Then, factor to find the vertical asymptote, just plug in zero for the bottom, or cheat by using a graph.

# Rule 115. End Behavior Models

You can determine the end behavior of a complicated polynomial by looking at a similar one that acts exactly the same for extremely large values of x. For all polynomials, g(x) = a_n × xⁿ is the end behavior.

The function g must be:

a) A right end behavior model for f if $$\lim_{x \to ∞} \frac{f(x)}{g(x)} = 1$$

b) a left end behavior model for f if $$\lim_{x \to -∞} \frac{f(x)}{g(x)} = 1$$

# Rule 116. If the EBM is a constant, then it is a horizontal asymptote.

# Rule 117. A function's right & left end behavior models are not always the same function.

# Rule 118. Tradition dictates that for an equation with only two polynomials, the left one is the REBM and the right is the LEBM. Yes, opposite of what one may immediately think.

# Reciprocal Substitution:

There is a very specific and unique characteristic of Limits that must always be kept in mind when performing problems. Reciprocal substitution can be performed by taking the variable of the limit (90% of the time being x), flip it to its reciprocal (e.g., 1/x for x), and switch the term of the limit as shown below. This reciprocal is performed even for x's inside of trig. functions - it is done for all instances.

$$\lim_{x \to ∞} \frac{1}{x} = \lim_{x \to 0^+} x$$ $$\lim_{x \to -∞} \frac{1}{x} = \lim_{x \to 0^-} x$$
Infinity goes to Zero-Right, as Negative Infinity goes to Zero-Left. The nature of the reciprocal is not specific a specific side - either infinity or the zero could have 1/x or x.

# Rule 119. Rampant idiocracy has softened testing policy enough that you may be able to, in essence, cheat and look at the graph to determine values like the end behavior mode and asymptotes.

# Rule 120. If the assumed number for the LEDM of some two-polynomialed equation doesn't work, then try the answer for the REBM. Same for the issue vice-versa.

# Rule 121. For piecewise functions, even if x is ≥ or ≤ or > or whatever to 0, a (Lim x→0⁻) will make the function go to the f(x) for less than zero, and (Lim x→0⁺) makes it go to x > 0. Think of it like the plus and negative signs -0.1 or add 0.1 to the value.

Summary of Limits (Differential Calculus)

?. Limits.