# Rule . The derivative does not exist where the function does not. The tangent line at a point represents the slope of that point, as made possible by local linearity (see definition).

# Rule . To find at which point of a curve the tangent line is PARALLEL to another line, just find the derivative of the first line to get the slope of the tangent line. Then, just set that derivative equal to the slope of the 2nd line. To find when a tangent line is PERPENDICULAR to another line, do the same thing except set the first line derivative equal to the negative reciprocal of the 2nd line slope.

# Rule . In order to find the slope of a line that passes through the origin or any other point that is tangent to a curve, you have to set 2 equations equal to eachother.

First, for example, if y = ln(x/2) and the line passes through (0,0), the slope of the line at that point will equal:
$$\text{m} = \frac{ln(\frac{x}{2})-0}{x-0} = \frac{ln(x) - ln(2)}{x}$$ Secondly, find the derivative of the curve, which is (2/x) × (1/2) or 1/x.

Finally, you set the two equations equal to eachother:
$$\frac{1}{x} = \frac{ln(x) - ln(2)}{x}$$ 1 = ln(x) - ln(2)
ln(x) = 1 + ln(2)
e^ln(x) = e^{1 + ln(2)}
x = e × e^ln(2)
x = 2e
m = 1 / 2e

Remember to put the result back into the derivative of the equation at the end.

# Rule . To find the domain of a derivative, remember it conforms to the domain of the function as well. For example, if a vertical function is x ≠ 4 and x > 0, then the full domain is x > 0 and x ≠ 4.

# Rule . When there's an x in the base and the exponent, such as with y = x^x, you have to go the long way around with the ln (or log, if that's how you want to do it) to bring down the exponent and isolate x:

ln(y) = ln(x^x)
(1/y) × (dy/dx) = ln(x) + (x × 1/x)
(dy/dx) = y(ln(x) + 1)
(dy/dx) = x^x(ln(x) + 1)

The same sort of thing works with trigonometric functions in the exponent.

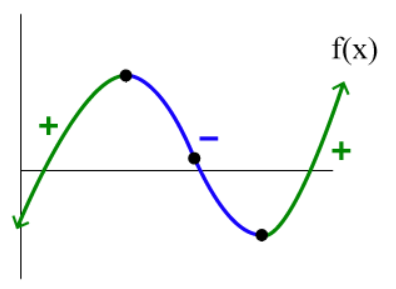
# Rule . Steps for determining the graph of a derivative:

First, find when the graph is flat, when the curve is parallel to the x-axis. These points will be the zeroes of the derivative graph.

Remember that the derivative graph represents the speed with which the slope of the function is changing, the rate of the rate of change.

For example, the derivative graph of:

The graph of a standard function, perhaps that of a polynomial. Courtesy of Calcworkshop.


Would be:

The graph of the derivative of the function given above. Courtesy of Calcworkshop.

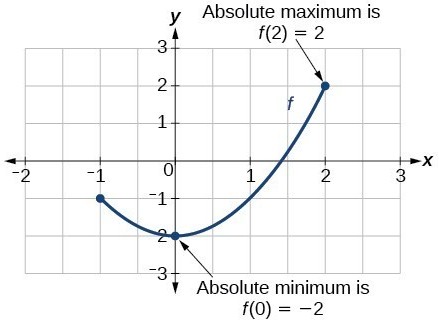
# Rule . Absolute (Global) Extreme Values:

Let f be a function with Domain "D". Then f(c) is the:

1. absolute maximum value on D if & only if f(x) ≤ f(c) for all x in D. Every y-value is less than particular y-value of f(c).



2. absolute minimum value on D if & only if f(x) ≥ f(c) for all x in D.

Examples of both Absolute Minimum and Maximum values can be seen below:

The Absolute Maximum and Absolute Minimum values for a restricted portion of a function. Courtesy of Lumen Learning.

# Rule . The Extreme Value Theorem:

If f is continuous on a closed interval [a, b], then f has both a minimum and a maximum value on the interval.

# Rule . Local Extreme Values:

Let c be an interior point on the domain of the function f. Then, f(c) is a:

1. local maximum value at c if & only if f(x) ≤ f(c) in the same interval containing c.



2. local minimum value at c if & only if f(x) ≥ f(c) in some open interval containing c.

# Rule . Individual Local Maxes (see Rule 172) can be created by restricting the domain, same with Local Minimums. They seriously work by just looking for the highest and lowest points on the position graph (if given).

The Global Max or Min. (see Rule 170) will be the highest or lowest within the graph itself. For situations in which the probable minimum or maximum number isn't on an exact x-value, it doesn't exist because you could get infinitely close to the open point value without actually getting there in a real number.

# Rule . Finding Extreme Values:

If a function has a local max or min. at an interior point c of its domain, and if f'(x) exists at c, then f'(c) = 0.

This is very obvious and should be childsplay to the novice mathematician.

# Rule . Critical Points:

The Critical Points of a function are the points (x-values) in which the function changes from increasing to decreasing or from decreasing to increasing. There are two ways to find these points: 1., by taking the derivative of the function and finding the points at which the derivative function equals to zero, and 2. by finding the points at which the derivative function equals DNE (e.g., where the denominator of a fraction equals zero).

The first way, setting the derivative of a function equal to zero, is relatively simple. Find the derivative of the function, and then set it equal to zero and isolate x. The 'zeroes' of the function, the values that, if plugged into the x of the derivative, will produce zero, are the x-values of the critical points. To find the y-values, plug in the found x-values into the function itself (the non-derivative, original function).

For the second way, critical points also exist where f'(x) = DNE, which algebraically generally just means that the denominator of the derivative equals zero, in circumstances in which the derivative is a fraction.

For an example of the first way:
f(x) = x³ - 3x² + 2
f'(x) = 3x² - 6x = 0
3x(x - 2) = 0

x = 0 & x = 2

Thus, where f'(x) = 0 & where f'(x) = DNE is where the critical points of a function reside.

# Rule . To find the Extrema Points, first plug in the endpoints to the function, make a line graph with endpoints and the Critical Points, and plug in the numbers in between to find whether the Critical Point is a maximum or minumum. The endpoints can be compared to find which is the global minimum/maximum and which is the local.

Plug in the #'s into the derivative function, and the Critical Points into the regular function.

Although a function's extreme points can only exist at a function's critical points or endpoints, not every critical point or endpoint signals the presence of an extreme value. If both sides of a critical point on a line graph are positive or negative, then the critical point is not a min or max.

# Rule . In quadratic fractions, the numerator determines the zeroes, and the denominator determines where the function is not defined.

# Rule . To find the derivative of a piecewise function, just take the derivative of the equations and keep the "x > 1" stuff the same. This can be used in the same pattern as the reuglar method seen in Rule 176.

# Rule . Mean Value Theorem:

If y = f(x) is continuous at every point of a closed interval [a, b] and differentiable at every point of its interval (a, b), then there is atleast one point c in (a, b) at which the instantaneous rate of change equals the mean rate of change:

$$f'(x) = \frac{f(b) - f(a)}{b - a}$$

# Rule . The way to show an equation satisfies the Mean Value Theorem is to first find the y-values for the endpoints of the interval and plug them into the slope formula (Rule 179): (f(b) - f(a)) / (b - a). Then, find the derivative of the equation and set it equal to the previously found value. If it is between the endpoints, it satisfied the Mean Value Theorem.