These are my complete notes for the Origin of Modern Astronomy.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Origin of Modern Astronomy
IV. Origin of Modern Astronomy.
# Modern Astronomy:
While Europe was going througn an anti-intellectual phase during the Middle Ages, there was a flowering of Astronomical discovery and progress during the Islamic Golden Age, which preserved and elaborated on the ideas of the Greeks. It was the end of the Dark Ages in Europe and the ushering in of the Renaissance that saw a revival in intellectual interest in sceintific, and importantly Astronomical, ideas in Europe. Copernicus embodied the spirit of European revival in interest in Astronomy (see below).
#
A. Rule .
Nicolaus Copernicus was a Polish astronomer who flourished during the early 1500s. He led the critical reappraisal of Ptolemy's ancient model of the Universe, which had stood as the dominant explanation of the cosmos for over a thousand years. He led the formation of the Heliocentric model of the solar system, which radically considered Earth itself to be a planet that orbited the sun, alongside all other planets. Additionally, he theorized that only the moon orbits the Earth.
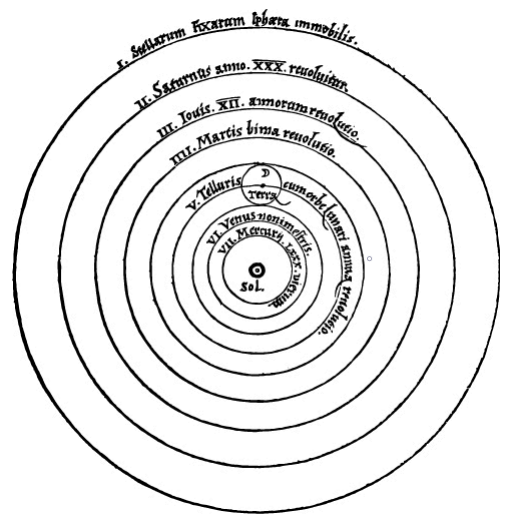
Copernicus developed a heliocentric plan of the solar system. This system was published in the first edition of De Revolutionibus Orbium Coelestium. Notice the word Sol for “Sun” in the middle.
As evident, he still assumed that the orbits of the planets would be uniformally circular. However, his ideas were revolutionary enough to provoke discussion across the scientific world, and the tenets of heliocentrism would eventually be popularly accepted over a century after his death. Controversially (as with everything he theorized), he explained the precession of the celestial sphere as being the result of the rotation of the Earth along its axis.
Copernicus developed a heliocentric plan of the solar system. This system was published in the first edition of De Revolutionibus Orbium Coelestium. Notice the word Sol for “Sun” in the middle.
As evident, he still assumed that the orbits of the planets would be uniformally circular. However, his ideas were revolutionary enough to provoke discussion across the scientific world, and the tenets of heliocentrism would eventually be popularly accepted over a century after his death. Controversially (as with everything he theorized), he explained the precession of the celestial sphere as being the result of the rotation of the Earth along its axis.
#
A. Rule .
Copernicus's masterpiece, De Revolutionibus, elaborates on Earth as one of six planets, and correctly lists the Planets in order of their proximity to the sun, and was able to deduce that the closer to the sun the planet, the greater the orbital speed.
Furthermore, complexities like retrograde motion were explained through this new theory with much simpler explanations than Ptolemy. This theory conflicted with the thousands of years of established common sense: the greek/classical schools of thought, and the dogma pushed by the Catholic Church.
Furthermore, complexities like retrograde motion were explained through this new theory with much simpler explanations than Ptolemy. This theory conflicted with the thousands of years of established common sense: the greek/classical schools of thought, and the dogma pushed by the Catholic Church.
#
A. Rule .
The scientific method, nonexistant during the time of Copernicus, was developed by Galileo Galileo during the 17th century. He greatly contributed to the understandings of Mechanics, Classical Physics of motion, and the influence of forces on bodies. Galileo theorized the basic principle of Inertia, that rest is no more natural a state for a body than motion. He argued that a force is required not only to start an object moving from rest, but also for slowing down, stopping, speeding up, and changing direction in any form. Additionally, in studying acceleration (see the acceleration definition), he found that objects will accelerate uniformly as they free fall or are otherwise influenced by gravity. These laws would be formulated in exact mathematical expressions.
Most importantly, he adopted the heliocentric model of the universe in the 1590s and began lecturing on the topic. The church pushed back, decreeing that heliocentrism was "false and absurd" in 1616 and disavowing its defense.
Galileo would drastically improve upon the telescope and its powers of magnification. He used this invention to observe the cosmos, beginning in 1609, and he discovered many distant stars too faint to be seen with the naked eye, and that the Milky Way across the night sky was made out of many stars as well.
He found that Jupiter had its own moons, circling Jupiter at different orbit speeds, proving that centers of motion could themselves be in motion (a theory argued against by geocentrics). Venus proved to go through phases like the moon, showing it revolved around the sun.
For these discoveries, Galileo was rewarded with a house arrest on the orders of the Catholic Church, who found his work heretical, and this would last until his death. In this confinement he would write one of his greatest masterpieces, the "Two New Sciences" which would form the foundations for modern Physics.
Most importantly, he adopted the heliocentric model of the universe in the 1590s and began lecturing on the topic. The church pushed back, decreeing that heliocentrism was "false and absurd" in 1616 and disavowing its defense.
Galileo would drastically improve upon the telescope and its powers of magnification. He used this invention to observe the cosmos, beginning in 1609, and he discovered many distant stars too faint to be seen with the naked eye, and that the Milky Way across the night sky was made out of many stars as well.
He found that Jupiter had its own moons, circling Jupiter at different orbit speeds, proving that centers of motion could themselves be in motion (a theory argued against by geocentrics). Venus proved to go through phases like the moon, showing it revolved around the sun.
For these discoveries, Galileo was rewarded with a house arrest on the orders of the Catholic Church, who found his work heretical, and this would last until his death. In this confinement he would write one of his greatest masterpieces, the "Two New Sciences" which would form the foundations for modern Physics.
#
A. Rule .
Tycho Brahe was a Danish astronomer who worked concurrent to Galileo, and produced a sound mathematical basis (along with Kepler) of Copernicus's Theory of Heliocentrism.
He established an observatory on a North Sea Island, and he is said to be the last of the pre-telescopic observers in Europe. He took extremely detailed records of the positions of the Sun, Moon, and Planets for almost 20 years, the greatest collection of such data since Hipparchus.
When he fled Denmark because of all the enemies he'd accumulated, he became the court Astronomer in Prague, where he enlisted the help of the young Astronomer Johannes Kepler in analyzing the data (see below).
He established an observatory on a North Sea Island, and he is said to be the last of the pre-telescopic observers in Europe. He took extremely detailed records of the positions of the Sun, Moon, and Planets for almost 20 years, the greatest collection of such data since Hipparchus.
When he fled Denmark because of all the enemies he'd accumulated, he became the court Astronomer in Prague, where he enlisted the help of the young Astronomer Johannes Kepler in analyzing the data (see below).
#
A. Rule .
Johannes Kepler was a German astronomer who served as Tycho Brahe's assistant in Prague. It was only after Brahe's death did Kepler gain access to the entirety of the records, which occupied him for the next 20 years. In this analysis, he developed three laws that dictate the motion of planets through Space, known as Kepler's Laws of Planetary Motion.
Law of Planetary Motion #1 - The Orbit of a planet is an ellipse with the Sun at one of the two foci.
Explanation: The path of an object through space is called its orbit. Kepler assumed, at first, that the orbits of planets were circles, but doing so only produced orbits that were consistent with Brahe's observations. He discovered that the orbit of Mars was elliptical rather than circular.
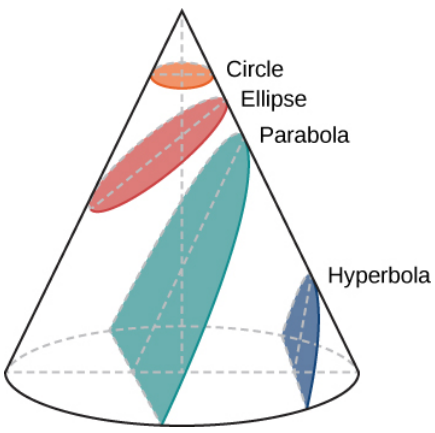
All of these shapes are closed curves, belonging to a family of curves known as conic sections.
The circle, ellipse, parabola, and hyperbola are all formed by the intersection of a plane with a cone. This is why such curves are called conic sections.
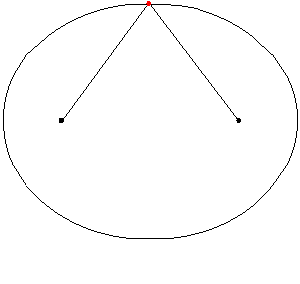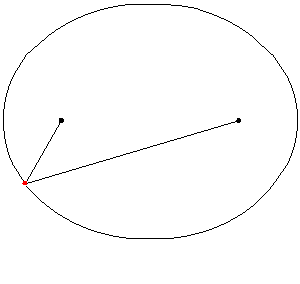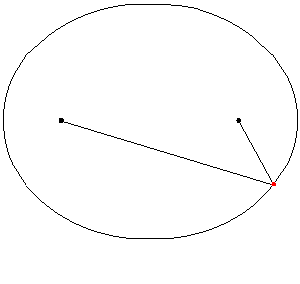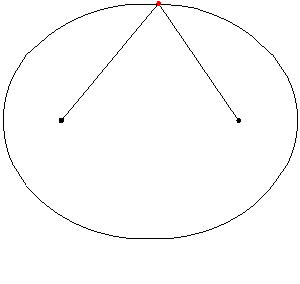
The center of a circle, of course, is a special point: the distance from the center of a cicle to anywhere on the circle is always the same - that is the radius. In an ellipse there are TWO special points, known as the foci, or the focus points of the ellipse. The sum of the distance from the focus points to any position on the ellipse is always the same:
An animated ellipse to illustrate that the sum of the distances from a point to the foci is constant. Courtesy of the UTSA.
The foci will change their postion depending on the size/nature of the ellipse. The widest diameter of the ellipse is called its Major Axis, while half that distance, the distance from the center of the ellipse from end to end, is called the Semimajor Axis. The smallest diameter of the ellipse is the Minor Axis (of Symmetry), perpendicular to the Major Axis, and it has two semimajor axes at either side of the center as well:
The Major Axis – the longest diameter of an ellipse, each end point is called a vertex.
The Minor Axis – the shortest diameter of an ellipse, each end point is called a co-vertex.
The Semimajor Axis (a) – Half of the major axis.
The Semiminor Axis (b) – Half of the minor axis.
Eccentricity (e) – the distance between the two focal points, F1 and F2, divided by the length of the major axis.
ae – the distance between one of the focal points and the centre of the ellipse (the length of the Semimajor axis multiplied by the eccentricity). Courtesy of the Science & Math Zone.
The Semimajor axis of the orbit of Mars (also the planet's average distance from the Sun) is 228 million kilometers.
The shape/roundness of an ellipse depends on how close together the two foci are, compared with the Major Axis. The ratio of the distance between the foci to the length of the major axis is called the Eccentricity of the ellipse. If the eccentricity is zero, then the foci will be in the same spot and the ellipse will be a circle. Thus, in elliptical terms, a circle is an ellipse of zero eccentricity with the Semimajor axis as the radius.
The greater the eccentricity, the more elongated the ellipse, up to a maximum eccentricity of 1.0, which is just a flat line. The size and shape of an ellipse are completely specified by its Semimajor axis and its Eccentricity. Mars has an elliptical orbit of 0.1, with the sun at one of the foci, the other being empty. This discovery was generalized by Kepler to apply to all orbits, with different eccentricities.
Law of Planetary Motion #1 - The Orbit of a planet is an ellipse with the Sun at one of the two foci.
Explanation: The path of an object through space is called its orbit. Kepler assumed, at first, that the orbits of planets were circles, but doing so only produced orbits that were consistent with Brahe's observations. He discovered that the orbit of Mars was elliptical rather than circular.
All of these shapes are closed curves, belonging to a family of curves known as conic sections.
The circle, ellipse, parabola, and hyperbola are all formed by the intersection of a plane with a cone. This is why such curves are called conic sections.
The center of a circle, of course, is a special point: the distance from the center of a cicle to anywhere on the circle is always the same - that is the radius. In an ellipse there are TWO special points, known as the foci, or the focus points of the ellipse. The sum of the distance from the focus points to any position on the ellipse is always the same:
An animated ellipse to illustrate that the sum of the distances from a point to the foci is constant. Courtesy of the UTSA.
The foci will change their postion depending on the size/nature of the ellipse. The widest diameter of the ellipse is called its Major Axis, while half that distance, the distance from the center of the ellipse from end to end, is called the Semimajor Axis. The smallest diameter of the ellipse is the Minor Axis (of Symmetry), perpendicular to the Major Axis, and it has two semimajor axes at either side of the center as well:
The Major Axis – the longest diameter of an ellipse, each end point is called a vertex.
The Minor Axis – the shortest diameter of an ellipse, each end point is called a co-vertex.
The Semimajor Axis (a) – Half of the major axis.
The Semiminor Axis (b) – Half of the minor axis.
Eccentricity (e) – the distance between the two focal points, F1 and F2, divided by the length of the major axis.
ae – the distance between one of the focal points and the centre of the ellipse (the length of the Semimajor axis multiplied by the eccentricity). Courtesy of the Science & Math Zone.
The Semimajor axis of the orbit of Mars (also the planet's average distance from the Sun) is 228 million kilometers.
The shape/roundness of an ellipse depends on how close together the two foci are, compared with the Major Axis. The ratio of the distance between the foci to the length of the major axis is called the Eccentricity of the ellipse. If the eccentricity is zero, then the foci will be in the same spot and the ellipse will be a circle. Thus, in elliptical terms, a circle is an ellipse of zero eccentricity with the Semimajor axis as the radius.
The greater the eccentricity, the more elongated the ellipse, up to a maximum eccentricity of 1.0, which is just a flat line. The size and shape of an ellipse are completely specified by its Semimajor axis and its Eccentricity. Mars has an elliptical orbit of 0.1, with the sun at one of the foci, the other being empty. This discovery was generalized by Kepler to apply to all orbits, with different eccentricities.
#
A. Rule .
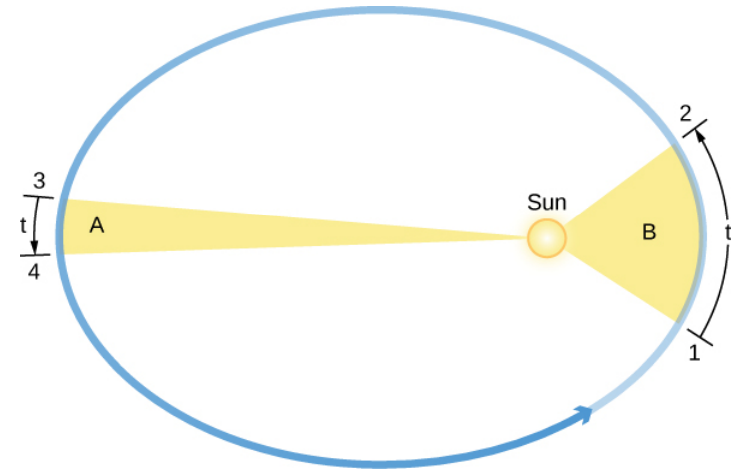
Law of Planetary Motion #2 - A line segment joining a planet and the sun sweeps out equal areas during equal intervals of time.
The 2nd Law deals with orbital speed, or the speed with which each planet moves along its ellipse. Kepler determined that Mars moves faster as it comes closer to the Sun, and slows down as it pulls away from the Sun.
Visualize an elastic band connecting a celestial body with the Sun. As the body gets farther from the sun, the band gets stretched, and thus moves slower until the band will pull it back to the sun. When it is closer to the sun, the band is not stretched as much and thus moves rapidly. Additionally, if you were to imagine the area sweeped in the ellipse (centered from the sun) by the orbit, then, given equal intervals of time, any two sweeped areas of the orbit will be equal.
The orbital speed of a planet traveling around the Sun (the circular object inside the ellipse) varies in such a way that in equal intervals of time (t), a line between the Sun and a planet sweeps out equal areas (A and B). Note that the eccentricities of the planets’ orbits in the solar system are substantially less than shown here.
While a circular orbit would cause a planet to move at the same speed throughout its orbit, the differing speeds of the planets as they move make it evident that their orbits are elliptical.
Law of Planetary Motion #2 - A line segment joining a planet and the sun sweeps out equal areas during equal intervals of time.
The 2nd Law deals with orbital speed, or the speed with which each planet moves along its ellipse. Kepler determined that Mars moves faster as it comes closer to the Sun, and slows down as it pulls away from the Sun.
Visualize an elastic band connecting a celestial body with the Sun. As the body gets farther from the sun, the band gets stretched, and thus moves slower until the band will pull it back to the sun. When it is closer to the sun, the band is not stretched as much and thus moves rapidly. Additionally, if you were to imagine the area sweeped in the ellipse (centered from the sun) by the orbit, then, given equal intervals of time, any two sweeped areas of the orbit will be equal.
The orbital speed of a planet traveling around the Sun (the circular object inside the ellipse) varies in such a way that in equal intervals of time (t), a line between the Sun and a planet sweeps out equal areas (A and B). Note that the eccentricities of the planets’ orbits in the solar system are substantially less than shown here.
While a circular orbit would cause a planet to move at the same speed throughout its orbit, the differing speeds of the planets as they move make it evident that their orbits are elliptical.
# Kinematics: The Science of motion, such as Newton's & Kepler's Laws.
#
A. Rule .
Law of Planetary Motion #3 - The square of a planet's orbital period is proportional to the cube of the length of the Semimajor axis of its orbit.
While the first two laws deal largely with the shape and speeds of a planet's orbit, there was yet to be a mathematical model for the spacing of the planets and how they ended up in the positions/orbits they have.
It was Kepler's 1619 discovery of a basic relationship relating the orbits of the planets to their relative distance from the sun that a mathematical model governing planetary spacing was formed. The Orbital Period P is the time it takes a planet to travel once around the Sun, and the Semimajor axis of a planet's orbit is equivalent to its average distance from the sun. In mathematical terms, this law can be defined as the following:
a³ ∝ T²
a³ = (M1 + M2) × T²
a = Length of the Semimajor axis of the planet's orbit, measured in AU.
M1 = The mass of the object being orbited.
M2 = The mass of the planet.
T = The planet's orbital period, measured in years.
With regard to the Earth (and all other planets where years and AU are the given units), the sides of the formula are not only proportional, but equal. The Third Law of Planetary Motion applies for all objects orbiting the sun, and enables the determination of an objects relative distance from the Sun based on how long the Orbital Period is.
Since Mars has an orbital period of 1.88 years, the third law tells us that (1.88)² = a³, using years and AU as the units. Therefore, the Semimajor axis of Mars has a length of ∛3.53 AU, or 1.52 AU, thus orbiting farther from the Sun than Earth.
While the first two laws deal largely with the shape and speeds of a planet's orbit, there was yet to be a mathematical model for the spacing of the planets and how they ended up in the positions/orbits they have.
It was Kepler's 1619 discovery of a basic relationship relating the orbits of the planets to their relative distance from the sun that a mathematical model governing planetary spacing was formed. The Orbital Period P is the time it takes a planet to travel once around the Sun, and the Semimajor axis of a planet's orbit is equivalent to its average distance from the sun. In mathematical terms, this law can be defined as the following:
a³ ∝ T²
a³ = (M1 + M2) × T²
a = Length of the Semimajor axis of the planet's orbit, measured in AU.
M1 = The mass of the object being orbited.
M2 = The mass of the planet.
T = The planet's orbital period, measured in years.
With regard to the Earth (and all other planets where years and AU are the given units), the sides of the formula are not only proportional, but equal. The Third Law of Planetary Motion applies for all objects orbiting the sun, and enables the determination of an objects relative distance from the Sun based on how long the Orbital Period is.
Since Mars has an orbital period of 1.88 years, the third law tells us that (1.88)² = a³, using years and AU as the units. Therefore, the Semimajor axis of Mars has a length of ∛3.53 AU, or 1.52 AU, thus orbiting farther from the Sun than Earth.
#
A. Rule .
Kepler's laws are highly qualitative, as they only reflect rules of thumb that Kepler discerned about the planetary motion in the solar systems. The laws do not actually explain what forces of nature are causing the celestial body to act in the ways specified; that is what makes them 'Laws' (see video for reference).
It would be Isaac Newton who would form the sound mathematical framework that explained the observations and rules formulated by Galileo, Brahe, Kepler, and the rest. As a professor of Mathematics at Cambridge, Newton dedicated much of his time to pondering the cosmos and reality, and from this he developed special mathematical models/equations and laws to govern motion itself, the forces behind Kinematics. He wrote down his theories in a book called the Principia, in 1687, where he unleashed unto an unsuspecting public his three laws of motion:
Law of Motion #1: Every object will continue to be in a state of rest, or move at a constant speed in a straight line, until it is compelled to change by an outside force. The first law is just a restatement of one of Galileo's discoveries, called the Conservation of Momentum (see P. Subsection VIII.II). This law states that in the abscence of any outside influence, there is a measure of a body's motion, called its momentum, that remains unchanged.
The first law is also oftentimes called the Law of Inertia, where Inertia is the tendency of an object to resist a change in the state of motion (see the Physics reference). In other words, a stationary object will stay at rest while a moving object will keep moving until some force intervenes.
It would be Isaac Newton who would form the sound mathematical framework that explained the observations and rules formulated by Galileo, Brahe, Kepler, and the rest. As a professor of Mathematics at Cambridge, Newton dedicated much of his time to pondering the cosmos and reality, and from this he developed special mathematical models/equations and laws to govern motion itself, the forces behind Kinematics. He wrote down his theories in a book called the Principia, in 1687, where he unleashed unto an unsuspecting public his three laws of motion:
Law of Motion #1: Every object will continue to be in a state of rest, or move at a constant speed in a straight line, until it is compelled to change by an outside force. The first law is just a restatement of one of Galileo's discoveries, called the Conservation of Momentum (see P. Subsection VIII.II). This law states that in the abscence of any outside influence, there is a measure of a body's motion, called its momentum, that remains unchanged.
The first law is also oftentimes called the Law of Inertia, where Inertia is the tendency of an object to resist a change in the state of motion (see the Physics reference). In other words, a stationary object will stay at rest while a moving object will keep moving until some force intervenes.
#
A. Rule .
Momentum relies on three factors:
Momentum, referred to as variable p, can be expressed through the following equation: p = m × v, where m is the object's mass and v is the velocity at any point.
It is difficult to see Momentum and the First Law of Motion in action in the real world, because of how many forces are acting on a body at any one time, from Air Resistance to Electromagnetism. For example, while a ball rolling on the sidewalk will eventually be slowed down due to Rubbing Friction (see P. Rule 56 and below), but if that ball was moving in space (the "vacuum" in which the idealized equations of kinematics are best applicable), the friction is so minute and insignificant that it would continue coasting through space forever. Thus, momentum can change only under the action of an outside force, such as gravity.
- Speed, how fast an object moves (zero if stationary).
- The direction of the motion, whether using relative, cartesian, or cardinal directions.
- The mass of the body, a measure of the amount of matter in a body.
Momentum, referred to as variable p, can be expressed through the following equation: p = m × v, where m is the object's mass and v is the velocity at any point.
It is difficult to see Momentum and the First Law of Motion in action in the real world, because of how many forces are acting on a body at any one time, from Air Resistance to Electromagnetism. For example, while a ball rolling on the sidewalk will eventually be slowed down due to Rubbing Friction (see P. Rule 56 and below), but if that ball was moving in space (the "vacuum" in which the idealized equations of kinematics are best applicable), the friction is so minute and insignificant that it would continue coasting through space forever. Thus, momentum can change only under the action of an outside force, such as gravity.
#
A. Rule .
Law of Motion #2: The change of motion of a body is proportional to, and in the direction of, the force acting on it.
This law expresses force in terms of its ability to change momentum with time. A force, push or pull, has both direction and magnitude. When a force is applied to a body, the momentum changes in the direction of the applied force. This means that a force is required to change either the speed or the direction of a body, or both - to start it moving, to speed it up, to slow it down, to stop it, or to change its direction.
The rate of change in an object's velocity is called acceleration, and the second law states that the acceleration of a body is proportional to the force being applied to it.
For example: Imagine a table as a smooth, frictionless surface. If you were to push a book across it, it will speed up as long as you keep pushing it with a positive acceleration (or negative acceleration if you are pushing it backwards). The harder you push the book, the more it will speed up. How much an object will accelerate given a force is reliant on the mass of the object; if you pushed a pen on the table with the same force you pushed the book with, it would accelerate to a higher speed.
This law expresses force in terms of its ability to change momentum with time. A force, push or pull, has both direction and magnitude. When a force is applied to a body, the momentum changes in the direction of the applied force. This means that a force is required to change either the speed or the direction of a body, or both - to start it moving, to speed it up, to slow it down, to stop it, or to change its direction.
The rate of change in an object's velocity is called acceleration, and the second law states that the acceleration of a body is proportional to the force being applied to it.
For example: Imagine a table as a smooth, frictionless surface. If you were to push a book across it, it will speed up as long as you keep pushing it with a positive acceleration (or negative acceleration if you are pushing it backwards). The harder you push the book, the more it will speed up. How much an object will accelerate given a force is reliant on the mass of the object; if you pushed a pen on the table with the same force you pushed the book with, it would accelerate to a higher speed.
#
A. Rule .
Law of Motion #3: For every action, there is an equal and opposite reaction (or: the mutual actions of two bodies upon each other are always equal and act in opposite directions).
This law generalizes the first law in a way that also defines mass. Thus, if there were to be a car system of multiple oblects, isolated from external forces, the first law would stipulate that the total momentum of the objects would remain constant.
Any change of momentum in a system must be balanced by another change, equal in force and opposite in direction, so that the momentum of the entire system is not changed. In every situation, there is always a force pair governing the reactions between any two objects. When you fall from a tree, the force pair is you and the Earth, because the Earth is exerting the force of gravity attracting you to the Earth, while the Earth is accelerated by the student's pull. You do not notice the change in momentum of the Earth because of its huge mass, which measures the inertia of the object, the tendency of the object to resist acceleration.
The recoil from hitting a ball with a baseball is further proof of the third law.
This law generalizes the first law in a way that also defines mass. Thus, if there were to be a car system of multiple oblects, isolated from external forces, the first law would stipulate that the total momentum of the objects would remain constant.
Any change of momentum in a system must be balanced by another change, equal in force and opposite in direction, so that the momentum of the entire system is not changed. In every situation, there is always a force pair governing the reactions between any two objects. When you fall from a tree, the force pair is you and the Earth, because the Earth is exerting the force of gravity attracting you to the Earth, while the Earth is accelerated by the student's pull. You do not notice the change in momentum of the Earth because of its huge mass, which measures the inertia of the object, the tendency of the object to resist acceleration.
The recoil from hitting a ball with a baseball is further proof of the third law.
# Volume: The measurement of how much Physical space an object occupies. Measured in cubic units, like cm³ or liters.
# Density: Mass divided by volume. Common units include g/cm³.
#
A. Rule .
Angular Momentum is the measurement of the rotation of a body as it revolves around some fixed point, like a planet rotating around the Sun. Mathematically, the angular momentum of an object is the product of its mass, velocity, and distance from the fixed point (which isn't always the radius, as known from elliptical orbits). If these three values were to be constant, meaning that an object's motion takes places at a constant velocity at a fixed distance from the spin center, then the angular momentum is also constant.
Kepler's 2nd law is a result of the conservation of angular momentum. As a planet approaches the Sun on an elliptical orbit and the distance to the spin center decreases; the planet speeds up to conserve angular momentum. Similarly, when the planet is farther from the sun, it moves slower. When you spin on a swivel chair at the park, when you have your arms outstretched, you move slower, but when you bring your arms inward, you speed up.
Kepler's 2nd law is a result of the conservation of angular momentum. As a planet approaches the Sun on an elliptical orbit and the distance to the spin center decreases; the planet speeds up to conserve angular momentum. Similarly, when the planet is farther from the sun, it moves slower. When you spin on a swivel chair at the park, when you have your arms outstretched, you move slower, but when you bring your arms inward, you speed up.
#
A. Rule .
Because the planets move in ellipses instead of straight lines, they must have a force bending their paths: Gravity. The Earth's gravity extends to the moon, and in doing so produces the force required to curve the Moon’s path from a straight line and keep it in its orbit. Furthermore, the attractive force of the Sun keeps all of the planets in their orbits.
It was the Third law of motion that truly rocked the scientific world in its day, and it carried with it the implication that there was a Universal attraction among all bodies everywhere in space. This attraction both explains the falling of objects on Earth and the orbit of the planets. Thus, Newton formulated the law of Gravitational Attraction, establishing a proportionality between the gravitational force between two objects and the mass & distances of the objects:
Fg = (G × M1 × M2) / R²
Fg = The Gravitational attraction between two bodies.
G = The Universal Gravitational Constant, roughly 6.6743 x 10^-11.
M1 = The Mass of the first object.
M2 = The Mass of the second object.
R = The distance between the two objects.
Gravity is internal to the code of mass - it is a property that was specifically given a value in the source code of the Universe. No matter the distance between two objects, there will always be a gravitational pull between them, with the gravitational pull of different objects affecting objects millions of kilometers away, such as through smaller galaxies orbiting larger ones.
It was the Third law of motion that truly rocked the scientific world in its day, and it carried with it the implication that there was a Universal attraction among all bodies everywhere in space. This attraction both explains the falling of objects on Earth and the orbit of the planets. Thus, Newton formulated the law of Gravitational Attraction, establishing a proportionality between the gravitational force between two objects and the mass & distances of the objects:
Fg = (G × M1 × M2) / R²
Fg = The Gravitational attraction between two bodies.
G = The Universal Gravitational Constant, roughly 6.6743 x 10^-11.
M1 = The Mass of the first object.
M2 = The Mass of the second object.
R = The distance between the two objects.
Gravity is internal to the code of mass - it is a property that was specifically given a value in the source code of the Universe. No matter the distance between two objects, there will always be a gravitational pull between them, with the gravitational pull of different objects affecting objects millions of kilometers away, such as through smaller galaxies orbiting larger ones.
#
A. Rule .
Some points in the orbits of the planets (specifically those in our Solar System) have been assigned special names:
Perihelion: The point along the orbit of a planet in which it is closest to the sun, and thus moving the fastest. For moons and artificial satellites of the Earth, the equivalent term is perigee.
Aphelion: The point along the orbit in which the planet is farthest from the sun, and thus moving the slowest. For moons and artificial satellites of the Earth, the equivalent term is apogee.
Perihelion: The point along the orbit of a planet in which it is closest to the sun, and thus moving the fastest. For moons and artificial satellites of the Earth, the equivalent term is perigee.
Aphelion: The point along the orbit in which the planet is farthest from the sun, and thus moving the slowest. For moons and artificial satellites of the Earth, the equivalent term is apogee.
#
A. Rule .
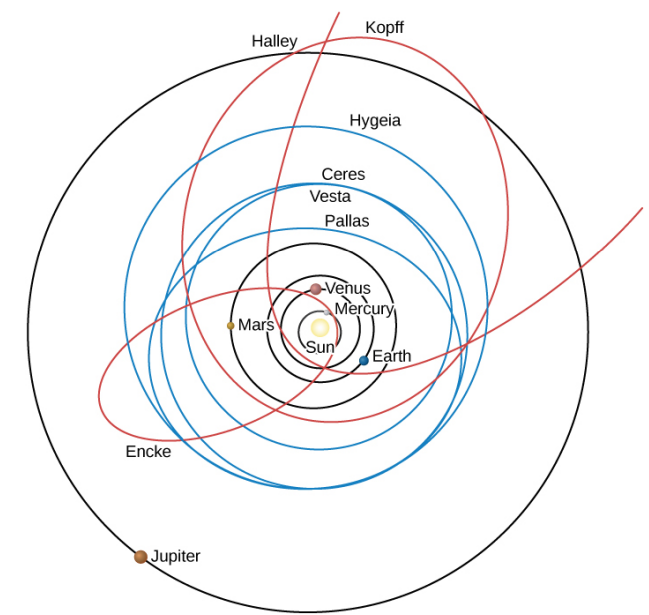
While the planets of the Solar System all tend to have low eccentricities (Mars has the largest, at 0.21), asteroids and comets (see Rule [[[ & Rule [[[ respectively) have their own trends in orbital eccentricities and other characteristics:
Generally, asteroids have smaller Semimajor axes in their orbits than comets, while comets have much larger orbits and eccentricities (averaging over 0.8). Most asteroids reside in the asteroid belt, a region between 2.2 & 3.3 AU, located in a gap between the orbits of Mars & Jupiter. The distance between Mars and Jupiter is large enough that a stable orbit of small bodies can exist in the gap.
The orbitals of various objects in the solar system. Black represents the five planets closest to the Sun, Red represents three comets, and Blue represents the four largest asteroids.
Generally, asteroids have smaller Semimajor axes in their orbits than comets, while comets have much larger orbits and eccentricities (averaging over 0.8). Most asteroids reside in the asteroid belt, a region between 2.2 & 3.3 AU, located in a gap between the orbits of Mars & Jupiter. The distance between Mars and Jupiter is large enough that a stable orbit of small bodies can exist in the gap.
The orbitals of various objects in the solar system. Black represents the five planets closest to the Sun, Red represents three comets, and Blue represents the four largest asteroids.
#
A. Rule .
When a satellite is in orbit, it does not need to exert any energy to remain in orbit. However, in order to get into orbit, the rocket that lifts the satellite into position must exert a huge amount of energy to accelerate it to Orbital Speed.
Furthermore, if it is the goal of the satellite to traverse beyond the orbit of Earth into further regions of the Solar System, then the rocket must reach Escape Speed, the speed needed to escape the pull of Earth. This is approximately 11 kilometers per second, and after escaping the orbit of the Earth, the satellite will simply be able to coast through space, interacting with nearby orbits as they pass by them, toward whichever target they intend. To avoid falling into these nearby orbits, small thruster rockets onboard must be used to adjust the trajectory.
Furthermore, if it is the goal of the satellite to traverse beyond the orbit of Earth into further regions of the Solar System, then the rocket must reach Escape Speed, the speed needed to escape the pull of Earth. This is approximately 11 kilometers per second, and after escaping the orbit of the Earth, the satellite will simply be able to coast through space, interacting with nearby orbits as they pass by them, toward whichever target they intend. To avoid falling into these nearby orbits, small thruster rockets onboard must be used to adjust the trajectory.
#
A. Rule .
Multiple Bodies:
The motion of a body under the gravitational influence of 2+ bodies complicates exponentially. Of course, every body is under the influence of everything in the universe all the time, but with increasing distance these influences becomes more negligible.
While when considering the effect of thousands of stars and bodies on eachother within a galaxy, it is clear that only extremely powerful supercomputers can compute the effects these bodies have on eachother (as they move) enough to predict their future locations.
Within the Solar System, things are much simpler, because the planets barely have any effect on the orbits of one another. These small influences are known as perturbations, and the study of their effects resulted in the discovery of Neptune in 1846.
The motion of a body under the gravitational influence of 2+ bodies complicates exponentially. Of course, every body is under the influence of everything in the universe all the time, but with increasing distance these influences becomes more negligible.
While when considering the effect of thousands of stars and bodies on eachother within a galaxy, it is clear that only extremely powerful supercomputers can compute the effects these bodies have on eachother (as they move) enough to predict their future locations.
Within the Solar System, things are much simpler, because the planets barely have any effect on the orbits of one another. These small influences are known as perturbations, and the study of their effects resulted in the discovery of Neptune in 1846.
#
A. Rule .
Discovering New Planets:
Uranus, the first planet discovered beyond those known to the ancients, was first noticed in 1781, by William Herschel. It had previously not been recognized as a planet, but as a star. This discovery proved that planets beyond those visible to the naked eye could exist, and that calculating the locations of these planets was possible.
The orbit of Uranus was calculated in 1790, using the observational data of the previous data. However, it was discovered that, even while accounting for the perturbations of the known planets, Uranus did not match the calculated orbit exactly - it was by 1840 that the discrepancy amounted to 0.03°, making it considerably larger than the pure error of margin in the orbital calculations.
To reconcile the difference in the position of Uranus with the Newtonian orbital formulas, an analysis of whether the irregularity could be caused by the pull of a new, previously unknown planet began. This research began in 1843 by John Couch Adams, and returned the mass, orbit, and approximate position for the planet in the sky.
Independently of one another, Adams and the frenchman Urbain Le Verrier both produced the mathematical deductions of the location and nature of the unknown planet, and it would be on September 23rd, 1846 that the planet was identified, confirming the generality of the Laws of Gravitation.
Uranus, the first planet discovered beyond those known to the ancients, was first noticed in 1781, by William Herschel. It had previously not been recognized as a planet, but as a star. This discovery proved that planets beyond those visible to the naked eye could exist, and that calculating the locations of these planets was possible.
The orbit of Uranus was calculated in 1790, using the observational data of the previous data. However, it was discovered that, even while accounting for the perturbations of the known planets, Uranus did not match the calculated orbit exactly - it was by 1840 that the discrepancy amounted to 0.03°, making it considerably larger than the pure error of margin in the orbital calculations.
To reconcile the difference in the position of Uranus with the Newtonian orbital formulas, an analysis of whether the irregularity could be caused by the pull of a new, previously unknown planet began. This research began in 1843 by John Couch Adams, and returned the mass, orbit, and approximate position for the planet in the sky.
Independently of one another, Adams and the frenchman Urbain Le Verrier both produced the mathematical deductions of the location and nature of the unknown planet, and it would be on September 23rd, 1846 that the planet was identified, confirming the generality of the Laws of Gravitation.
# Great Circle: Any circle on the surface of a sphere whose center is at the center of the sphere. For example, Earth’s equator is a great circle on Earth’s surface, halfway between the North and South Poles.
# Meridian: Any Great Circle that passes through both the north and south poles, perpendicular to the equator.
# Prime Meridian: The Meridian that serves as the longitude of 0°, passing through the Greenwich observatory in England.
# Longitude: The specific meridian a place on Earth is, measured in degrees (since the sphere is 360°) from the Prime Meridian. Numerically speaking, all lines of longitude west of the P.M. are referred to as "X Meridian West", with the same applied to all lines of longitude east of the P.M..
Each line of longitude in the West forms a great circle with another line in the East: "X Meridian West" is connected to the equivalent "180-X Meridian West".
# Latitude: Latitude is the y-axis analog to longitude - the number of degrees of arc away from the equator. Latitudes are measured either north or south of the equator from 0° to 90°, as the full horizontal Great Circle is counted as being the same latitude.
#
A. Rule .
There is a celestial version of the latitude and longitude system: Declination & Right Ascension. This system makes use of the space dome and the celestial equator.
Declination is the space equivalent to latitude, directed northward or southward from the celestial equator. Polaris, for example, has a declination of +90°.
Right Ascension is the space equivalent to longitude. However, instead of the Greenwich line, the arbitrary chosen line is the Vernal Equinox, the particular point in the sky in which the Ecliptic (the Sun's path) crosses the celestial equator.
Since the space dome can be seen turning around the Earth once a day as the planet turns on its axis, the Right ascension turns 360° in 24 hours, and thus each 15° of the arc is equivalent to 1 hour of time. For example, the celestial coordinates of the star Capella are R.A. 5h = 75° and declination +50°.
Declination is the space equivalent to latitude, directed northward or southward from the celestial equator. Polaris, for example, has a declination of +90°.
Right Ascension is the space equivalent to longitude. However, instead of the Greenwich line, the arbitrary chosen line is the Vernal Equinox, the particular point in the sky in which the Ecliptic (the Sun's path) crosses the celestial equator.
Since the space dome can be seen turning around the Earth once a day as the planet turns on its axis, the Right ascension turns 360° in 24 hours, and thus each 15° of the arc is equivalent to 1 hour of time. For example, the celestial coordinates of the star Capella are R.A. 5h = 75° and declination +50°.
#
A. Rule .
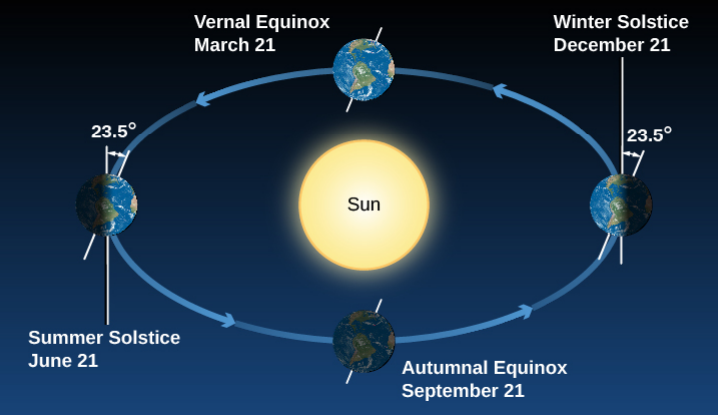
The Seasons:
Recall that the Earth is tilted on its axis by 23.5°, which is always in the same direction in space regardless of the point of the Earth in its orbit (see diagram).
As a result of the tilt of the Earth and the orbit around the Sun, during June the Northern Hemisphere is more directly facing the Sun, while the Southern Hemisphere is more directly facing it in December. These attributes are at their extremes on the Summer Solstice and the Winter Solstice, respectively.
During September and March, the Autumnal and Vernal Equinoxes respectively, the two hemispheres are equally favored with sunlight.
The Earth during different points of its orbit of the Sun, which results in different hemispheres being illuminated for different periods of time, resulting in the seasons.
Recall that the Earth is tilted on its axis by 23.5°, which is always in the same direction in space regardless of the point of the Earth in its orbit (see diagram).
As a result of the tilt of the Earth and the orbit around the Sun, during June the Northern Hemisphere is more directly facing the Sun, while the Southern Hemisphere is more directly facing it in December. These attributes are at their extremes on the Summer Solstice and the Winter Solstice, respectively.
During September and March, the Autumnal and Vernal Equinoxes respectively, the two hemispheres are equally favored with sunlight.
The Earth during different points of its orbit of the Sun, which results in different hemispheres being illuminated for different periods of time, resulting in the seasons.