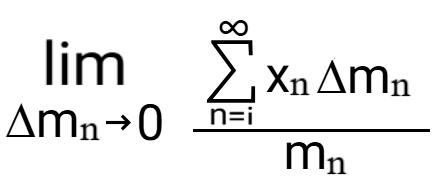This is the third part of my complete notes for Classical Mechanics, covering further topics of Dynamics such as Momentum, Center of Mass, Torque, and more. Due to the large scale of this topic, I have had to split even the complete notes into multiple parts.
I color-coded my notes according to their meaning - for a complete reference of each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Classical Mechanics, Part 3: Dynamics (cont.)
Table Of Contents
VIII. Momentum & Center of Mass
VIII.I Center of Mass.
#
P. Rule .
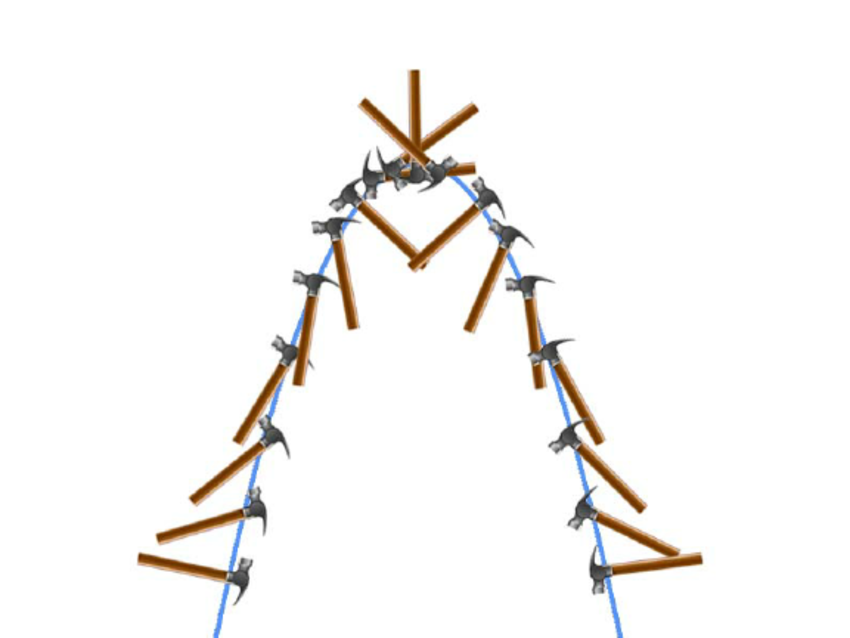
EVERYTHING moves in the parabolar shape as it is thrown in the air. The motion of irregularly shaped objects, like a hammer, seems to be much more complicated. However, you must see through the propaganda and see that the hammer rotates around its center of mass, and the motion of the center of mass of the hammer still follows a parabola just like a ball or something else with a symmetrical shape/constant density. Evidence:
Diagram of the dynamic motion of a hammer. The colored line represents the parabolic curve as the hammer falls under the influence of gravity.
Regardless of any rotation an object may be experiencing (as depicted with the hammer), you can consider the force of gravity to be acting directly on the center of mass. This holds true for all objects in projectile motion.
Diagram of the dynamic motion of a hammer. The colored line represents the parabolic curve as the hammer falls under the influence of gravity.
Regardless of any rotation an object may be experiencing (as depicted with the hammer), you can consider the force of gravity to be acting directly on the center of mass. This holds true for all objects in projectile motion.
#
P. Rule .
Expanding on the previous concept (see Rule 103), systems of objects also have their own center of mass (discerned through the location and individual masses/densities of all of the objects) that follows the same old parabolar projectile motion path. This is in spite of the fact that the balls are all moving relative to one another.
#
P. Rule .
When the object is in a constant gravitational field, the center of mass is the same as the center of gravity. We generalize Earth to have a constant gravitational acceleration (9.81 m/s²), even though that number actually varies at different locations on Earth (see Rule 14).
#
P. Rule .
The center of mass of an object is not necessarily always located on the object itself - think of a donut, for example. Constant density + constant shape = center of mass in the geometric center, regardless of if there is anything in the center.
#
P. Rule .
When you apply a force somewhere to the sides of the center of mass of the system, the applied force will rotate the system. If you apply a force to an object at, or directly toward, its center of mass (which is the case in practically every problem you will have to deal with), the force applied will not cause the object to rotationally accelerate - the force will only cause a linear acceleration of the object.
Note that even though many problems state that a force is pushing at an angle, 99% of the time that force is still being directed on the center of mass, just from a new angle of attack.
Note that even though many problems state that a force is pushing at an angle, 99% of the time that force is still being directed on the center of mass, just from a new angle of attack.
#
P. Rule .
When hung or tipped, the force of gravity will pull directly upon the center of mass of the object to bring the center of mass back to its lowest point. When you tip one of those untippable cups, the center of mass is getting raised in the air (because it was already very low), and so the force of gravity will naturally pull downward on the center of mass, as a result causing the cup to stand upright again.
#
P. Rule .
There is a trick you can use to determine the center of mass of a flat object in reality: simply hang the object up by one end and place tape vertically, from where the object is hung to the bottom. Then, turn the object and repeat the process. Where the two lines of tape intersect is where the enter of mass will be.
# Point Object/Point Particle: An object small enough that its size and shape are irrelevant - it can just be considered to be a dot in space, possibly with a mysterious mass associated with it as well.
# Centroid: The unweighted, geometric center of a system. If there are two objects in a system, and one is 1000x the mass of the second, the centroid will still be directly in the middle between them. Thus, the centroid is the ignoramus's center of mass.
#
P. Rule .
Calculating the center of mass of a system is lightwork. First, collect the mass and positions in the cartesian plane of each individual object of the system. This system works best with point objects. A general equation for the center of a system is flexible to work with any number of points, but must be solved separately for the x, y, and z directions of the points, as follows:
xcom = (Σ mnxn) / (Σ mn)
ycom = (Σ mnyn) / (Σ mn)
zcom = (Σ mnzn) / (Σ mn)
This equation is described variously as the "system of particles" equation, or simply the "particle system" equation. Each of the known "positions" of the particles are with respect to a zero reference point (usually the origin, though it can differ depending on the problem, requiring the individual to perform extra calculations).
A revolutionary, modern super-equation fit for the 21st century has recently been discovered to combined ALL THREE directions in three-dimensional space into a single, efficient, all-use equation. It is as follows:
rcom = (Σ mnrn) / (Σ mn)
Since r contains all three of the directions (xî + yĵ + zk̂), it returns the exact center of mass three-dimensionally.
Going further, as a true testament to the progress of science, scientists have discovered that taking the derivative of this super-equation will result in a system-velocity equation, which describes the velocity of the center of mass of a system of particles:
vcom = (Σ mnvn) / (Σ mn)
xcom = (Σ mnxn) / (Σ mn)
ycom = (Σ mnyn) / (Σ mn)
zcom = (Σ mnzn) / (Σ mn)
This equation is described variously as the "system of particles" equation, or simply the "particle system" equation. Each of the known "positions" of the particles are with respect to a zero reference point (usually the origin, though it can differ depending on the problem, requiring the individual to perform extra calculations).
A revolutionary, modern super-equation fit for the 21st century has recently been discovered to combined ALL THREE directions in three-dimensional space into a single, efficient, all-use equation. It is as follows:
rcom = (Σ mnrn) / (Σ mn)
Since r contains all three of the directions (xî + yĵ + zk̂), it returns the exact center of mass three-dimensionally.
Going further, as a true testament to the progress of science, scientists have discovered that taking the derivative of this super-equation will result in a system-velocity equation, which describes the velocity of the center of mass of a system of particles:
vcom = (Σ mnvn) / (Σ mn)
#
P. Rule .
In order to find the change in position of the center of mass of a system, you must use the center of mass equation for the initial position, and then for the final position, and subtract former from the ladder, in the delta "change in" tradition.
#
P. Rule .
One method of finding the center of mass of irregular objects is to split the object into multiple, normally shaped objects (like squares, rectangles, triangles, and other basic shapes) which can then be used in a 'system-of-particles'-type problem (see Rule 110).
#
P. Rule .
If you don't know mass in a problem with multiple objects, do not fear: When all the pieces of the object (or all of the parts of a system) have the same density and thickness, the center of mass equation can be altered as follows, utilizing area instead:
xcom = (A1x1 + A2x2 + ...) / (A1 + A2 + ...)
This is derived through the following means, with ρ being volumetric mass density:
ρ1 = ρ2
(m1 / ∀1) = (m2 / ∀2)
(m1 / (A1 × t)) = (m2 / (A2 × t))
(m1 / A1) = (m2 / A2)
m1 = (A1 / A2) × m2
From there, you can just plug in that value into the center of mass equation, causing every term to have the same mass. Thus, the mass can be canceled out, and now only the area of each object is needed to complete the problem.
xcom = (A1x1 + A2x2 + ...) / (A1 + A2 + ...)
This is derived through the following means, with ρ being volumetric mass density:
ρ1 = ρ2
(m1 / ∀1) = (m2 / ∀2)
(m1 / (A1 × t)) = (m2 / (A2 × t))
(m1 / A1) = (m2 / A2)
m1 = (A1 / A2) × m2
From there, you can just plug in that value into the center of mass equation, causing every term to have the same mass. Thus, the mass can be canceled out, and now only the area of each object is needed to complete the problem.
#
P. Rule .
If the object has a hole in it, you can calculate the center of mass by imagining the hole and the object it is part of as being separate particles, calculating the center of mass for each individually. From there, you can use the classic 'system of particles' equation (see Rule 110). However - be careful to instead SUBTRACT the terms relating to the hole in the equation instead of adding them, in order to account for the center of mass being shifted away from the part of the object with the hole.
# Uniform: When applied in the context of all of this center of mass nonsense, it means that the object has constant density.
#
P. Rule .
It is possible, more efficient, and fairly easy to use calculus in order to calculate the center of mass, deriving the equation for it from the density equation and the system of particles equation.
First, the summation of all of the particles in the system must be made to account for an infinite amount of particles, the mass of which will each approach zero as they get more numerous and more representative of actual particles. This can be represented as follows:
The integral for determining the center of mass of a system.
Each infinitesimally small particle can be called "dm", and the whole expression can be written as the following integral:
$$x_{cm} = \frac{1}{m_{\text{total}}} \int x \, dm$$
This is the universal equation for density, but note that finding what equality will turn dm into dx in the first step every time the equation is used. Determining the mass through whatever means necessary is also very important.
Basic example:
Assume a triangle with the thickness t and a uniform volumetric mass density p, with a base a and a height b. Since we cannot directly take the integral of x with respect to mass, we will first use the density equation to determine relationship between x-direction and mass. Since dm (each rectangle subdivision of the object) and the object itself have the same density,
ρ = (mtotal / Vtotal) = (dm / dV)
dm = ρdV
And now, since the volume of the dm box is equal to length × width × height, a new value for dV can also be determined.
dV = y × t × dx
Now,
dm = ρ × y × t × dx
From there, the original (mtotal / Vtotal) version of density can be recalled and fully expanded while being set equal to the fully fleshed out second side of the equation:
(mtotal / Vtotal) = (mtotal / ½abt) = (2mtotal / abt)
dm = ρ × y × t × dx
= (2mtotal / abt) × y × t × dx
=(2ymtotal / ab) × dx
FINALLY,
$$x_{cm} = \frac{1}{m_{\text{total}}} \int_0^a x \left( \frac{2ym_{\text{total}} }{ab} \right) \, dx$$
Moving out all of the constants, you get:
$$x_{cm} = \frac{2}{ab} \int_0^a xy \, dx$$ Still, the y must be replaced with something else in order to take the integral, and so the basic slope formula can be used for this purpose:
y = mx + y0
y = (b/a) × x
$$x_{cm} = \frac{2}{ab} \int_0^a x \left( \frac{b}{a} x \right) \, dx$$ =
$$x_{cm} = \frac{2}{a^2} \int_0^a x^2 \, dx$$
Solving this problem out, you get (2/3) × a.
First, the summation of all of the particles in the system must be made to account for an infinite amount of particles, the mass of which will each approach zero as they get more numerous and more representative of actual particles. This can be represented as follows:
The integral for determining the center of mass of a system.
Each infinitesimally small particle can be called "dm", and the whole expression can be written as the following integral:
$$x_{cm} = \frac{1}{m_{\text{total}}} \int x \, dm$$
This is the universal equation for density, but note that finding what equality will turn dm into dx in the first step every time the equation is used. Determining the mass through whatever means necessary is also very important.
Basic example:
Assume a triangle with the thickness t and a uniform volumetric mass density p, with a base a and a height b. Since we cannot directly take the integral of x with respect to mass, we will first use the density equation to determine relationship between x-direction and mass. Since dm (each rectangle subdivision of the object) and the object itself have the same density,
ρ = (mtotal / Vtotal) = (dm / dV)
dm = ρdV
And now, since the volume of the dm box is equal to length × width × height, a new value for dV can also be determined.
dV = y × t × dx
Now,
dm = ρ × y × t × dx
From there, the original (mtotal / Vtotal) version of density can be recalled and fully expanded while being set equal to the fully fleshed out second side of the equation:
(mtotal / Vtotal) = (mtotal / ½abt) = (2mtotal / abt)
dm = ρ × y × t × dx
= (2mtotal / abt) × y × t × dx
=(2ymtotal / ab) × dx
FINALLY,
$$x_{cm} = \frac{1}{m_{\text{total}}} \int_0^a x \left( \frac{2ym_{\text{total}} }{ab} \right) \, dx$$
Moving out all of the constants, you get:
$$x_{cm} = \frac{2}{ab} \int_0^a xy \, dx$$ Still, the y must be replaced with something else in order to take the integral, and so the basic slope formula can be used for this purpose:
y = mx + y0
y = (b/a) × x
$$x_{cm} = \frac{2}{ab} \int_0^a x \left( \frac{b}{a} x \right) \, dx$$ =
$$x_{cm} = \frac{2}{a^2} \int_0^a x^2 \, dx$$
Solving this problem out, you get (2/3) × a.
#
P. Rule .
Despite what you have been indoctrinated into believing in school, there are actually THREE (3) types of density relating to mass.
- Volumetric Mass Density: ρ = (m / V). Defined by Wikipedia as "a substance's mass per unit of volume". Note that there are actually other types of volumetric density, such as volumetric weight density & volumetric charge density.
- Surface Mass Density: σ = m / A.
- Linear Mass Density: λ = m / L. The amount of mass per unit length.
#
P. Rule .
Internal forces will occur when particles within the system collide with one another. However, those internal forces form a Newton's 3rd Law force pair and cancel one another out. Thus,
ΣFinternal = 0
Thus, even when a collisions occurs with the system, if there is no net external force acting on the system, the acceleration will be zero and thus the velocity (and linear momentum) of the center of mass of the system will remain constant.
ΣFinternal = 0
Thus, even when a collisions occurs with the system, if there is no net external force acting on the system, the acceleration will be zero and thus the velocity (and linear momentum) of the center of mass of the system will remain constant.
VIII.II Momentum Basics.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: p = m × v
p = Momentum.
m = Mass.
v = Velocity.
Definition: "Inertia in Motion", the property of an object in motion to remain in the state of motion. It is always in the same direction as the velocity.
Note that when you are calculating momentum, you calculate momentum in relation to the individual objects of a system, not forces. This is why in conservation of momentum you only include the objects of the system in your calculations.
# Momenta: The plural of momentum, referring to the momentums of multiple objects, or that of a system of objects.
# NEW VERSION(S) OF THE 2ND LAW OF MOTION:
ΣF = (∆p / ∆t) (Average)
ΣF = (dp / dt) (Instantaneous)
This equation is derived from the original 2nd law and from the momentum equation. It is fairly obvious to derive, and as such the proof will not be reproduced here.
The original version of the 2nd law of motion, with its m × a and whatnot, assumes that mass is constant. However, in our modern day and age, we cannot settle for this. These equations enable mass to change - rockets, for example, will lose mass as they expel fuel, and the momentum version of the 2nd law will remain perfectly usable as it does so.
#
P. Rule .
Conservation of Momentum:
A system is "isolated" when the net force on the system is zero. Momentum is conserved in all isolated systems:
Σpi = Σpf
As you can see, this equation accounts for changes in the mass of a system, so long as there is a proportional change in the velocity that will result in momentum being conserved. The initial point is assumed to be right before the collision or explosion, and the final point is assumed to be right after.
Momentum is conserved during all collisions and explosions. In Physics terms, an explosion is essentially just a collision in reverse.
REMEMBER: Conservation of momentum can be done in individual directions or combined - finding values using a conservation equation isolated to a particular direction can be very useful and necessary at times.
For example: when you stand on a skateboard and you are holding a ball, the system consists of you, the skateboard, and the ball. You start off with an initial momentum of zero, because you are not moving. When you throw that ball in one direction, the ball obtains a velocity, which means it patently does not have a momentum of zero. In order for the net momentum of the system to be zero (since one part of the system is moving), the other part of the system must move in the opposite direction (with the same force, of course) so that the total momentum of the system will cancel out and remain zero. This follows both the 3rd law of motion and ensures the conservation of momentum.
A system is "isolated" when the net force on the system is zero. Momentum is conserved in all isolated systems:
Σpi = Σpf
As you can see, this equation accounts for changes in the mass of a system, so long as there is a proportional change in the velocity that will result in momentum being conserved. The initial point is assumed to be right before the collision or explosion, and the final point is assumed to be right after.
Momentum is conserved during all collisions and explosions. In Physics terms, an explosion is essentially just a collision in reverse.
REMEMBER: Conservation of momentum can be done in individual directions or combined - finding values using a conservation equation isolated to a particular direction can be very useful and necessary at times.
For example: when you stand on a skateboard and you are holding a ball, the system consists of you, the skateboard, and the ball. You start off with an initial momentum of zero, because you are not moving. When you throw that ball in one direction, the ball obtains a velocity, which means it patently does not have a momentum of zero. In order for the net momentum of the system to be zero (since one part of the system is moving), the other part of the system must move in the opposite direction (with the same force, of course) so that the total momentum of the system will cancel out and remain zero. This follows both the 3rd law of motion and ensures the conservation of momentum.
#
P. Rule .
TYPES OF COLLISIONS:
Momentum is conserved in all of these, because they are all collisions (as explained in Rule 118).
Momentum is conserved in all of these, because they are all collisions (as explained in Rule 118).
- Elastic Collision: A collision in which the total kinetic energy of a system of the two colliding bodies is unchanged by the collision, conserving the kinetic energy of the system. Generally, the objects "bounce" off of one another in these types of collisions. Even if a question says that air resistance and friction are negligible, that does not mean that the collision is elastic. The only true way to ensure the elasticity of a collision (if it is not stated in the problem) is to calculate the kinetic energy before and after the collision and check if they are equal.
- Inelastic Collision: A collision in which kinetic energy is NOT conserved. In these collisions, some energy is converted from kinetic energy to other forms of energy, like thermal, light, or sound energy (think friction). Inelastic collisions cause objects to deform, causing the kinetic energy to turn into thermal energy.
- Perfectly/Completely Inelastic Collision: Another collision in which kinetic energy is NOT conserved. In these collisions, the objects stick to one another upon colliding. This is scenario with the greatest possible loss of kinetic energy. However, this does not necessarily mean that the objects will stop moving - if you throw a ball into a box on a skateboard, that will be a perfectly inelastic collision even though the skateboard and the entire system will begin moving (due to the conservation of momentum, assuming that the ball is apart of the system).
# Impulse: VECTOR.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation(s): J = ∆p
$$\vec{J} = \int_{t_i}^{t_f} \sum \vec{F} \, dt$$ J = Favg × ∆t (used for approximations)
J = Impulse.
p = Momentum.
F = Force.
ti = Time Initial.
tf = Time Final.
Favg = Average Force.
∆t = Change in Time.
Definition: Just another way of referring to the change in momentum, in a cooler way. The second equation was derived from the instantaneous definition of the new version of the 2nd law of motion.
#
P. Rule .
Impulse Approximation:
During collisions with short time intervals, the force of impact is much larger than all the other forces. Therefore, all other forces can be considered to be negligible when compared to the impact force and the net force is approximately equal to the force of impact.
tl;dr: With collisions that have short ∆t, ΣF ≈ Fimpact
The shorter the time length, the more accurate this approximation gets. The third equation listed in the Impulse definition is best fit for approximations.
During collisions with short time intervals, the force of impact is much larger than all the other forces. Therefore, all other forces can be considered to be negligible when compared to the impact force and the net force is approximately equal to the force of impact.
tl;dr: With collisions that have short ∆t, ΣF ≈ Fimpact
The shorter the time length, the more accurate this approximation gets. The third equation listed in the Impulse definition is best fit for approximations.
#
P. Rule .
With respect to impulse, consider time and force to be inversely proportional to eachother. Because the impulse of a collision will be constant, if there is a shorter time length of the collision, the Force will be higher, and if the collision occurs over a longer period of time, then the force will be smaller, since either way they need to equal the same constant (impulse) when multiplied.
# THE LAST WORD:
The Equation of Conservation of Energy requires a minimum of two objects. Of course, this does not mean that these objects must remain constant throughout the problem - you could possibly have a single object in the beginning that could explode into three objects, resulting in one object on the left side of the equation and three on the right side. Or, possibly, you could have a Perfect Inelastic Collision occur, resulting in two objects on the left side and one object on the right.
The Force of Impact equation (the alt. 2nd law of motion equation) and the Impulse equations each only allow for one object.
It is easy to forget the point of Physics is to have FUN! Playing around with the variables is a great way to relieve stress.
IX. Rotational Dynamics
IX.I Moment of Inertia.
Translational Motion = The movement through space of the center of mass of the object.
Rotational Motion = The movement of an object through circular motion about its center of mass.
A BICYCLE will be in both Translational and Rotational motion when it is in use.
# Moment of Inertia: SCALAR.
Units: Joules (Newton Meters).
Equation:
(for systems of particles) $$I = \sum_{n=1} m_n\,\, r_n^2$$ (for rigid objects with constant density) $$I = \int r^2 \, dm$$
I = Moment of Inertia.
m = The mass of each particle.
r = The distance each particle is from the axis of rotation (the center of the rotation).
dm = Each infinitesimally small particle composing the object.
Definition: Also known as Rotational Mass or Rotational Inertia. A measure of resistance to Angular Acceleration, as opposed to Inertial mass, which is a measure of an object's resistance to acceleration in general. For the full derivation of the formula (and how it connects into Rotational Kinetic Energy), see Rule 122.
The moment of inertia of an entire system is just the summation of all of the individual moments of inertias of the objects within the system. To sum rotational inertias, literally just add them all together, even if they are of different types: if a system contains a particle and a thin rod, then add the particle rotational inertia equation to the thin rod rotational inertia, which has an already known alternate equation (see "Basic Rotational Inertias"). Note: This is only so long as the inertias are calculated around the same axis of rotation.
If you ever need to find the rotational inertia of a non-particle that doesn't have a generalized inertia already known, then you need to use either the rotational kinetic energy equation (if you know the value (see Rule 122)), or the net torque equation (which is equal to I × α, see Rule 125).
In essence, the equations for moment of inertia state that as the distance from the axis of rotation increases, so will the moment of inertia. For example - if you have a broom and you try to rotate it from the brush, it will not be too difficult since most of the mass is located by the brush, but if you were to try to rotate the broom from the top of the handle, it will be much more difficult as the bulk of the mass has dramatically increased in its distance from the center of the rotation.
#
P. Rule .
Kinetic Energy of Rotation:
The Kinetic Energy of old has failed us. Since the classic kinetic energy formula is only with regard to the center of mass of the object (this is called "translational" kinetic energy), a uniform object in rotational motion would be considered to have zero kinetic energy - ignorantly. This equation is inadequate to deal with such pressing questions of modern Physics as the kinetic energy contained in a spinning object - all objects in motion must have kinetic energy.
Thus, a new form of kinetic energy must be discovered: the summation of the kinetic energies of every particle of the system, in the process reimagining the object as a system of particles, each with its own velocity that can contribute to the whole: $$\sum_{n=1} \frac{1}{2} m_n \left(v_n\right)^2$$ Since the velocity in this equation is the tangential velocity, the formula of tangential velocity can be substituted in, producing the following: $$\sum_{n=1} \frac{1}{2} m_n\,\, r_n^2\,\,\, ω^2$$ In all rigid objects with a constant shape, the angular velocity of each particle is the same, and so there is no need for the n subscript to be applied to the ω. Thus, when removing all constants from the equation, you are left with what is known as the Moment of Inertia, represented as the letter I: $$I = \sum_{n=1} m_n\,\, r_n^2$$ Now, the Rotational Kinetic Energy equation has been created: (1/2) × I × ω². The old Translational Kinetic Energy equation ((1/2) × m × v²) was only concerned with the motion of the center of mass of the object, and now, we can use the rotational KE to determine the energy of objects that are merely spinning.
During all conservation of mechanical energy problems, you must account for both Translational and Rotational Kinetic Energy. An object can be in rotational and translational motion at the same time, occurring when both the center of mass of the object is moving through space, and the object itself is in centripetal motion, such as when the object is rolling.
The Kinetic Energy of old has failed us. Since the classic kinetic energy formula is only with regard to the center of mass of the object (this is called "translational" kinetic energy), a uniform object in rotational motion would be considered to have zero kinetic energy - ignorantly. This equation is inadequate to deal with such pressing questions of modern Physics as the kinetic energy contained in a spinning object - all objects in motion must have kinetic energy.
Thus, a new form of kinetic energy must be discovered: the summation of the kinetic energies of every particle of the system, in the process reimagining the object as a system of particles, each with its own velocity that can contribute to the whole: $$\sum_{n=1} \frac{1}{2} m_n \left(v_n\right)^2$$ Since the velocity in this equation is the tangential velocity, the formula of tangential velocity can be substituted in, producing the following: $$\sum_{n=1} \frac{1}{2} m_n\,\, r_n^2\,\,\, ω^2$$ In all rigid objects with a constant shape, the angular velocity of each particle is the same, and so there is no need for the n subscript to be applied to the ω. Thus, when removing all constants from the equation, you are left with what is known as the Moment of Inertia, represented as the letter I: $$I = \sum_{n=1} m_n\,\, r_n^2$$ Now, the Rotational Kinetic Energy equation has been created: (1/2) × I × ω². The old Translational Kinetic Energy equation ((1/2) × m × v²) was only concerned with the motion of the center of mass of the object, and now, we can use the rotational KE to determine the energy of objects that are merely spinning.
During all conservation of mechanical energy problems, you must account for both Translational and Rotational Kinetic Energy. An object can be in rotational and translational motion at the same time, occurring when both the center of mass of the object is moving through space, and the object itself is in centripetal motion, such as when the object is rolling.
# Basic Rotational Inertias:
Here are the Moments of Inertia of some basic rigid objects with constant density. Recall that 'M' is mtotal.
Type, Axis of Rotation
Thin rod of length L, about its center of mass: I = (1/12) × M × L²
Thin rod of length L, about one end: I = (1/3) × M × L²
Thin hollow cylinder (hoop), about its long cylindrical axis: I = MR²
Solid cylinder/disk, about its long cylindrical axis: I = (1/2) × M × R²
Solid sphere, about its center of mass: I = (2/5) × M × R²
Thin hollow sphere/shell, about its center of mass: I = (2/3) × M × R²
Solid slab/block, about its center of mass (perp.): I = (1/12) × M × (a² + b²)
Note that in all where length is irrelevant to the moment of inertia, such as with the cylinders, an object of that type of any length will have the same moment of inertia, from a ring to a mile-long tube.
Derivations: [1] [2] [3]
IX.II Torque.
Units: Newton Meters (Joules). When in reference to Torque, the explicit units "Newton Meters" are used instead of "Joules" to differentiate it from the Scalar units of Work and Kinetic Energy.
Equation:
τ = r × F × sinθ
τ = Torque.
F = The magnitude of the force causing the torque.
r = The magnitude of the position vector from the axis of rotation to the point the force is applied to the object, the magnitude being the base distance. Thus, the farther the distance from the AOR that the force is applied, the greater the r.
θ = The angle between the direction of r and the direction of F.
Definition: The ability of a force to cause an angular acceleration in an object. Just as translational motion is caused by a net force (the ability to cause an acceleration in an object), rotational motion is caused by a net torque. Of course, torque is caused by a force.
The direction of torque, being a result of the cross product, requires only the traditional right-hand rule for determination, back in Subsection III.II. Note that torque is in the same direction as the angular acceleration that it produces, which is also the same direction as the angular velocity or angular displacement, determined through the Rotational RHR (see Rule 51). Choose which one you use based on the parameters of the problem/situation. Either rule patently does not give you the direction of force - figure that out using vector decomposition or something else.
#
P. Rule .
ANALYSIS OF TORQUE.
Think of the opening of a door: The door handle will be positioned as far from the hinges as possible, since the hinges represent the axis of rotation. If you push on the part of the door close to the hinges, it will barely budge. This is because by pushing farther away from the hinges, a larger r value is created (thus producing more torque), and by pushing close the hinges, a smaller r value is created, thus creating less torque.
Furthermore, the angle at which the door is pushed will matter significantly due to the sin curve - the maximum value for the sine of angle is at 90 degrees (1), so pushing perpendicular to the door will result in the most angular acceleration, while other degrees will produce less. A perpendicular force would produce the minimum force necessary to produce torque - other angles at which force can be applied would require higher magnitudes of force to reach the same level of torque. If you push directly parallelly to the direction of r, e.g. directly toward the hinges from the side of the handle, then an angle of 180 will be created, resulting in no torque whatsoever (since sin(180) = 0).
UNDERSTANDING OF THE UTMOST IMPORTANCE:
θ represents the angle between the DIRECTIONS of r and F. You must always be careful to determine the directions of r and F before you make any judgements as to θ.
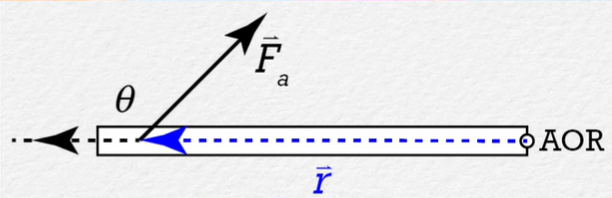
Understand that the direction of the r vector is whichever one in which the distance from the axis of rotation is increasing. Thus, for a door, the direction will be toward the knob and away from the hinges. An example of these concepts can be seen in the figure below, which depicts a door with an unusual force being applied and the resultant θ:
A diagram of a door (the hinges/axis of rotation labeled as AOR) having a non-perpendicular force applied to it. This produces a θ to the left of the force. This highlights a difference between torque and work. Courtesy of Flipping Physics.
Torque is NOT the same as work - torque uses the direction of the variables.
Think of the opening of a door: The door handle will be positioned as far from the hinges as possible, since the hinges represent the axis of rotation. If you push on the part of the door close to the hinges, it will barely budge. This is because by pushing farther away from the hinges, a larger r value is created (thus producing more torque), and by pushing close the hinges, a smaller r value is created, thus creating less torque.
Furthermore, the angle at which the door is pushed will matter significantly due to the sin curve - the maximum value for the sine of angle is at 90 degrees (1), so pushing perpendicular to the door will result in the most angular acceleration, while other degrees will produce less. A perpendicular force would produce the minimum force necessary to produce torque - other angles at which force can be applied would require higher magnitudes of force to reach the same level of torque. If you push directly parallelly to the direction of r, e.g. directly toward the hinges from the side of the handle, then an angle of 180 will be created, resulting in no torque whatsoever (since sin(180) = 0).
UNDERSTANDING OF THE UTMOST IMPORTANCE:
θ represents the angle between the DIRECTIONS of r and F. You must always be careful to determine the directions of r and F before you make any judgements as to θ.
Understand that the direction of the r vector is whichever one in which the distance from the axis of rotation is increasing. Thus, for a door, the direction will be toward the knob and away from the hinges. An example of these concepts can be seen in the figure below, which depicts a door with an unusual force being applied and the resultant θ:
A diagram of a door (the hinges/axis of rotation labeled as AOR) having a non-perpendicular force applied to it. This produces a θ to the left of the force. This highlights a difference between torque and work. Courtesy of Flipping Physics.
Torque is NOT the same as work - torque uses the direction of the variables.
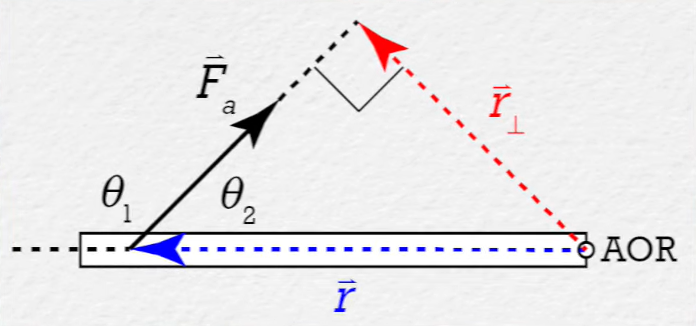
# Moment Arm/Lever Arm: The Perpendicular distance between the line of action of the force and the axis of rotation. The "line of action" is just the artificial extension of the force through space until it can form a right angle with the also artificially created "moment arm". Imagine that r and F are two sides of a right triangle. The third side, which will never be the hypotenuse, is a component of the r position vector. The third side will thus be perpendicular to the force, and, as the perpendicular component of r, is known as the "moment arm" or the "lever arm".
When θ is 90 degrees (a perpendicular force), then r and the moment arm are equal in magnitude, and the Force is the hypotenuse.
Through the forces of trigonometry, the moment arm is equal to r × sinθ, since the sine of any supplementary angles (θ1 and θ2 in the figure) will produce the same value, as one can demonstrate using the sine curve.
This is something that you are guaranteed to do during a problem at some point: use the moment arm to simplify an equation involving a moving particle into just constants. The angular momentum for a moving particle equation, r × m × v × sinθ (see Rule 136), can be simplified very quickly into y × m × v, y being the moment arm perpendicular to the distance between the particle and the center of mass, and to the force. This can be done through pure trigonometry, since y = r × sinθ.
An example of how the moment arm can be constructed using the line of action of the force, and the position vector. Courtesy of Flipping Physics.
#
P. Rule .
Torque Summations:
To sum the torques of the various forces acting upon a position vector, you merely have to add all of the calculated torques of each force together (calculated using the torque equation seen in the torque definition). Make sure to determine the direction of each torque using the right-hand rule, as this will tell you which torques are negative or positive. The sign of your answer will serve as the "direction" of the torque, either positively or negatively perpendicular to the force and position vector.
When summing the torques, you have to sum the torque of EVERY force, including gravity and the normal force. If the axis of rotation is centered at the center of mass, then the torque of gravity can be set to zero since it has an r of 0. You must be careful not to place the normal force as being located at the center of mass of the object - that is an old oversight that must be corrected - See Rule 139.
Note that the summed torques is one half of an equality described in the rotational form of Newton's Second Law (Rule 125), which is the rotational equivalent to ΣF = ma. If a question is only asking to find "the net torque", just sum the torques without setting it equal to I × α.
To sum the torques of the various forces acting upon a position vector, you merely have to add all of the calculated torques of each force together (calculated using the torque equation seen in the torque definition). Make sure to determine the direction of each torque using the right-hand rule, as this will tell you which torques are negative or positive. The sign of your answer will serve as the "direction" of the torque, either positively or negatively perpendicular to the force and position vector.
When summing the torques, you have to sum the torque of EVERY force, including gravity and the normal force. If the axis of rotation is centered at the center of mass, then the torque of gravity can be set to zero since it has an r of 0. You must be careful not to place the normal force as being located at the center of mass of the object - that is an old oversight that must be corrected - See Rule 139.
Note that the summed torques is one half of an equality described in the rotational form of Newton's Second Law (Rule 125), which is the rotational equivalent to ΣF = ma. If a question is only asking to find "the net torque", just sum the torques without setting it equal to I × α.
#
P. Rule .
Rotational Form of Newton's Second Law:
Στ = I × α.
The sum of the torque (that of the various forces acting upon an object) is equal to the moment of inertia times the angular acceleration. The angular acceleration is directly proportional to the magnitude of the net torque, and is inversely proportional to the moment of inertia.
In order to use this equation, you must identify the objects with torque, the axis of rotation of them, and which direction is positive torque.
Στ = I × α.
The sum of the torque (that of the various forces acting upon an object) is equal to the moment of inertia times the angular acceleration. The angular acceleration is directly proportional to the magnitude of the net torque, and is inversely proportional to the moment of inertia.
In order to use this equation, you must identify the objects with torque, the axis of rotation of them, and which direction is positive torque.
# Rotational Equilibrium: When, as a result of a net zero torque (which in turn causes zero angular acceleration), the object remains at rest or at a constant angular velocity.
This is just like Translational Equilibrium, which is when a net force of zero on an object (and thus zero acceleration) results in the object being either at rest or at a constant velocity.
Note that it is impossible for the rotational inertia to be equal to zero so long as there is any mass located away from the axis of rotation, which is in all real circumstances.
# Static Equilibrium: A state in which an object is at rest and not rotating. Thus, the object is in both Translational and Rotational Equilibrium at the same time. Additionally, the net torque of any axis of rotation will equal zero.
The ability to use both torque and regular force equations can be super useful, especially with the ability to place the axis of rotation on any spot (and thus nullifying any forces acting on that spot in the torque equations, since the r for that force would be zero).
#
P. Rule .
In all situations, if there are objects that are on top of other objects, and you are including the bottom objects in your force summation, then you do not need to include the force normals of the objects on top, only their forces of gravity. This is because the weight of the top objects will just contribute to the force normal of the bottom object.
Secondly, ALWAYS include ALL of the objects in the summation of the torques, including the objects on bottom and on top and anything in between. When determining if the torques are positive or not, don't forget you need to use the old right hand rule to figure it out, using the forces as your guide. Draw out the free-body diagram and draw the arrows on the forces to make it easier on yourself.
Don't forget the principle of single direction (see Rule 76) in all pulley problems. The direction you decide the torque to be moving in will change how you conduct force summations for any hanging objects, summing with regard to the direction that you decided would be positive, whether it be the clockwise or counter-clockwise movement of the pulley. Thus, for an object on the side of the pulley that would denote positive movement (whatever you decided that means) would have the force of gravity as a negative force, while a hanging object on the other side would have gravity as a positive.
Secondly, ALWAYS include ALL of the objects in the summation of the torques, including the objects on bottom and on top and anything in between. When determining if the torques are positive or not, don't forget you need to use the old right hand rule to figure it out, using the forces as your guide. Draw out the free-body diagram and draw the arrows on the forces to make it easier on yourself.
Don't forget the principle of single direction (see Rule 76) in all pulley problems. The direction you decide the torque to be moving in will change how you conduct force summations for any hanging objects, summing with regard to the direction that you decided would be positive, whether it be the clockwise or counter-clockwise movement of the pulley. Thus, for an object on the side of the pulley that would denote positive movement (whatever you decided that means) would have the force of gravity as a negative force, while a hanging object on the other side would have gravity as a positive.
#
P. Rule .
To solve static equilibrium problems, you can chose 1 of two placements of the axis of rotation for your torque summations:
1. You can set the axis of rotation all the way to the end of the main object (the saw or meterstick or whichever similar object), which can best be done in circumstances where the force normal has already been determined (whether through the y-direction force summation or other means).
2. You can set the axis of rotation to be at an exact point, whether one you want to find (such as a point whose r value you are trying to find) or one you want to remove all together in order to isolate another variable (in situations which you have two unknown variables, and placing the axis of rotation upon one point will remove that variable, allowing the other one to be solved).
1. You can set the axis of rotation all the way to the end of the main object (the saw or meterstick or whichever similar object), which can best be done in circumstances where the force normal has already been determined (whether through the y-direction force summation or other means).
2. You can set the axis of rotation to be at an exact point, whether one you want to find (such as a point whose r value you are trying to find) or one you want to remove all together in order to isolate another variable (in situations which you have two unknown variables, and placing the axis of rotation upon one point will remove that variable, allowing the other one to be solved).
#
P. Rule .
There is a trend in Physics and Mathematics equations that you will see rather commonly: Lowercase letters are in reference to variables, like the 'r' and 'dm' of the integral equation of moment of inertia equations. Uppercase letters, on the other hand, are in reference to constants, such as the 'R', 'M', and 'L''s of the basic rotational inertias.
#
P. Rule .
Parallel Axis Theorem:
Iparallel = ICOM + M × D²
Iparallel = The moment of inertia parallel to an axis through center of mass.
ICOM = The moment of inertia going directly through an axis through center of mass.
M = The total mass of the rigid body.
D = The distance from the center of mass to the new axis. This is NOT the distance from the old axis of rotation to the new one, it is the distance from the center of mass.
This theorem is an easy way to determine the moment of inertia of a rigid body, rotating about an axis parallel to the true axis that runs through the center of mass of the rigid body. This theorem greatly simplifies the process of determining moment of inertia for various objects (given you already know the parent one), such as in determining the moment of inertia of a thin rod of length L about one of its ends, given you already know the moment of inertia of the rod rotating around its center of mass (e.g., you can determine the second value of "Basic Rotational Inertias" from the first).
Iparallel = ICOM + M × D²
Iparallel = The moment of inertia parallel to an axis through center of mass.
ICOM = The moment of inertia going directly through an axis through center of mass.
M = The total mass of the rigid body.
D = The distance from the center of mass to the new axis. This is NOT the distance from the old axis of rotation to the new one, it is the distance from the center of mass.
This theorem is an easy way to determine the moment of inertia of a rigid body, rotating about an axis parallel to the true axis that runs through the center of mass of the rigid body. This theorem greatly simplifies the process of determining moment of inertia for various objects (given you already know the parent one), such as in determining the moment of inertia of a thin rod of length L about one of its ends, given you already know the moment of inertia of the rod rotating around its center of mass (e.g., you can determine the second value of "Basic Rotational Inertias" from the first).
#
P. Rule .
Do not forget how to correlate rotational and linear acceleration/velocity - you learned this before.
On a pulley system in which a string pull downward upon the circular pulley, pulling into centripetal motion, the pulley will be accelerating (angularly) at a proportional rate to the string (linearly), since the string can only move downward as the pulley/circular object moves with it. In these circumstances, remember that the string is moving at a tangential acceleration, which already has a proportionality defined for it:
at = r × α.
Tangential Velocity is practically the same thing as well, just with angular velocity instead of acceleration.
Do not forget the basic equations of centripetal motion when doing problems involving torque and moment of inertia! Reflect and review the old equations here.
On a pulley system in which a string pull downward upon the circular pulley, pulling into centripetal motion, the pulley will be accelerating (angularly) at a proportional rate to the string (linearly), since the string can only move downward as the pulley/circular object moves with it. In these circumstances, remember that the string is moving at a tangential acceleration, which already has a proportionality defined for it:
at = r × α.
Tangential Velocity is practically the same thing as well, just with angular velocity instead of acceleration.
Do not forget the basic equations of centripetal motion when doing problems involving torque and moment of inertia! Reflect and review the old equations here.
#
P. Rule .
Negligible friction: Though a pulley can be stated to have "negligible friction", if this were actually true, any strings/wire upon it would just slide off and the pulley would never rotate. The meaning of "negligible friction" when stated with regard to a pulley is that the Axle of the pulley, the center rotatinal axis, has negligible friction - the surface of the pulley still has the necessary friction to interact with the string, enough so that the acceleration of the pulley and the string are proportional to one another. See Rule 130 for an explanation.
# Cycloid: A curve traced by a point on a circle rolling in a straight line.
Cycloid. Courtesy of Wikimedia.
#
P. Rule .
All objects that roll without slipping, such as cylinders and all good tires, have a total kinetic energy that equals the sum of the translational and rotational kinetic energies of the object:
KEtotal = KET + KER
KEtotal = (½ × m × v²) + (½ × I × ω²)
The acceleration of all objects that roll without slipping only relies on three determinants: the force of gravity, the incline angle, and the coefficient of the moment of inertia. The lower the fraction for the rotational inertia equation (where both gravity and the incline are constant), the lower the percentage of the initial gravitational potential energy that will be converted into rotational kinetic energy as the object rolls without sliding. Thus, more of the potential energy will be converted directly into translational kinetic energy, and thus the object will have a higher final velocity, thus moving down the incline faster.
For example, if a hollow sphere and a solid sphere (the radius of each being negligible) were both to begin rolling down an incline at the same time, the solid sphere would reach the bottom first since it has a smaller moment of inertia than the hollow sphere: 2/5 < 2/3.
If you do not know either component variable of rotational inertia (either mass & length or mass & radius), then it can be better not to substitute in the equation for rotational inertia into the problem, to leave I as only one unknown in the rotational kinetic energy equation. Sometimes, problems will tell you the specificities for a known moment of inertia ("a thin rod that rotates around one end"), but they will only serve as red herrings when no information as to the components of inertial mass is given, and so isolating the variable I itself and solving it outright will be the correct solution.
Do not fall into the dogma of having to substitute every possible equation in at all times - solving something on a higher level first can help you in many different ways.
KEtotal = KET + KER
KEtotal = (½ × m × v²) + (½ × I × ω²)
The acceleration of all objects that roll without slipping only relies on three determinants: the force of gravity, the incline angle, and the coefficient of the moment of inertia. The lower the fraction for the rotational inertia equation (where both gravity and the incline are constant), the lower the percentage of the initial gravitational potential energy that will be converted into rotational kinetic energy as the object rolls without sliding. Thus, more of the potential energy will be converted directly into translational kinetic energy, and thus the object will have a higher final velocity, thus moving down the incline faster.
For example, if a hollow sphere and a solid sphere (the radius of each being negligible) were both to begin rolling down an incline at the same time, the solid sphere would reach the bottom first since it has a smaller moment of inertia than the hollow sphere: 2/5 < 2/3.
If you do not know either component variable of rotational inertia (either mass & length or mass & radius), then it can be better not to substitute in the equation for rotational inertia into the problem, to leave I as only one unknown in the rotational kinetic energy equation. Sometimes, problems will tell you the specificities for a known moment of inertia ("a thin rod that rotates around one end"), but they will only serve as red herrings when no information as to the components of inertial mass is given, and so isolating the variable I itself and solving it outright will be the correct solution.
Do not fall into the dogma of having to substitute every possible equation in at all times - solving something on a higher level first can help you in many different ways.
#
P. Rule .
The acceleration and velocities of the center of masses of objects that roll without slipping (translational, obviously) also have their own equations, totally identical to their tangential equivalents:
vcom = R × ω
acom = R × α
Thus, very importantly, in these circumstances, the angular and linear accelerations/velocities will be in the same direction. If you are not getting that when you solve the problem, change the positive direction of the torque.
The equation for the distance travelled by the center of mass of the rolling object is similar to the arc length equation:
∆xcom = R × ∆θ
vcom = R × ω
acom = R × α
Thus, very importantly, in these circumstances, the angular and linear accelerations/velocities will be in the same direction. If you are not getting that when you solve the problem, change the positive direction of the torque.
The equation for the distance travelled by the center of mass of the rolling object is similar to the arc length equation:
∆xcom = R × ∆θ
IX.III Angular Momentum.
#
P. Rule .
Angular Momentum: VECTOR.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: (For Rigid Objects with Shape)
L = I × ω
L = Angular Momentum, represented with an 'L' instead of rho.
I = Moment of Inertia.
ω = Angular Velocity.
Definition: "Rotational Inertia in Motion", the property of an object in centripetal motion to remain in the state of centripetal motion.
Notice that since angular momentum and angular velocity are directly proportional vectors, they must be in the same direction. Determine direction using the rotational right hand rule. Furthermore, L has an inherent axis of rotation that must be identified every time, like torque and rotational inertia. Watch this for the derivation of the equation.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: (For Rigid Objects with Shape)
L = I × ω
L = Angular Momentum, represented with an 'L' instead of rho.
I = Moment of Inertia.
ω = Angular Velocity.
Definition: "Rotational Inertia in Motion", the property of an object in centripetal motion to remain in the state of centripetal motion.
Notice that since angular momentum and angular velocity are directly proportional vectors, they must be in the same direction. Determine direction using the rotational right hand rule. Furthermore, L has an inherent axis of rotation that must be identified every time, like torque and rotational inertia. Watch this for the derivation of the equation.
#
P. Rule .
Conservation of Angular Momentum:
ΣLi = ΣLf
Expanded, this is the following:
Ii × ωi = If × ωf
Add as many additional angular momentums into the equation as there are objects in the system.
The conservation of angular momentum equation can be easily derived from a special case of the net external torque equation:
Στexternal = (∆Lsystem / ∆t)
Thus, if the object is not in centripetal motion at the beginning of the event (initial torque = 0), then if angular momentum is conserved, it will continue to have 0 centripetal motion at the end. If an external force causes centripetal motion to be created, then angular momentum is not conserved. See Rule 100 & Rule 101 to determine what forces are external or not.
General Example: When a figure skater pulls their arms inward during a performance, they will speed up. This is because they are reducing the distance of some amount of mass from their center of mass, thus decreasing the moment of inertia and causing the angular velocity to increase so that angular momentum is conserved.
ΣLi = ΣLf
Expanded, this is the following:
Ii × ωi = If × ωf
Add as many additional angular momentums into the equation as there are objects in the system.
The conservation of angular momentum equation can be easily derived from a special case of the net external torque equation:
Στexternal = (∆Lsystem / ∆t)
Thus, if the object is not in centripetal motion at the beginning of the event (initial torque = 0), then if angular momentum is conserved, it will continue to have 0 centripetal motion at the end. If an external force causes centripetal motion to be created, then angular momentum is not conserved. See Rule 100 & Rule 101 to determine what forces are external or not.
General Example: When a figure skater pulls their arms inward during a performance, they will speed up. This is because they are reducing the distance of some amount of mass from their center of mass, thus decreasing the moment of inertia and causing the angular velocity to increase so that angular momentum is conserved.
#
P. Rule .
In the SPECIFIC CASE of a point particle moving in a circle (centripetal motion), the following attributes are applicable to the particle:
1. Translational and Rotational Kinetic Energy will return the same value (only in these circumstances!). Choose either depending on what variables you have.
2. The angular momentum of the particle can be calculated using both the 'rigid object with shape' momentum equation (I × ω) and the translational point-particle momentum equation: Lparticle = r × m × v × sinθ.
r - The vector from axis of rotation to center of mass of particle.
m - The mass of the point particle.
v - The linear velocity of the point particle.
θ - The angle between the DIRECTIONS r and v, like torque.
This equation can additionally be used for all translationally moving point particles (which, indeed, have angular momentum insofar as how it could translate to another object obtaining that angular momentum following a collision).
Attribute #1 is also applicable for ellipses, though not #2.
1. Translational and Rotational Kinetic Energy will return the same value (only in these circumstances!). Choose either depending on what variables you have.
2. The angular momentum of the particle can be calculated using both the 'rigid object with shape' momentum equation (I × ω) and the translational point-particle momentum equation: Lparticle = r × m × v × sinθ.
r - The vector from axis of rotation to center of mass of particle.
m - The mass of the point particle.
v - The linear velocity of the point particle.
θ - The angle between the DIRECTIONS r and v, like torque.
This equation can additionally be used for all translationally moving point particles (which, indeed, have angular momentum insofar as how it could translate to another object obtaining that angular momentum following a collision).
Attribute #1 is also applicable for ellipses, though not #2.
#
P. Rule .
When a questions asks just for the "acceleration", "velocity", or "speed" of an object or a system, it is general principle to find the linear quanity, unless the question specifically asks for the angular version.
#
P. Rule .
Pulleys with Mass:
Pulleys with mass have rotational inertia. Pulleys without mass do not have rotational inertia.
Where as before, the force of tension (magnitude) applied on each side of the pully was the same, this is not the case in pulleys with mass: These pulleys will have rotational inertia due to their mass, and thus will resist angular acceleration, making the two forces of tension acting on either side of the pulley not necesarilly having the same magnitude.
In all problems where the pulley has mass, just incorporate it as another one of the objects you are findings the torques/angular momentum of, and summing the force normal & gravity of the pulley.
Pulleys with mass have rotational inertia. Pulleys without mass do not have rotational inertia.
Where as before, the force of tension (magnitude) applied on each side of the pully was the same, this is not the case in pulleys with mass: These pulleys will have rotational inertia due to their mass, and thus will resist angular acceleration, making the two forces of tension acting on either side of the pulley not necesarilly having the same magnitude.
In all problems where the pulley has mass, just incorporate it as another one of the objects you are findings the torques/angular momentum of, and summing the force normal & gravity of the pulley.
#
P. Rule .
In torque problems, you must always draw the normal force as originating at the point of contact, from the surface the object is resting on.
In the past, the normal force has been drawn as having the center of mass of the object as its origin - this is a simplification, a falsehood that is done purely in problems where such an oversight does not matter.
In problems involving Torque however, the location of the origin of the forces matters significantly, due to how torque is calculated. If the axis of rotation of an object is placed along the center of mass, then all torques acting at the center of mass are equal to 0 since they have a radius of 0 (see Rule 124). By placing the normal force on the center of mass of the object, you would be incorrectly excluding it from all torque summations in all situations where the axis of rotation is upon the center of mass.
In the past, the normal force has been drawn as having the center of mass of the object as its origin - this is a simplification, a falsehood that is done purely in problems where such an oversight does not matter.
In problems involving Torque however, the location of the origin of the forces matters significantly, due to how torque is calculated. If the axis of rotation of an object is placed along the center of mass, then all torques acting at the center of mass are equal to 0 since they have a radius of 0 (see Rule 124). By placing the normal force on the center of mass of the object, you would be incorrectly excluding it from all torque summations in all situations where the axis of rotation is upon the center of mass.
X. Gravitation
X.I Laws of Motion.
#
P. Rule .
Universal Law of Gravitation: VECTOR.
Units: Newtons. It is in the same form as Fg, as will be described.
Equation:
$$F_g = \frac{G \times m_1 \times m_2}{r^2}$$
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
m1 = Mass of the first object.
m2 = Mass of the second object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
Definition: A force of gravitational attraction exists for any two objects, not just an object and the Earth. The equation to determine this force is Newton's Universal Law of Gravitation.
The old force of gravity equation, "Fg = mg" or whatever, is a planet-specific equation, usable only on objects close to a planet and using that planet as one of the masses. Thus, if an object moves from a planet/asteroid a distance that is a significant portion of the planet's radius, then the Universal Law of Gravitation must be used instead of mg. The Law of Gravitation, however, is always correct in all scenarios, including those involving planets.
The given equation provides only the magnitude of the gravitational attraction between two objects, which is always an attractive force that pulls entities together. However, when finding a balance between two objects, like in a problem in which one must calculate an object's placement between two objects of different masses, such that the two pulls in opposite directions result in the object remaining in place (or any problem that requires calculating multiple gravitational pulls), setting a pull in a particular direction to be positive or negative (in relation to another pull) is perfectly fine, and can be necessary for pulls to cancel out (i.e., for them to be equal & opposite).
Units: Newtons. It is in the same form as Fg, as will be described.
Equation:
$$F_g = \frac{G \times m_1 \times m_2}{r^2}$$
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
m1 = Mass of the first object.
m2 = Mass of the second object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
Definition: A force of gravitational attraction exists for any two objects, not just an object and the Earth. The equation to determine this force is Newton's Universal Law of Gravitation.
The old force of gravity equation, "Fg = mg" or whatever, is a planet-specific equation, usable only on objects close to a planet and using that planet as one of the masses. Thus, if an object moves from a planet/asteroid a distance that is a significant portion of the planet's radius, then the Universal Law of Gravitation must be used instead of mg. The Law of Gravitation, however, is always correct in all scenarios, including those involving planets.
The given equation provides only the magnitude of the gravitational attraction between two objects, which is always an attractive force that pulls entities together. However, when finding a balance between two objects, like in a problem in which one must calculate an object's placement between two objects of different masses, such that the two pulls in opposite directions result in the object remaining in place (or any problem that requires calculating multiple gravitational pulls), setting a pull in a particular direction to be positive or negative (in relation to another pull) is perfectly fine, and can be necessary for pulls to cancel out (i.e., for them to be equal & opposite).
# Alternate Definition of Tangential Velocity for Gravitation:
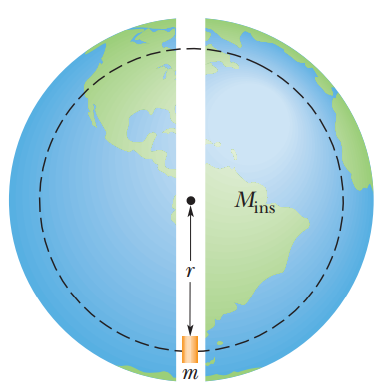
When Gravitation is the only force acting upon an object (such as if the object is in orbit around a planet/asteroid), then an alternate definition of tangential velocity can be created by isolating velocity: $$V_t = \sqrt{\dfrac{G \times m}{r}}$$
# Parallax: When the position of an object appears to differ when viewed from different locations.
# Geocentric Model: The ancient model of the solar system in which a stationary Earth was at the center, with the sun and planets orbiting around it. This model was formalized by Ptolemy in the 1st century A.D. (see A. Rule 18).
# Heliocentric Model: A model of the solar system (widely accepted) in which the Sun is at the center, with the Earth and planets revolving around it. This model was proposed by Copernicus in 1543 (see A. Rule 22), supported by Celestial observations by Tycho Brahe in the late 1500s (see A. Rule 25), and given a mathematical basis by Johannes Kepler in the early 1600s (see A. Rule 26), who had been worked off of the data of Brahe.
#
P. Rule .
Kepler's Three Laws of Planetary Motion were developed over the course of 20 years of hardcore analysis of the data of Tycho Brahe. They are not too complex:
Law of Planetary Motion #1 - Law of Orbits
"Planets move in elliptical orbits with the Sun at one foci/focus point."
The path of an object through space is called its orbit, and has varying degrees of ellipticallity (known as eccentricity). The foci will change their postion depending on the size/nature of the ellipse.
Whereas a circle only has one special point (the center), in an ellipse there are TWO special points, known as the foci, or the focus points of the ellipse. The sum of the distance from the focus points to any position on the ellipse is always the same:
An animated ellipse to illustrate that the sum of the distances from a point to the foci is constant. Courtesy of the UTSA.
As seen above, r1 + r2 = 2a. Always.
The widest diameter of the ellipse is called its Major Axis, while half that distance, the distance from the center of the ellipse from end to end, is called the Semimajor Axis. The smallest diameter of the ellipse is the Minor Axis (of Symmetry), perpendicular to the Major Axis, and it has two semimajor axes at either side of the center as well:
The Major Axis (2a) – the longest diameter of an ellipse, each end point is called a vertex.
The Minor Axis (2b) – the shortest diameter of an ellipse, each end point is called a co-vertex.
The Semimajor Axis (a) – Half of the major axis.
The Semiminor Axis (b) – Half of the minor axis.
Eccentricity (e) – the distance between the two focal points, F1 and F2, divided by the length of the major axis.
(ae) – the distance between one of the focal points and the centre of the ellipse (the length of the Semimajor axis multiplied by the eccentricity). Courtesy of the Science & Math Zone.
The shape/roundness of an ellipse depends on how close together the two foci are, compared with the Major Axis. The ratio of the distance between the foci to the length of the major axis is called the Eccentricity of the ellipse. The equation for eccentricity can be derived as e = (c / a), where a is the length of the semimajor axis and c is the distance between the center of the ellipse to the foci.
If the eccentricity is zero, then the foci will be in the same spot and the ellipse will be a circle. Thus, in elliptical terms, a circle is an ellipse of zero eccentricity with the Semimajor axis as the radius.
The greater the eccentricity, the more elongated the ellipse, up to a maximum eccentricity of 1.0, which is just a flat line. The size and shape of an ellipse are completely specified by its Semimajor axis and its Eccentricity.
Law of Planetary Motion #1 - Law of Orbits
"Planets move in elliptical orbits with the Sun at one foci/focus point."
The path of an object through space is called its orbit, and has varying degrees of ellipticallity (known as eccentricity). The foci will change their postion depending on the size/nature of the ellipse.
Whereas a circle only has one special point (the center), in an ellipse there are TWO special points, known as the foci, or the focus points of the ellipse. The sum of the distance from the focus points to any position on the ellipse is always the same:
An animated ellipse to illustrate that the sum of the distances from a point to the foci is constant. Courtesy of the UTSA.
As seen above, r1 + r2 = 2a. Always.
The widest diameter of the ellipse is called its Major Axis, while half that distance, the distance from the center of the ellipse from end to end, is called the Semimajor Axis. The smallest diameter of the ellipse is the Minor Axis (of Symmetry), perpendicular to the Major Axis, and it has two semimajor axes at either side of the center as well:
The Major Axis (2a) – the longest diameter of an ellipse, each end point is called a vertex.
The Minor Axis (2b) – the shortest diameter of an ellipse, each end point is called a co-vertex.
The Semimajor Axis (a) – Half of the major axis.
The Semiminor Axis (b) – Half of the minor axis.
Eccentricity (e) – the distance between the two focal points, F1 and F2, divided by the length of the major axis.
(ae) – the distance between one of the focal points and the centre of the ellipse (the length of the Semimajor axis multiplied by the eccentricity). Courtesy of the Science & Math Zone.
The shape/roundness of an ellipse depends on how close together the two foci are, compared with the Major Axis. The ratio of the distance between the foci to the length of the major axis is called the Eccentricity of the ellipse. The equation for eccentricity can be derived as e = (c / a), where a is the length of the semimajor axis and c is the distance between the center of the ellipse to the foci.
If the eccentricity is zero, then the foci will be in the same spot and the ellipse will be a circle. Thus, in elliptical terms, a circle is an ellipse of zero eccentricity with the Semimajor axis as the radius.
The greater the eccentricity, the more elongated the ellipse, up to a maximum eccentricity of 1.0, which is just a flat line. The size and shape of an ellipse are completely specified by its Semimajor axis and its Eccentricity.
#
P. Rule .
Law of Planetary Motion #2 - Law of Areas
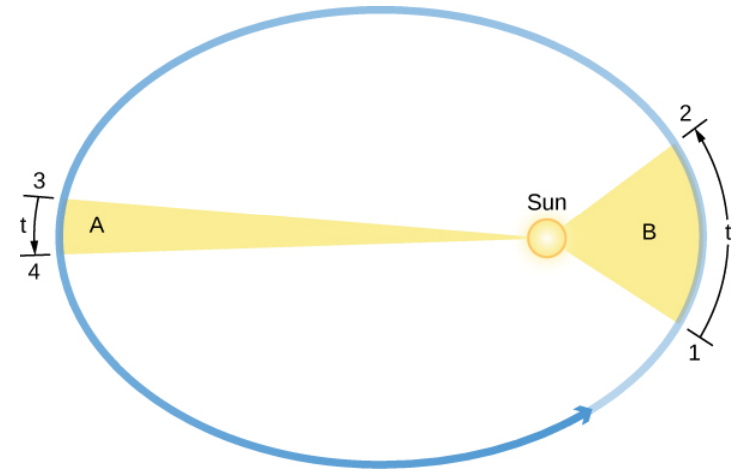
"Each planet moves such that an imaginary line drawn between the sun and the planet sweeps out equal areas in equal time periods."
Kepler determined that Mars moves faster as it comes closer to the Sun, and slows down as it pulls away from the Sun. Therefore, objects in orbit are patently NOT in Uniform Acceleration, unless they have an eccentricity of 0.
Visualize an elastic band connecting a celestial body with the Sun. As the body gets farther from the sun, the band gets stretched, and thus moves slower until the band will pull it back to the sun. When it is closer to the sun, the band is not stretched as much and thus moves rapidly. Additionally, if you were to imagine the area sweeped in the ellipse (centered from the sun) by the orbit, then, given equal intervals of time, any two sweeped areas of the orbit will be equal.
The orbital speed of a planet traveling around the Sun (the circular object inside the ellipse) varies in such a way that in equal intervals of time (t), a line between the Sun and a planet sweeps out equal areas (A and B). Note that the eccentricities of the planets’ orbits in the solar system are substantially less than shown here.
While a circular orbit would cause a planet to move at the same speed throughout its orbit, the differing speeds of the planets as they move make it evident that their orbits are elliptical.
"Each planet moves such that an imaginary line drawn between the sun and the planet sweeps out equal areas in equal time periods."
Kepler determined that Mars moves faster as it comes closer to the Sun, and slows down as it pulls away from the Sun. Therefore, objects in orbit are patently NOT in Uniform Acceleration, unless they have an eccentricity of 0.
Visualize an elastic band connecting a celestial body with the Sun. As the body gets farther from the sun, the band gets stretched, and thus moves slower until the band will pull it back to the sun. When it is closer to the sun, the band is not stretched as much and thus moves rapidly. Additionally, if you were to imagine the area sweeped in the ellipse (centered from the sun) by the orbit, then, given equal intervals of time, any two sweeped areas of the orbit will be equal.
The orbital speed of a planet traveling around the Sun (the circular object inside the ellipse) varies in such a way that in equal intervals of time (t), a line between the Sun and a planet sweeps out equal areas (A and B). Note that the eccentricities of the planets’ orbits in the solar system are substantially less than shown here.
While a circular orbit would cause a planet to move at the same speed throughout its orbit, the differing speeds of the planets as they move make it evident that their orbits are elliptical.
# Astronomical Unit: The average distance between the Sun and the Earth, defined as 149,597,870,700 meters.
#
P. Rule .
Law of Planetary Motion #3 - Law of Periods
"The square of the orbital period of any planet is proportional to the cube of the semimajor axis of the elliptical orbit; in other words, T² ∝ a³."
There are two equations:
The First Equation is best used when comparing two bodies orbiting the same central object, like the Earth and an Asteroid. The ratio can be set up as (TAsteroid / TEarth)² = (rAsteroid / rEarth)³, for example. In such cases, put the new object in the numerator on both sides, as to ease isolation.
The Second Equation is preferable when the orbital period or distance of the reference orbit is unknown, or if the central mass being orbited changes.
E.g., the 1st equation is best suited when the orbited mass already has a reference orbit that can be used (and 3/4th of the variables are known), and the 2nd equation for all other circumstances.
1. T² ∝ a³
2. T² = (4π² / GM) × a³
T - The "Orbital Period", or the time it takes the orbit to record one revolution around the Primary. Measured in Earth-years.
a - The Semimajor Axis (see Rule 141). This is the average distance between the orbiting object and the primary, and is measured in AU.
G - The Universal Gravitational Constant (6.67 x 10⁻¹¹ (N × m²) / (kg²))
M - Mass of the Primary (e.g., the Sun or another star), except in binary systems - in this case, M represents the total mass of the objects.
The equation is derived from the Law of Gravitation and an inward force summation.
"The square of the orbital period of any planet is proportional to the cube of the semimajor axis of the elliptical orbit; in other words, T² ∝ a³."
There are two equations:
The First Equation is best used when comparing two bodies orbiting the same central object, like the Earth and an Asteroid. The ratio can be set up as (TAsteroid / TEarth)² = (rAsteroid / rEarth)³, for example. In such cases, put the new object in the numerator on both sides, as to ease isolation.
The Second Equation is preferable when the orbital period or distance of the reference orbit is unknown, or if the central mass being orbited changes.
E.g., the 1st equation is best suited when the orbited mass already has a reference orbit that can be used (and 3/4th of the variables are known), and the 2nd equation for all other circumstances.
1. T² ∝ a³
2. T² = (4π² / GM) × a³
T - The "Orbital Period", or the time it takes the orbit to record one revolution around the Primary. Measured in Earth-years.
a - The Semimajor Axis (see Rule 141). This is the average distance between the orbiting object and the primary, and is measured in AU.
G - The Universal Gravitational Constant (6.67 x 10⁻¹¹ (N × m²) / (kg²))
M - Mass of the Primary (e.g., the Sun or another star), except in binary systems - in this case, M represents the total mass of the objects.
The equation is derived from the Law of Gravitation and an inward force summation.
# Geosynchronous/Geostationary Orbit: A state of an object orbiting the Earth where it is always positioned directly over the same spot on the Earth. In order for this to be the case, the orbiting body must be directly over the equator.
The orbited body has to be the Earth, for otherwise, it would merely be a Stationary or Synchronous orbit.
# MEarth (Mass of the Earth, Earth Mass): 5.9723 × 10²⁴ kg.
# Equatorial Radius of Earth: 6.378 × 10⁶ m.
#
P. Rule .
Weightlessness:
In order for TRUE weightlessness, the force of gravity acting on an object (the weight) must be equal to zero, and thus the acceleration due to gravity must equal to zero.
Given the Universal Law of Gravitation, the only way to have the force of gravity on an object equal zero is to have infinite amount of distance between the object and everything else in universe, which is impossible. Every particle is exerting is gravitationally attracted to everything else.
Other means of reaching weightlessness while more than one object exists in the universe include placing the object in the center of a uniform spherical shell, in which case the object would be perfectly pulled in every direction to remain stationary. Similarly, the simple case of placing the object between two objects, so that the object will be equally pulled in opposite directions, will leave the object stationary.
Of course, for the "apparent weightlessness" that is simply falling, only the normal force needs to be zero, as is the case with the International Space Station. See Rule 78 for the derivation. Apparent Weightlessness can be simply defined as a state in which zero g-Forces in any direction are acting on an object (zero net g-forces (see Rule 145)).
In order for TRUE weightlessness, the force of gravity acting on an object (the weight) must be equal to zero, and thus the acceleration due to gravity must equal to zero.
Given the Universal Law of Gravitation, the only way to have the force of gravity on an object equal zero is to have infinite amount of distance between the object and everything else in universe, which is impossible. Every particle is exerting is gravitationally attracted to everything else.
Other means of reaching weightlessness while more than one object exists in the universe include placing the object in the center of a uniform spherical shell, in which case the object would be perfectly pulled in every direction to remain stationary. Similarly, the simple case of placing the object between two objects, so that the object will be equally pulled in opposite directions, will leave the object stationary.
Of course, for the "apparent weightlessness" that is simply falling, only the normal force needs to be zero, as is the case with the International Space Station. See Rule 78 for the derivation. Apparent Weightlessness can be simply defined as a state in which zero g-Forces in any direction are acting on an object (zero net g-forces (see Rule 145)).
#
P. Rule .
G-Forces:
The number of "G's" an object has is a ratio of the acceleration experienced by the object with respect to the ordinary acceleration experienced on Earth: If you have a vertical g-force of 2, you are experiencing an apparent weight double to what it normally is.
Since life on Earth dictates there is always a vertical acceleration due to Gravity, a g-force of 1 vertically and 0 horizontally is the "normal", where everything should be as it should. This is the state encountered when at rest.
To have a G-force in the horizontal direction would mean you are doing something very strange, since humans do not usually experience weight horizontally. Generally, the fastest cars only go slightly more than 1 g horizontally at top accelerations. There are two equations that can be used to determine the total number of g-Forces acting on an object:
Vertical # of g-Forces: (FN / FgEarth)
Horizontal # of g-Forces: (ax / gEarth)
FN = The Normal Force an object has, such as that produced by rocket fuel when launching upward.
FgEarth = The gravitational force caused by the Earth.
ax = Acceleration of an object in the x-direction.
gEarth = The acceleration due to gravity of the Earth.
The number of "G's" an object has is a ratio of the acceleration experienced by the object with respect to the ordinary acceleration experienced on Earth: If you have a vertical g-force of 2, you are experiencing an apparent weight double to what it normally is.
Since life on Earth dictates there is always a vertical acceleration due to Gravity, a g-force of 1 vertically and 0 horizontally is the "normal", where everything should be as it should. This is the state encountered when at rest.
To have a G-force in the horizontal direction would mean you are doing something very strange, since humans do not usually experience weight horizontally. Generally, the fastest cars only go slightly more than 1 g horizontally at top accelerations. There are two equations that can be used to determine the total number of g-Forces acting on an object:
Vertical # of g-Forces: (FN / FgEarth)
Horizontal # of g-Forces: (ax / gEarth)
FN = The Normal Force an object has, such as that produced by rocket fuel when launching upward.
FgEarth = The gravitational force caused by the Earth.
ax = Acceleration of an object in the x-direction.
gEarth = The acceleration due to gravity of the Earth.
#
P. Rule .
Gravitational Fields:
A field in which a force of gravitational attraction is present. Diagrams are drawn as so:
 />
/>
The gravitational fields of the Earth and the Moon.
The lines are Field Lines, and the strength of the field is represented by how close the lines are to one another. Since all the lines are pointed internally the centers of mass of the moon and the Earth, they illustrate constant downward gravitational fields.
The farther away from the planet, as depicted in the diagram, the more distant the field lines, and thus the weaker the gravitational force acting on the object. For a single object, gravitational field lines are always toward the center of mass of the object.
The equation for a g.f. when it has a constant value, like on Earth (generalizing), is
g = Fg / m
In a constant gravitational field, any object will produce the gravitational acceleration constant using this equation. On Earth, this is 9.81 m/s².
The non-constant gravitational field equation, which can be used for the gravitational field of any object, is:
g = (G × mo) / r²
g = The Gravitational Field, e.g. the gravitational attraction a mass exerts on the surrounding area. For non-constant fields (all real ones as distance increases from the mass), the field refers to the force experienced by an object (at any location) due to the gravitational pull of the mass. It is measured in N/kg, which simplifies to m/s².
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
mo = Mass of the object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
A field in which a force of gravitational attraction is present. Diagrams are drawn as so:
 />
/>The lines are Field Lines, and the strength of the field is represented by how close the lines are to one another. Since all the lines are pointed internally the centers of mass of the moon and the Earth, they illustrate constant downward gravitational fields.
The farther away from the planet, as depicted in the diagram, the more distant the field lines, and thus the weaker the gravitational force acting on the object. For a single object, gravitational field lines are always toward the center of mass of the object.
The equation for a g.f. when it has a constant value, like on Earth (generalizing), is
g = Fg / m
In a constant gravitational field, any object will produce the gravitational acceleration constant using this equation. On Earth, this is 9.81 m/s².
The non-constant gravitational field equation, which can be used for the gravitational field of any object, is:
g = (G × mo) / r²
g = The Gravitational Field, e.g. the gravitational attraction a mass exerts on the surrounding area. For non-constant fields (all real ones as distance increases from the mass), the field refers to the force experienced by an object (at any location) due to the gravitational pull of the mass. It is measured in N/kg, which simplifies to m/s².
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
mo = Mass of the object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
#
P. Rule .
Universal Gravitational Potential Energy
Whereas before, the only equation for PEg (mgh) referred to objects in a constant gravitational field, recent advancements have led to the development of a Universal equation, which can provide the gravitational potential energy for any object in the universe, regardless of field:
Ug = -(G × m1 × m2) / (r)
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
m1 = Mass of the first object.
m2 = Mass of the second object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
As evident, the only differences between this equation and the Law of Gravitation is the negative and the r having a degree of '1' instead of '2'. While the equation for U.G.P.E. always produces a negative value, the change in U.G.P.E. can be positive. Furthermore, U.G.P.E. requires 2 objects to function.
Mixing and matching different forms of gravitational potential energy, such as in a conservation of mechanical energy, is forbidden. It is the law of the land. 'mgh' merely approximates the greater U.G.P.E. equation, and so must never be used alongside the greater equation in any circumstance.
You must only use one or the other. If which to use is ever in doubt (e.g., the object is leaving ground level), just use the U.G.P.E..
Whereas before, the only equation for PEg (mgh) referred to objects in a constant gravitational field, recent advancements have led to the development of a Universal equation, which can provide the gravitational potential energy for any object in the universe, regardless of field:
Ug = -(G × m1 × m2) / (r)
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
m1 = Mass of the first object.
m2 = Mass of the second object.
r = The distance between the centers of mass of the two objects, not the radius (unless it is by circumstance).
As evident, the only differences between this equation and the Law of Gravitation is the negative and the r having a degree of '1' instead of '2'. While the equation for U.G.P.E. always produces a negative value, the change in U.G.P.E. can be positive. Furthermore, U.G.P.E. requires 2 objects to function.
Mixing and matching different forms of gravitational potential energy, such as in a conservation of mechanical energy, is forbidden. It is the law of the land. 'mgh' merely approximates the greater U.G.P.E. equation, and so must never be used alongside the greater equation in any circumstance.
You must only use one or the other. If which to use is ever in doubt (e.g., the object is leaving ground level), just use the U.G.P.E..
# Binding Energy: The minimum energy or work necessary to completely remove one object from another object. This can be applied in both splitting an atom and launching a space rocket.
# Escape Velocity: The escape velocity of a planet is the minimum velocity at which an object can be launched and have it completely escape the gravitational attraction of a planet. If launched from the planet with a smaller velocity than the escape velocity, the object will eventually fall back to the planet.
The equation(s) for escape velocity (for any planet/celestial object) are:
$$ v_{\text{escape}} = \sqrt{\frac{2 G m_p}{R_p}} $$ $$ v_{\text{escape}} = \sqrt{2 a_p R} $$ G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
mp = Mass of the planet.
Rp = The Radius of the planet.
ap = The acceleration due to the gravitational pull of the planet on the body.
Choose whichever based on the variables you have. The first equation is derived as so. The second is more of a generalization, most applicable on the surface of a planet.
#
P. Rule .
The Principle of Superposition dictates the net gravitational force of one particle in a system of particles. The basic idea is that the gravitational forces acting on that specific particle, are individually computed from each of the other particles, and from there are summed.
The forces must always be summed vectorally, accounting for direction - see Rule 140.
The forces must always be summed vectorally, accounting for direction - see Rule 140.
#
P. Rule .
Internal Gravitation
Gravitational attraction INSIDE a planet, follows slightly different equations (though still derived from the base ones) that must be memorized. In doing this, 'r' will become less than the radius of the planet.
The Shell Theorem was formulated by Newton, and follows as so:
"A uniform spherical shell of matter attracts a particle that is outside the shell as if all the shell’s mass were concentrated at its center."
The Earth, and other planet/spherical celestial object, is a nest of shells, each shell individually attracting objects.
For the sake of the uber-idealized equations (that will determine the force of gravity while the object is inside the planet) working as accurately as possible, several assumptions need to be made:
An object traversing the Earth tunnel, with Earth meeting the three characteristics previously described. As the object goes deeper, its gravitational attraction will decrease as more mass becomes part of the outer shell, which does not act on the object (relatively).
Using a simple derivation, a revolutionary new equation can be determined for the gravitational force acting on any object that is within a planet:
Fg = (G × mo × mp × r) / R³
Fg = The force of gravitational attraction.
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
mo = Mass of the object.
mp = Mass of the planet/celestial body.
r = The distance of the object from the center of mass of the planet.
R = The actual radius of the planet.
Gravitational attraction INSIDE a planet, follows slightly different equations (though still derived from the base ones) that must be memorized. In doing this, 'r' will become less than the radius of the planet.
The Shell Theorem was formulated by Newton, and follows as so:
"A uniform spherical shell of matter attracts a particle that is outside the shell as if all the shell’s mass were concentrated at its center."
The Earth, and other planet/spherical celestial object, is a nest of shells, each shell individually attracting objects.
For the sake of the uber-idealized equations (that will determine the force of gravity while the object is inside the planet) working as accurately as possible, several assumptions need to be made:
- The planet, mp has a constant density.
- The object is capable of moving, without friction, through a tunnel drilled through the planet. Thus, the planet must also not be rotating.
- The only mass that causes a force on the object is the mass inside the sphere created by the object while it is radius r from the center. Thus, when the object is at the center, it will have no forces acting on it, and if it were 1 meter away, it will have a mass of radius 1 m exerting a gravitational force on it (see image).
"A uniform shell of matter exerts no net gravitational force on a particle located inside it."
While all the mass outside of r still causes a force of gravity on the object, because the force of gravity is proportional to the inverse square of the radius, all the forces of gravitational attraction outside of the internal sphere will cancel out.
An object traversing the Earth tunnel, with Earth meeting the three characteristics previously described. As the object goes deeper, its gravitational attraction will decrease as more mass becomes part of the outer shell, which does not act on the object (relatively).
Using a simple derivation, a revolutionary new equation can be determined for the gravitational force acting on any object that is within a planet:
Fg = (G × mo × mp × r) / R³
Fg = The force of gravitational attraction.
G = The Universal Gravitational Constant, or 6.67 x 10⁻¹¹ (N × m²) / (kg²).
mo = Mass of the object.
mp = Mass of the planet/celestial body.
r = The distance of the object from the center of mass of the planet.
R = The actual radius of the planet.
XI. Oscillations
XI.I Simple Harmonic Motion.
#
P. Rule .
A Simple Harmonic Motion system is one that will continue to oscillate back and forth forever in the absense of friction. The main two types of SHM are pendulums and springs.
Any force can cause simple harmonic motion, as long as it passes these two requirements:
# Simple Harmonic Motion from the perspective of the three base positions:Any force can cause simple harmonic motion, as long as it passes these two requirements:
- The force causing simple harmonic motion must be a restoring force.
- The magnitude of the restoring force must be proportional to the displacement from equilibrium position. For example, the Law of Elasticity (and thus all springs) follows this specification.
The initial position of the pendulum or spring weight being used for SHM, prior to being released, will be position 1. When released, the weight will move through position 2 (the rest position) and slow into position 3 (the maximum displacement on the other side of position 2). Afterwards, the weight will returns backward through position 2 into position 1, restarting the cycle.
The velocities at position one and three are equal to zero. The velocity is at its maximum at position two.
The acceleration will be linearly proportional to the spring force, meaning it follows the same pattern as the spring force. Thus, the magnitude of acceleration will be at its max at positions 1 & 3, while the acceleration at position 2 will be 0.
When moving toward rest position, acceleration and velocity are in the same direction and thus the weight is speeding up. When moving away from rest position, however, the weight will now be slowing down, as the acceleration is always pointed toward the rest position (as it is tied to the force) and velocity away from it.
#
P. Rule .
Simple Harmonic Motion is not Uniformly Accelerated Motion. You can't use the UAM equations for SHM. Live with it, punk.
# Amplitude: The magnitude of the maximum displacement from the equilibrium position, during simple harmonic motion.
#
P. Rule .
The difference between horizontal and vertical mass-spring systems lies solely in how the rest position changes in a vertical system due to gravity pulling the weight downward. In practice, the equations and everything will remain the same, vertically or horizontally, as the vertical system will still oscillate around that new rest point created by the weight.
#
P. Rule .
Pendulum Oscillation:
A pendulum is only considered to be in Simple Harmonic Motion when has an amplitude less than 15 degrees, as a result of the restoring force of pendulums. The restoring force for a pendulum is the component of gravity in the tangential direction, hereafter referred to as "the force of gravity tangential". This has the equation mgsin(θ).
θ being the angle made between the swing of the pendulum with the rest position. As the angle increases (e.g., the displacement from equilibrium position), the force of the gravity tangential increases. The force of gravity tangential is at 0 when the pendulum is at resting position.
As the angular displacement from rest position increases, the force of gravity tangential will increasingly point to a location below the rest position. This is patently not the rest position. Therefore, the force of gravity tangential is only a restoring force for small angles - namely, for oscillations where the amplitude < 15° (due to the small angle approximation - [[[[).
A pendulum is only considered to be in Simple Harmonic Motion when has an amplitude less than 15 degrees, as a result of the restoring force of pendulums. The restoring force for a pendulum is the component of gravity in the tangential direction, hereafter referred to as "the force of gravity tangential". This has the equation mgsin(θ).
θ being the angle made between the swing of the pendulum with the rest position. As the angle increases (e.g., the displacement from equilibrium position), the force of the gravity tangential increases. The force of gravity tangential is at 0 when the pendulum is at resting position.
As the angular displacement from rest position increases, the force of gravity tangential will increasingly point to a location below the rest position. This is patently not the rest position. Therefore, the force of gravity tangential is only a restoring force for small angles - namely, for oscillations where the amplitude < 15° (due to the small angle approximation - [[[[).
#
P. Rule .
In a mass-spring system, the displacement from the rest position is a linear displacement, ∆x.
In a pendulum system, the displacement from the rest position is an angular displacement, θ. This is the result of the pendulum oscillating through a small arc-length of a circle, given it is oscillating at its maximum extension. Use radians for the units.
In a mass-spring system, the displacement from the rest position is a linear displacement, ∆x.
In a pendulum system, the displacement from the rest position is an angular displacement, θ. This is the result of the pendulum oscillating through a small arc-length of a circle, given it is oscillating at its maximum extension. Use radians for the units.
#
P. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[
#
P. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[
#
P. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[