This is the second part of my complete notes for Classical Mechanics, covering topics of Dynamics such as Inertia, Force, the Laws of Motion, Equilibrium, Friction, Drag (more thoroughly than in Section III), and more. Due to the large scale of this topic, I have had to split even the complete notes into multiple parts.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Classical Mechanics, Part 2: Dynamics
Table Of Contents
VI. Force
VI.I Basics & Definitions.
# Inertial Mass: SCALAR. Mass is "the amount of matter in an object", according to various geeks and losers, but it is defined more precisely as the measure of inertia. Mass is a measure of an object's resistance to acceleration - therefore, the more mass an object has, the more it will resist acceleration.
There are other types of mass, such as gravitational mass, but they are in effect identical - this is known as the Equivalence Principle (see Rule [[[[[[[).
The S.I. unit for mass is the kilogram, while the Imperial unit for mass is the Slug (not the pound! That is a unit of force. See Rule 61 for more information).
#
P. Rule .
The most comprehensible and intuitive explanation of mass as a measurement of inertia and resistance to acceleration is as follows: A chair, which has little mass, is easy to accelerate from rest, while a desk, which has higher mass, is harder to accelerate and change the state of motion of from rest.
# Rest/Stationary: The state of motion in which an object is neither moving nor changing its position.
# Force: VECTOR.
Units: (kg)(m/s²), which is referred to as Newtons. The Imperial unit of force is the Pound.
Equation: See Rule 68.
Definition: A "push or pull", according to local fools and freaks, but it is better described as the ability to cause a change in the state of motion of an object. Force, Mass, and Acceleration are all connected - see Rule 74 for the Third Law of Motion.
Force is the ability to cause a change in the state of motion of an object, and acceleration is a state of motion while mass is a measurement of the tendency of an object to resist acceleration. For information regarding units, see Rule 61.
#
P. Rule .
A good visualization of force:
Take the classic pulley scenario, where you have a block attached to a string that goes over a pulley and attaches to a second block hanging in the air.
Fig. 1: A pulley diagram where mass 1 (in blue) is connected to the hanging mass 2 (in red).
If we were to add additional mass onto the hanging block, the force would increase, as dictated by the Second Law of Motion (see Rule 68):
Fig. 2: A pulley system with more mass added onto the hanging block, thus increasing the motion of the blocks.
This increase in force will increase the ability to cause acceleration, and so the acceleration for both blocks will increase. If we were to increase the mass of block 1, the resistance to change in the state of motion of the block will also increase, thus decreasing the motion of the two blocks:
Fig. 3: The movement of the blocks will decrease when more mass is add to the first block, because the resistance to the state of change caused by the second block (which has the force of gravity applied to it) will be greater.
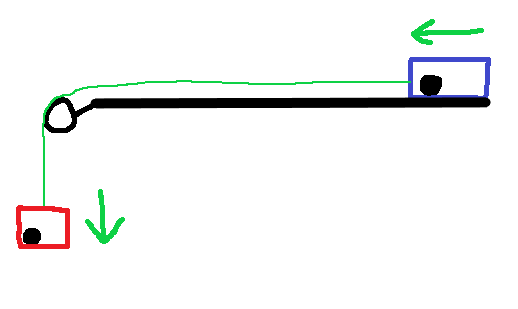
But what if we were to add so much weight to block 1 there would be no movement whatsoever? Why is it not moving?
Fig. 4: A pulley system where the first block is so overloaded with mass there is no movement.
The reason for this is Friction. When a block with mass is not accelerating despite having a horizontal force applied, it is the force of friction (see Rule 56) that is stopping it from moving, as it is being pressed into the table hard enough to balance out the leftward force.
If you return to the third figure, note that the acceleration of the blocks will be less than the acceleration of the blocks in Fig. 1, in spite of the fact that the blocks are evenly weighed. This is due to the increased friction being applied to the first block. Therefore, if you were to give the blocks equivalent weights and continue increasing the mass of those weights, then the acceleration of the blocks would continually decrease.
An individual force has the ability to cause a change in the state of motion of an object, but when other forces intervene (like friction), that force will do nothing.
Take the classic pulley scenario, where you have a block attached to a string that goes over a pulley and attaches to a second block hanging in the air.
Fig. 1: A pulley diagram where mass 1 (in blue) is connected to the hanging mass 2 (in red).
If we were to add additional mass onto the hanging block, the force would increase, as dictated by the Second Law of Motion (see Rule 68):
Fig. 2: A pulley system with more mass added onto the hanging block, thus increasing the motion of the blocks.
This increase in force will increase the ability to cause acceleration, and so the acceleration for both blocks will increase. If we were to increase the mass of block 1, the resistance to change in the state of motion of the block will also increase, thus decreasing the motion of the two blocks:
Fig. 3: The movement of the blocks will decrease when more mass is add to the first block, because the resistance to the state of change caused by the second block (which has the force of gravity applied to it) will be greater.
But what if we were to add so much weight to block 1 there would be no movement whatsoever? Why is it not moving?
Fig. 4: A pulley system where the first block is so overloaded with mass there is no movement.
The reason for this is Friction. When a block with mass is not accelerating despite having a horizontal force applied, it is the force of friction (see Rule 56) that is stopping it from moving, as it is being pressed into the table hard enough to balance out the leftward force.
If you return to the third figure, note that the acceleration of the blocks will be less than the acceleration of the blocks in Fig. 1, in spite of the fact that the blocks are evenly weighed. This is due to the increased friction being applied to the first block. Therefore, if you were to give the blocks equivalent weights and continue increasing the mass of those weights, then the acceleration of the blocks would continually decrease.
An individual force has the ability to cause a change in the state of motion of an object, but when other forces intervene (like friction), that force will do nothing.
#
P. Rule .
(2) Friction Force: VECTOR (a force).
Units: Newtons (because μ is dimensionless and FN is just a generic force)
Equation: Ffmax = μ × FN
Definition: The force opposing the sliding/rolling of an object across a surface. Friction, as a phenomenon, occurs due to the bonding on the atomic level between the object and the surface. Smooth surfaces cause less friction, because they have a lower surface energy and thus bond less with the object (given that the surface is flat, and all that matters is the texture).
If there is a problem that just states "friction" and does not define the type of friction or state of motion, just use the generic equation for friction, given above.
Ff, the force of friction itself, is ≤ μ × FN, and thus is equivalent to whatever force is pushing on it until it reaches Ffmax. For static friction, this is until it reaches Ffmax, which is the breakaway point from static friction to kinetic friction.
μ (myu) is the coefficient of friction. It is dimensionless, like radians. It can best be represented as the slope of the graph of kinetic/static friction vs. normal force, which represent how the friction increases for objects of differing masses.
The graph of the kinetic force of friction as the normal force (the apparent weight, see Rule 78) increases, as a result of increasing mass.
Units: Newtons (because μ is dimensionless and FN is just a generic force)
Equation: Ffmax = μ × FN
Definition: The force opposing the sliding/rolling of an object across a surface. Friction, as a phenomenon, occurs due to the bonding on the atomic level between the object and the surface. Smooth surfaces cause less friction, because they have a lower surface energy and thus bond less with the object (given that the surface is flat, and all that matters is the texture).
If there is a problem that just states "friction" and does not define the type of friction or state of motion, just use the generic equation for friction, given above.
Ff, the force of friction itself, is ≤ μ × FN, and thus is equivalent to whatever force is pushing on it until it reaches Ffmax. For static friction, this is until it reaches Ffmax, which is the breakaway point from static friction to kinetic friction.
μ (myu) is the coefficient of friction. It is dimensionless, like radians. It can best be represented as the slope of the graph of kinetic/static friction vs. normal force, which represent how the friction increases for objects of differing masses.
The graph of the kinetic force of friction as the normal force (the apparent weight, see Rule 78) increases, as a result of increasing mass.
# THE GREAT COMMANDMENTS OF FRICTION:
1. Kinetic Friction Force: Fk = μk × FN. The friction that acts between moving surfaces.
Static Friction Force: Fsmax = μs × FN. The force of friction on an object that's not moving.
2. Non-maximum static friction is Fs ≤ μs × FN, equal to whatever force is acting on it, as the third law of motion dictates. When that force becomes greater than the maximum static friction force, then kinetic friction becomes applied to the object instead. There is no maximum kinetic friction.
3. There is no way to theoretically derive the friction coefficient - it can only be found experimentally.
4. When you are measuring kinetic friction in the manner shown in the graph above, you would just measure the friction occurring as the object is sliding across the surface, and if you are measuring the static friction, you must find the friction that is required to get the object sliding in the first place (which will always be greater than the kinetic friction due to inertia).
5. Static frictional force can only match growing applied force - it can never surpass it. With more force being applied to an object, the static friction can only rise with it until the breakaway point where the object begins moving and the static friction becomes kinetic.
6. Static friction will always be higher then the kinetic friction, by inertia, so the kinetic friction you get when you finally get an object to start moving after pushing it will be less than the maximum static friction it just reached - the friction of the object will jump down, and you will be able to push it with less force than was needed to cause it to start moving. Experiment Website.
7. Rolling objects also work with static and kinetic friction. If the rolling object does not slip while moving, then it is undergoing static friction, and if it slips (slides) while moving, then it is momentarily using kinetic friction.
8. There are THREE subrules regarding THE DIRECTION OF THE FRICTION FORCE:
i) The force of friction is always parallel to the surfaces.
ii) Opposes sliding motion.
iii) Independent of the direction of the force applied.
#
P. Rule .
The fact that objects with more inertia (more massive) are harder to accelerate does NOT mean that there is some sort of "minimum force" required to accelerate objects with mass. Too much mass will NEVER prevent acceleration - you are simply imagining the friction of the ground (which is being pressed into the ground from the mass) prevented any sliding across its surface.
If you were, however, to imagine a perfectly smooth bowling ball moving down an infinite, smooth hallway with no air resistance, any amount of force would accelerate the bowling ball, no matter its size - it would just accelerate by a smaller amount the more massive it is.
If you were, however, to imagine a perfectly smooth bowling ball moving down an infinite, smooth hallway with no air resistance, any amount of force would accelerate the bowling ball, no matter its size - it would just accelerate by a smaller amount the more massive it is.
#
P. Rule .
a FORCE is a VECTOR. Thus, it has both magnitude and direction. Additionally, a force is always the result of an interaction between two objects. Examples:
- The Force of Gravity pulls everything toward the Earth. If you fall out of a tree, your fall is the result of an interaction between your body and the Earth.
- A car sliding to a stop is the result of a Friction Force, which was applied through an interaction between the tires and the ground.
- When a sled flies through the air and lands on the ground, it is the result of an applied force, created from the interaction between the sled and the ground.
#
P. Rule .
There are two types of force:
Contact Force:
The two interacting objects are touching.
Examples include the Applied Force ((5), see Rule 63 & Rule 64, between the two), the Drag Force ((1), see Rule 32), the Friction Force ((2), see Rule 56), the Normal Force ((4), see Rule 62), the Spring Force ((7), see Rule 81), and Tension ((6), see Rule 76, before).
Field Force / Action-at-a-distance:
The two interacting objects do not touch.
Examples include the Force of Gravity ((3), also known as weight, see the definition of the Force of Gravity), the Magnetic Force (see Rule [[[[[[[[), and the Electric Force ((8), see Rule 163).
This does not mean that the field forces can only be affecting an object if they are not touching - it only means that it can affect the object when they are not touching. Take Gravity, for example: When you fall through the air, gravity (your weight) is pulling you to the Earth, and it will continue pulling you to the ground when you have hit the ground.
Contact Force:
The two interacting objects are touching.
Examples include the Applied Force ((5), see Rule 63 & Rule 64, between the two), the Drag Force ((1), see Rule 32), the Friction Force ((2), see Rule 56), the Normal Force ((4), see Rule 62), the Spring Force ((7), see Rule 81), and Tension ((6), see Rule 76, before).
Field Force / Action-at-a-distance:
The two interacting objects do not touch.
Examples include the Force of Gravity ((3), also known as weight, see the definition of the Force of Gravity), the Magnetic Force (see Rule [[[[[[[[), and the Electric Force ((8), see Rule 163).
This does not mean that the field forces can only be affecting an object if they are not touching - it only means that it can affect the object when they are not touching. Take Gravity, for example: When you fall through the air, gravity (your weight) is pulling you to the Earth, and it will continue pulling you to the ground when you have hit the ground.
VI.II Free Body Diagrams and Basic Forces.
# Noninertial Frames: Reference frames in which Classical mechanics does not hold. Also known as noninertial reference frames.
# Force of Gravity (3): VECTOR.
Units: Newtons, as a generic force.
Equation: Fg = m × g
Definition: Fg, the attractive force that exists between the Earth (read: anything with mass) and an object. It is always directed straight downward, and is governed by the equation Fg = m × g, m being gravitational mass. Thus, gravity specifically can bypass the normal rules regulating the calculation of net force using the second law of motion as opposed to individual force. It is also synonymous with Weight, which is represented by 'W' if that is what you are choosing to use. Never confuse 'W' for weight with 'W' for work.
# Gravitational mass: SCALAR. The mass that helps determine the force of gravity that exists between an object and the Earth (or another body with mass). It is experimentally identifical to inertial mass - this is known as the Equivalence Principle ([[[[[[).
#
P. Rule .
The direction of gravity, which is caused by the Earth, is always toward the center of the planet, which is to say, down. The base S.I. units for gravity are (kg)(m/s²), which is given the unit of 'Newtons', a unit composed of other units.
#
P. Rule .
While the unit of force in S.I. units/the metric system is the Newton, the unit of force in the Imperial system is the Pound! The pound is defined as the amount of force needed to accelerated one Slug at one foot per second squared, Slug being the imperial unit of mass. A cool way to visualize the pound as a unit of force is to consider how if you were to be flying through the air at the speed of light, a piece of popcorn you would be holding in your hand would be tens of millions of pounds!
Because of the centuries of confusion over weight and mass, there are actually two types of pound, the pound-force and the pound-mass, because the goal of Science is to confuse the uninterested. To allow for some recompense from the horrible confusion that is the units of weight and mass, always assume that the pound is a unit of force unless otherwise stated. Dead-ringers for whether pound is in terms of force or mass include whenever the questions say something "weighs" 10 pounds or so, which is directly referencing force. Watch this video if ever confused - it will either confuse you further or resolve any immediate problems.
Kilograms and grams do not measure weight, because they do not measure a force. They merely measure the mass of the object, or the object's resistance to acceleration. Pounds, on the other hand, are a unit of mass multiplied by an acceleration, and so are a force.
Mass and weight differ in a billion ways - if you ever chance upon an ignoramus saying "I weigh 70 kilograms", or anything of the sort, respectfully inform them of their egregious error. If you were to go to a different planet, your weight would be different while your mass would remain the same. This is because mass is an Intrinsic Property, meaning it only depends on itself, an inherent characteristic. Weight on the other hand is an Extrinsic Property, determined by something external to the object, e.g. the acceleration due to gravity. You can also consider extrinsic properties to be composed properties, as stated before.
Because of the centuries of confusion over weight and mass, there are actually two types of pound, the pound-force and the pound-mass, because the goal of Science is to confuse the uninterested. To allow for some recompense from the horrible confusion that is the units of weight and mass, always assume that the pound is a unit of force unless otherwise stated. Dead-ringers for whether pound is in terms of force or mass include whenever the questions say something "weighs" 10 pounds or so, which is directly referencing force. Watch this video if ever confused - it will either confuse you further or resolve any immediate problems.
Kilograms and grams do not measure weight, because they do not measure a force. They merely measure the mass of the object, or the object's resistance to acceleration. Pounds, on the other hand, are a unit of mass multiplied by an acceleration, and so are a force.
Mass and weight differ in a billion ways - if you ever chance upon an ignoramus saying "I weigh 70 kilograms", or anything of the sort, respectfully inform them of their egregious error. If you were to go to a different planet, your weight would be different while your mass would remain the same. This is because mass is an Intrinsic Property, meaning it only depends on itself, an inherent characteristic. Weight on the other hand is an Extrinsic Property, determined by something external to the object, e.g. the acceleration due to gravity. You can also consider extrinsic properties to be composed properties, as stated before.
# Free Body Diagram: A graphic used to visualize the various forces working on an object at a particular instant. Occasionally known as a force diagram. Example.
# How to Draw a Free Body Diagram: Start by drawing a rudimentary image of your object and any important surroundings, such as any objects it is touching. If your object is moving, draw an image of your object at one specific instance during its motion. Here is a simple book, resting on a flat table:
Fig. 1: A simple drawing of a book on a table.
Next, draw a dot on the center of your object:
Fig. 2: The book on a table with the center of mass labeled.
This dot is called the Center of Mass, the location at which all the mass of an object is considered to be concentrated, like the nucleus of an atom. For an in-depth explanation, see Subsection VIII.I. Even if the mass is not concentrated in any particular point, such as an object with a constant mass density, the center of mass is in the middle of the object.
Next, we can begin drawing out the forces that are acting on our object, in this case the book. For one, the force of gravity is pushing the book downward. Make sure to never just write 'gravity', because you could be referring to either the force of gravity or acceleration due to gravity.
Fig. 3: The book with a force of gravity sign pointing downward.
If you have fastened your critical thinking cap correctly, you will know that this is not the complete diagram. If only the force of gravity were to be applied to the book, then the book would be in free fall, accelerating downward. However, we know the object not be in free fall since it is resting on a table. Therefore, there is an additional force at work preventing the book from accelerating downward. This force is the Normal Force (see Rule 62).
#
P. Rule .
(4) Normal Force: VECTOR (as a force).
Units: Newtons, as a generic force.
Equation: None. Sum the force acting in the y direction (on the tilted axes or otherwise) using the Second Law of Motion (see Rule 68) to create a problem-specific equation for the normal force.
Definition: The force exerted by the surface an object is resting on (perpendicular to said surface) as a result of the surface pushing against the object due to the Third Law of Motion, due to the force of gravity. The symbol for the normal force is FN.
This force is always perpendicular to the surface of which the object is resting, and is caused by that surface. A surface can never exert a pull on an object - thus, the normal force is always a push force.
The book with both the normal force and force of gravity labeled.
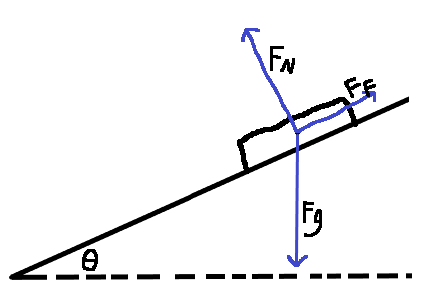
The Normal Force will change its direction if the object is on an incline, while the Force of Gravity will always be straight down:
The complete free body diagram of a book on an incline.
Of course, the Normal Force will always be perpendicular to the surface of which the object is on, so it will be perpendicular to the incline, in spite of the direction of the force of gravity. In addition, the force stopping the book from sliding down the incline is the force of Friction.
Units: Newtons, as a generic force.
Equation: None. Sum the force acting in the y direction (on the tilted axes or otherwise) using the Second Law of Motion (see Rule 68) to create a problem-specific equation for the normal force.
Definition: The force exerted by the surface an object is resting on (perpendicular to said surface) as a result of the surface pushing against the object due to the Third Law of Motion, due to the force of gravity. The symbol for the normal force is FN.
This force is always perpendicular to the surface of which the object is resting, and is caused by that surface. A surface can never exert a pull on an object - thus, the normal force is always a push force.
The book with both the normal force and force of gravity labeled.
The Normal Force will change its direction if the object is on an incline, while the Force of Gravity will always be straight down:
The complete free body diagram of a book on an incline.
Of course, the Normal Force will always be perpendicular to the surface of which the object is on, so it will be perpendicular to the incline, in spite of the direction of the force of gravity. In addition, the force stopping the book from sliding down the incline is the force of Friction.
#
P. Rule .
You must be very careful as to how you draw your arrows on free body diagrams. The arrows you draw are force vectors, and the length of the arrows represents the magnitude of those force vectors. When an object is stationary, the magnitude of the normal force and the magnitude of the force of gravity are the same.
# Applied Force (5): VECTOR (as a force).
Units: Newtons, as a generic force.
Equation: None. Sum the force acting in the whichever direction the applied force is acting (decomposing as needed, which would require summing in both directions) using the Second Law of Motion (see Rule 68) to create a problem-specific equation for the applied force.
Definition: The contact force applied by one object on another in an external fashion. A generic force that just is, rather than being explained away and categorized like the rest of the forces.
# Applied Force (5): VECTOR (as a force).
Units: Newtons, as a generic force.
Equation: None. Sum the force acting in the whichever direction the applied force is acting (decomposing as needed, which would require summing in both directions) using the Second Law of Motion (see Rule 68) to create a problem-specific equation for the applied force.
Definition: The contact force applied by one object on another in an external fashion. A generic force that just is, rather than being explained away and categorized like the rest of the forces.
#
P. Rule .
The vast majority of free body diagrams have to do with the interactions between multiple objects (as shown previously in section "How to Draw a Free Body Diagram" with only a table and a book). Now, to see how other forces can be displayed in a free body diagram, let's add a small block exerting a force of 5 Newtons on the book, which, although it is exerting a force on the book, is not causing the book to move:
Fig. 1: A block has been added to the diagram, exerting a force on the book.
Now, we must draw the forces caused by the block: There is the Force Applied by the block onto the book, but the book is not accelerating to the right. Indeed, even if it were accelerating rightward, there would still be another force at play: the Force of Friction (see Rule 56). As long as the surface on which an object is moving is not perfectly smooth, the force of friction will be pushing the object in the opposite direction. Adding these forces will give us the complete force diagram:
Fig. 2: The majority of the forces have been added to the diagram, sans one.
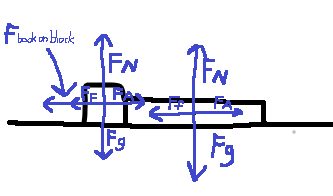
Very important: There is still one force that hasn't been added to the diagram. As known from the third law of motion (see Rule 74), every action has an equal and opposite reaction. Thus, when the block is pushing on the book, the book is pushing back on the block with an equal force. See Rule 74 for why the block and the book are still able to move, even though they are pushing against each other with equal & opposite forces.
Thus, the block will have the force of the book pushing back against it, which will not affect the net forces of the book:
Fig. 3: The completed force diagram. Force Vectors not drawn to scale.
Of course, the Force Fbook on block is equivalent to -FA.
Fig. 1: A block has been added to the diagram, exerting a force on the book.
Now, we must draw the forces caused by the block: There is the Force Applied by the block onto the book, but the book is not accelerating to the right. Indeed, even if it were accelerating rightward, there would still be another force at play: the Force of Friction (see Rule 56). As long as the surface on which an object is moving is not perfectly smooth, the force of friction will be pushing the object in the opposite direction. Adding these forces will give us the complete force diagram:
Fig. 2: The majority of the forces have been added to the diagram, sans one.
Very important: There is still one force that hasn't been added to the diagram. As known from the third law of motion (see Rule 74), every action has an equal and opposite reaction. Thus, when the block is pushing on the book, the book is pushing back on the block with an equal force. See Rule 74 for why the block and the book are still able to move, even though they are pushing against each other with equal & opposite forces.
Thus, the block will have the force of the book pushing back against it, which will not affect the net forces of the book:
Fig. 3: The completed force diagram. Force Vectors not drawn to scale.
Of course, the Force Fbook on block is equivalent to -FA.
#
P. Rule .
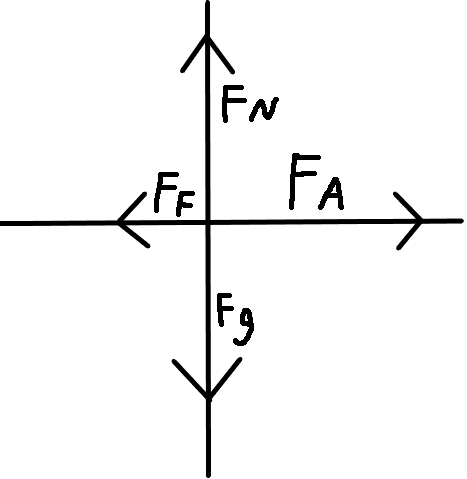
Many a time, the free body diagrams will be separated into individual graphs for each object. Continuing from a previous example (see Rule 64), this can be done for the book as so:
Fig. 1: A complete free body diagram for book, given its own axes.
Fig. 1: A complete free body diagram for book, given its own axes.
#
P. Rule .
All free-body diagrams are idealized. The only force that starts at the center of mass is the Force of gravity, while the others have different starting points.
The Force of Friction starts below the center of mass on the surface the object is laying upon, the Force Applied is starting from the object applying the force and points toward the center of mass, and the Normal Force points perpendicular from the surface the object is on. This more 'correct' way of drawing free body diagrams will be utilized when drawing diagrams for Torque (see Rule 139).
The Force of Friction starts below the center of mass on the surface the object is laying upon, the Force Applied is starting from the object applying the force and points toward the center of mass, and the Normal Force points perpendicular from the surface the object is on. This more 'correct' way of drawing free body diagrams will be utilized when drawing diagrams for Torque (see Rule 139).
VI.III Laws of Motion.
#
P. Rule .
The First Law of Motion:
"An object at rest will remain at rest and an object in motion will maintain a constant velocity unless acted upon by a net external force."
This law is also known as the Law of Inertia.
As you should see, there are two cases being described by this rule. First, if you were to have a pebble on the ground at rest, you would be able to conclude that there is no net external force acting on the rock. This almost never means that there is NO force acting on the rock, but rather that all of the forces acting in any particular direction cancel eachother out, making there be no net external force. This is mathematically represented as follows:
ΣFy = FN + Fg = 0
The second case is that of an object in motion maintaining a constant velocity unless acted upon by a net external force. If you had a ball rolling across a flat frictionless surface, the only thing that would ever cause it to slow down and eventually stop is air resistance. Without air resistance, it would continue rolling at the same velocity forever.
If there were to be a block (at rest) standing in the direction that the ball is rolling, when the ball hits the block, a reaction force with the equivalent magnitude to the force with which the sphere hit the block will cause a net external force to slow down the ball and push the block momentarily, until the ball has completely lost acceleration and velocity, transferring these attributes to the block through the Force Applied.
"An object at rest will remain at rest and an object in motion will maintain a constant velocity unless acted upon by a net external force."
This law is also known as the Law of Inertia.
As you should see, there are two cases being described by this rule. First, if you were to have a pebble on the ground at rest, you would be able to conclude that there is no net external force acting on the rock. This almost never means that there is NO force acting on the rock, but rather that all of the forces acting in any particular direction cancel eachother out, making there be no net external force. This is mathematically represented as follows:
ΣFy = FN + Fg = 0
The second case is that of an object in motion maintaining a constant velocity unless acted upon by a net external force. If you had a ball rolling across a flat frictionless surface, the only thing that would ever cause it to slow down and eventually stop is air resistance. Without air resistance, it would continue rolling at the same velocity forever.
If there were to be a block (at rest) standing in the direction that the ball is rolling, when the ball hits the block, a reaction force with the equivalent magnitude to the force with which the sphere hit the block will cause a net external force to slow down the ball and push the block momentarily, until the ball has completely lost acceleration and velocity, transferring these attributes to the block through the Force Applied.
#
P. Rule .
The Second Law of Motion:
ΣF = m × a
An integrable part of all force equations, and is used in variated forms by some forces (example: the force of gravity is m × g, g being the acceleration due to gravity).
Note that the force is the NET force, not any individual force. Therefore, when you have multiple forces in the free body diagram, you can't just use this equation to find each force - you have to incorporate the knowledge of each force to find the other forces, because they effect eachother. You can, however, isolate net force in the x and y directions.
When the motion is in one direction, you can separate the forces into Fwest and Feast, and when it is split into two dimensions, then you can only separate the forces into Fx and Fy. Therefore, once you decompose the forces to be one-dimensional, you can use the Second Law of Motion on either side. Master physicist hackz.
For a modern 21st century™ version of the 2nd law that incorporates momentum, see here.
ΣF = m × a
An integrable part of all force equations, and is used in variated forms by some forces (example: the force of gravity is m × g, g being the acceleration due to gravity).
Note that the force is the NET force, not any individual force. Therefore, when you have multiple forces in the free body diagram, you can't just use this equation to find each force - you have to incorporate the knowledge of each force to find the other forces, because they effect eachother. You can, however, isolate net force in the x and y directions.
When the motion is in one direction, you can separate the forces into Fwest and Feast, and when it is split into two dimensions, then you can only separate the forces into Fx and Fy. Therefore, once you decompose the forces to be one-dimensional, you can use the Second Law of Motion on either side. Master physicist hackz.
For a modern 21st century™ version of the 2nd law that incorporates momentum, see here.
#
P. Rule .
Whenever you are doing force problems, there is a very high likelihood you will need to sum the forces acting in the x, y, and possibly z directions of the object. Thus, given an object resting upon a flat horizontal surface with a mass of 1627 grams, a Force of Friction of 3.6 N, and a Force Applied of 5.0 N, the free body diagram would look something like this:
Fig. 1: A complete free body diagram for book, given its own axes.
Summing Forces is always conducted as follows: Right minus left, up minus down, or inward minus outward.
We can immediately determine the net force in the x-direction from the applied force and the force of friction:
ΣFx = FA - FF
ΣFx = 5.0 N - 3.6 N
If the question requires you to determine every force acting upon the object, you cannot neglect finding the value of the force of gravity because it is canceled out by the normal force. In this case, m × g equals (1.627 kg) × (-9.81 m/s²) ≈ 16 N. Summing the forces in y-direction goes as follows:
ΣFy = FN - Fg
Additionally, the second law of motion can be utilized to create a simpler, more generalized equation for both the x and y directions:
ΣFy = m × ay
ΣFx = m × ax
Thus, we can determine that the force in the y-direction is equal to 0, since FN - Fg = 16 - 16. Note that summing forces will get more complicated when the forces are not in perfect 90° directions, such as in the incline example (see Rule 62). When this is the case, vector decomposition is required - this how m × ay is the force in the y-direction even if the normal force is tilted.
Fig. 1: A complete free body diagram for book, given its own axes.
Summing Forces is always conducted as follows: Right minus left, up minus down, or inward minus outward.
We can immediately determine the net force in the x-direction from the applied force and the force of friction:
ΣFx = FA - FF
ΣFx = 5.0 N - 3.6 N
If the question requires you to determine every force acting upon the object, you cannot neglect finding the value of the force of gravity because it is canceled out by the normal force. In this case, m × g equals (1.627 kg) × (-9.81 m/s²) ≈ 16 N. Summing the forces in y-direction goes as follows:
ΣFy = FN - Fg
Additionally, the second law of motion can be utilized to create a simpler, more generalized equation for both the x and y directions:
ΣFy = m × ay
ΣFx = m × ax
Thus, we can determine that the force in the y-direction is equal to 0, since FN - Fg = 16 - 16. Note that summing forces will get more complicated when the forces are not in perfect 90° directions, such as in the incline example (see Rule 62). When this is the case, vector decomposition is required - this how m × ay is the force in the y-direction even if the normal force is tilted.
#
P. Rule .
When a question asks you to find the acceleration of an object given some forces, it is asking you to recompose the acceleration vector using the x and y direction accelerations. If the object is at rest, the y-direction acceleration is zero.
#
P. Rule .
Whenever two bodies move together, such as in pulley problems where the two masses are connected by a string, the bodies have the same acceleration and are thus called the System. Since the bodies have the same acceleration, they need to share the same sign, although the mass hanging is moving downward. The direction of the system will thus be identified as positive, known as "String direction".
#
P. Rule .
Because mass is a scalar and force is a vector, by the second law of motion, net force and acceleration are in the same direction. Velocity and acceleration, however, are not always in the same direction. Only if velocity initial is zero would velocity and acceleration be in the same direction.
#
P. Rule .
You cannot combine unit vectors and magnitude in the same equation. All vectors must be either written in unit vector form or broken down into their components in the perpendicular directions. The UAM equations require that all units be in terms of the x or y directions. Always make sure that everything you're plugging into the equation is in the same perfect x or y direction.
#
P. Rule .
The Third Law of Motion:
"For every action, the reaction will be equal in magnitude but opposite in direction."
If the forces in a particular direction cancel out, that just means that there is no acceleration in that direction. The object is in equilibrium, and that can mean that it is not moving or that it is moving at a constant velocity.
Take terminal velocity, for example: the drag force is equal to the force of gravity, and yet the object remains falling. It just has no acceleration.
.
.
.
Every force is the result of an interaction between two objects, and the forces or these objects are known as a Third Law Force Pair, or a aCTiOn-ReAcTiON PaiR according to various well-to-do ignoramuses and leading textbook publishers. This can be represented by the following equation:
Fab = -Fba
- Where a and b are the different objects.
For example: If you are to strike a nail with a hammer, the force pair would be the hammer and the nail. The nail starts at rest, and when the hammer strikes the nail, the nail accelerates and has a force applied to it by the hammer. Inversely, the hammer accelerates at the beginnning and accelerates in the opposite direction after hitting the nail.
When a car crashes into a building and the building does not move, that is because the mass of the building (the level of resistance the building has to acceleration) is large enough to prevent the force exerted by the car from changing its state of motion.
"For every action, the reaction will be equal in magnitude but opposite in direction."
THE KEY TO THE PUZZLE:
If the forces in a particular direction cancel out, that just means that there is no acceleration in that direction. The object is in equilibrium, and that can mean that it is not moving or that it is moving at a constant velocity.
Take terminal velocity, for example: the drag force is equal to the force of gravity, and yet the object remains falling. It just has no acceleration.
.
.
.
Every force is the result of an interaction between two objects, and the forces or these objects are known as a Third Law Force Pair, or a aCTiOn-ReAcTiON PaiR according to various well-to-do ignoramuses and leading textbook publishers. This can be represented by the following equation:
Fab = -Fba
- Where a and b are the different objects.
For example: If you are to strike a nail with a hammer, the force pair would be the hammer and the nail. The nail starts at rest, and when the hammer strikes the nail, the nail accelerates and has a force applied to it by the hammer. Inversely, the hammer accelerates at the beginnning and accelerates in the opposite direction after hitting the nail.
When a car crashes into a building and the building does not move, that is because the mass of the building (the level of resistance the building has to acceleration) is large enough to prevent the force exerted by the car from changing its state of motion.
#
P. Rule .
While the normal force and the force of gravity of, say, a book in the horizontal resting state are equivalent in magnitude and working in the opposite directions (FN = -Fg), they are NOT third law force pairs. This is because the two forces act on the same object, while force pairs must be between two objects. Instead, one must consider whatever surface the book is laying upon, whether it be a table or the earth, for the second object of the force pair. On the surface the book is laying on, there is a downward normal force caused by the book as the complementary force pair to the upward normal force of the book, which is caused by the table. All Normal forces are the result of a third law force pair, you just need to find the second object.
VI.IV More Introductory Forces.
Units: Newtons, as a generic force.
Equation: None. Sum the force acting in the whichever direction the applied force is acting (decomposing as needed, which would require summing in both directions) using the Second Law of Motion (see Rule 68) to create a problem-specific equation for the tension force.
Definition: FT, the force transmitted through a rope, cable, string or wire pulled taut by forces acting on both ends.
Any object that will go slack if not pulled taut will cause a tension force. The tension force of one side of the rope is always pointed toward the other side of the rope. Thus, the tension force is always a pull and is in opposite directions on the ends of the rope.
The magnitude of the tension force on both ends of the rope are the same, regardless of there being a pulley or not. If the acceleration is the same on either end (and can be visualized as such), the tension is with the same force at either end.
Many questions will directly ask you to "find the tension" of a wire or rope, which is just ignoramus-speak for "find the value of the tension force".
#
P. Rule .
For every single pulley problem, imagine that the all of the forces are just acting in one direction, because the tension of the rope is going to be the same on either side of the pulley. This direction will be whatever direction the forces are moving with respect to gravity (e.g. downward) or the applied force. If needs be, draw the conceptual free body diagram with mg pulling in the x direction, even though this violates the purity of the diagram by not pointing the gravity force vector directly downward. It all helps with visualization, purely, and when the forces are acting on inclines, adjust the axes with which you are making the system one-dimensional as needed.
# FACTS and LOGIC needed for Physics work - Tension Edition:
When different objects are being dragged across a surface by a force, each object connected by a massless wire, they all have the same acceleration. This can be determined in the field without any memorization - just imagine a train starting up, and how each part of the train will start moving with the same acceleration.
In order to find the force of the tension of any particular wire in the sequence of connected objects, you need to use the mass of all of the objects that the wire is pulling, even the ones that are not directly connected to the wire, but are instead several objects separated through different wires. This makes quite a bit of sense when you think about it for a second. Watch.
# Translational Equilibrium: The state of an object when the net force acting on an object is equal to zero. This occurs when an object either has 1. constant velocity, or is 2. at rest.
#
P. Rule .
Although translational equilibrium requires the net forces of an object to be zero, this does not necessarily mean that the object is at rest:
The net force of an object is the mass multiplied by acceleration. Acceleration, at least the average acceleration used in the equation, is equal to the change in velocity divided by the change in time. Therefore, if there is a constant velocity (thus having the 'change in velocity' equal zero), the acceleration will equal zero and thus net force. This is the circumstance in which an object can be in equilibrium without being at rest - when the object is under constant velocity.
The net force of an object is the mass multiplied by acceleration. Acceleration, at least the average acceleration used in the equation, is equal to the change in velocity divided by the change in time. Therefore, if there is a constant velocity (thus having the 'change in velocity' equal zero), the acceleration will equal zero and thus net force. This is the circumstance in which an object can be in equilibrium without being at rest - when the object is under constant velocity.
#
P. Rule .
You do NOT feel the force of gravity acting on you - you do not feel your weight. When you stand on a scale, it is not actually measuring the force of gravity on you, but rather the downward force that is being applied to it. In effect, it is measuring the upward normal force the scale is acting on you, which is also known as the apparent weight. This is why when you move about on the scale, it changes weight, even though your gravitational force on Earth always remains the same.
When you are at rest, your acceleration in the y-direction equals zero and so your normal force equals your weight. Therefore, when you are at rest, your apparent weight and actual weight are the same. Mathematically, this is all described as follows, where we know FN to be equal to one's apparent weight:
FN = Fg + m × ay
If a > 0, then m × ay > 0 and FN > Fg
If a = 0, then m × ay = 0 and FN = Fg
If a < 0, then m × ay < 0 and FN < Fg
If one were to fall from the top of a building within an elevator, they would feel weightless the whole way down. This is apparent weightlessness, and occurs when the individual and the container are falling at the same rate. Mathematically, it is proved as follows:
In free fall, ay = -g
FN = Fg + m × ay
FN = m × g + m × (-g)
FN = m × (g - g)
FN = m × (0)
FN = 0
When you are at rest, your acceleration in the y-direction equals zero and so your normal force equals your weight. Therefore, when you are at rest, your apparent weight and actual weight are the same. Mathematically, this is all described as follows, where we know FN to be equal to one's apparent weight:
FN = Fg + m × ay
If a > 0, then m × ay > 0 and FN > Fg
If a = 0, then m × ay = 0 and FN = Fg
If a < 0, then m × ay < 0 and FN < Fg
If one were to fall from the top of a building within an elevator, they would feel weightless the whole way down. This is apparent weightlessness, and occurs when the individual and the container are falling at the same rate. Mathematically, it is proved as follows:
In free fall, ay = -g
FN = Fg + m × ay
FN = m × g + m × (-g)
FN = m × (g - g)
FN = m × (0)
FN = 0
#
P. Rule .
When in doubt, make a free body diagram and start summing forces. If anything, it will give you a value to plug into another equation. Always go through the motions of the four steps of free body diagrams if you run into trouble:
1) Draw Free Body Diagram.
2) Break Forces into Components.
3) Redraw Free Body Diagram.
4) Sum the Forces in the x and y directions.
1) Draw Free Body Diagram.
2) Break Forces into Components.
3) Redraw Free Body Diagram.
4) Sum the Forces in the x and y directions.
#
P. Rule .
When you are solving symbolically, it is totally okay to plug in 'symbolic numbers', like 0, in to make substitution easier later on. It is the more exact, problem-specific numbers that you put off plugging in until the end.
VI.V Spring Force.
# Equilibrium Position: The position in which the spring is at rest before a force is applied to the spring.
#
P. Rule .
Spring Force (7): VECTOR (as a force).
Units: Newtons, as a generic force.
Equation: Fs = -k × ∆x
Fs = Force caused by spring.
k = Spring constant.
∆x = The displacement of the spring from the equilibrium position or rest position.
Definition: The spring force is the force exerted by a spring as it is being expanded or compressed. Spring force is a restoring force, because it will always point back to the resting position when it is expanded or compressed.
Spring force is linearly proportional to the distance the spring is compressed or expanded to, because of Hooke's Law, also known as the Law of Elasticity, which is mathematically defined above.
The Spring Constant, sometimes referred to as the "force constant" or "proportionality constant" of the spring force, is the magnitude of the slope of the line created by the spring force as a function of the displacement graph. This is a slope-type constant similar to kinetic and static friction (see Rule 56 for more.) The units for the spring constant are (Newtons / meters).
A large spring constant requires a larger force to compress the spring to the same displacement from rest position. A smaller spring constant requires a smaller force to compress the spring to the same displacement from equilibrium position.
The negative in the law of elasticity indicates that the direction of the spring force is opposite to the direction of the displacement of the spring from equilibrium position.
Units: Newtons, as a generic force.
Equation: Fs = -k × ∆x
Fs = Force caused by spring.
k = Spring constant.
∆x = The displacement of the spring from the equilibrium position or rest position.
Definition: The spring force is the force exerted by a spring as it is being expanded or compressed. Spring force is a restoring force, because it will always point back to the resting position when it is expanded or compressed.
Spring force is linearly proportional to the distance the spring is compressed or expanded to, because of Hooke's Law, also known as the Law of Elasticity, which is mathematically defined above.
The Spring Constant, sometimes referred to as the "force constant" or "proportionality constant" of the spring force, is the magnitude of the slope of the line created by the spring force as a function of the displacement graph. This is a slope-type constant similar to kinetic and static friction (see Rule 56 for more.) The units for the spring constant are (Newtons / meters).
A large spring constant requires a larger force to compress the spring to the same displacement from rest position. A smaller spring constant requires a smaller force to compress the spring to the same displacement from equilibrium position.
The negative in the law of elasticity indicates that the direction of the spring force is opposite to the direction of the displacement of the spring from equilibrium position.
# Spring Work:
If an object is attached to the spring’s free end, the work WS (see Subsection VII.I) done on the object by the spring force when the object is moved from an initial position xi to a final position xf is as follows:
Ws = 1/2 × k × ∆x²
This is the result of taking the integral of the non-constant spring force, since the Law of Elasticity dictates that the force of the spring changes depending on displacement.
Work Ws is positive if the block ends up closer to the relaxed position (x = 0) than it was initially. It is negative if the block ends up farther away from x = 0. It is zero if the block ends up at the same distance from x = 0.
#
P. Rule .
The Law of Elasticity is only applicable on a spring until it reaches the Elastic limit, the maximum displacement a spring can undergo until the spring will be permanently deformed.
#
P. Rule .
When you are using the spring force equation in a free body diagram, you only use the negative of the equation to determine the direction of the spring. IMMEDIATELY disregard the negative when you go into calculations. Carry out all of the calculations with "k × ∆x" for the spring force. This is a very strange rule and thing to do, but it is tradition and is immutable.
#
P. Rule .
The spring constant of a spring can differ when the spring is horizontal or vertical - this is because of gravity. The force of gravity acting on the center of mass of a vertically hanging spring can make a spring longer, while that same spring laid down horizontally would be shorter. Furthermore, a spring standing horizontally would compress a little and be shorter, all due to the inherent gravity of the spring that is always neglected in calculations.
VII. Energy and Work
VII.I Basics of Work.
Units: "Newton-Meters", known as Joules.
Equation:
These are for work done under a constant force. If the force is not constant, see Rule 86.
W = F × d × cos(θ) - General
W = F × ∆r × cos(θ) - With respect to vectors
W = F · ∆r - With respect to the Dot Product
W = ∆KE - With respect to the Kinetic Energy
F = The magnitude of the Force doing work on the object.
d = The magnitude of the Displacement of the force.
∆r = The change in position of an object in three dimensional space, using unit vectors.
θ = Angle between F & d. Always use a positive number.
Definition: The energy transferred to or from an object through the application of a force that caused displacement in the object. Because work is based on displacement, it is completely independent of the path of an object.
Work is a result of the dot product between Force and displacement. As before, the dot product is the magnitude of one vector times the magnitude of the tip-to-tail placement of the second vector onto the first vector. People may refer to this as the "projection" of the second vector onto the first vector.
The 'net work' is the sum of the individual works of each force - if you want, you can combine all of the forces into the net force using vector decomposition and then recomposition, and then get the work from there.
#
P. Rule .
Every force that is being applied to the object is producing its own work on the object, whether positive or negative.
Important: The direction of the force being applied is totally independent of the direction of the displacement of the object. If you hold an object and slowly move it downward, you are still applying a positive force on the object.
Important: The direction of the force being applied is totally independent of the direction of the displacement of the object. If you hold an object and slowly move it downward, you are still applying a positive force on the object.
#
P. Rule .
Work as a Non-Constant Force:
$$W = \int_{x_i}^{x_f} F_x \, dx$$
Use with discretion. Whenever you see force with a variable, you must immediately recognize that it is a non-constant force, and that it will need to be integrated.
$$W = \int_{x_i}^{x_f} F_x \, dx$$
Use with discretion. Whenever you see force with a variable, you must immediately recognize that it is a non-constant force, and that it will need to be integrated.
#
P. Rule .
Gravity acts separately than the other forces with respect to work. Instead of using the total displacement and having θ act respective to it, the displacement for gravitational work is only vertical displacement, because gravity works strictly in the vertical direction, a quality other forces do not share. This is a result of gravity being a conservative force - see Subsection VII.IV for more information.
Gravity acts separately than the other forces with respect to work. Instead of using the total displacement and having θ act respective to it, the displacement for gravitational work is only vertical displacement, because gravity works strictly in the vertical direction, a quality other forces do not share. This is a result of gravity being a conservative force - see Subsection VII.IV for more information.
VII.II Power.
Units: (Joules / Seconds), known as Watts.
Equation: Consider the following equations in the same vein as how one may consider velocity.
(dW / dt) - The time derivative of work.
F × v - Alternate definition: if you use instantaneous velocity, you will get Instantaneous Power, and if you use average velocity, you will get Average Power. Only valid for constant forces.
(W / ∆t) - Average power.
Definition: The rate of doing or work or of transferring energy. It is the derivative of work.
# Horsepower: The amount of power that can be done by one horse. It is about 746 watts.
VII.III Mechanical Energy.
# Mechanical Energy: The sum of the potential and kinetic energy. All forms of potential energy are recognized under the tent of 'potential energy', including gravitational and elastic potential energy. Within an isolated system (where no outside force can interfere with the energy of the system), mechanical energy will remain constant, known as the Conservation of Mechanical Energy (see below).
# Conservation of Mechanical Energy: Energy can be transformed from one type to another (from potential to kinetic or vice versa) and transferred from one object to another, but as long as there are no nonconservative forces removing energy from the system (like friction, heat, or light), the total amount of energy within the system is always the same. E.g., MEi = MEf.
For example, when you drop a ball, at the point of release there will only be potential energy (specifically gravitational potential) in the ball-ground system, and no kinetic energy. As the ball falls, that energy will be converted into kinetic energy perfectly so that the total amount of energy always stays the same, and when the ball hits the ground, there will be no potential energy left (since the 'h' of 'mgh' (g.p.e.) will be 0), and the mechanical energy will now solely consist of kinetic energy.
This law holds only within an ISOLATED system, with no outside forces interfering with the energy of the system. An isolated system is "a physical system removed from other systems so that it does not interact with them". Thus, mechanical energy is conserved as long as no energy is converted to heat, light, or sound energy via work done by friction or whatnot, and no energy is added or removed from the system via work done by a force applied.
Thus, WFriction = 0, and WFa = 0 for mechanical energy to be conserved.
There is no real situation in which a system is isolated, because of air resistance and whatnot, but it can get fairly close - a pendulum will move back and forth to points almost at the previous height it reached, but always slightly less.
#
P. Rule .
Kinetic Energy: SCALAR.
Units: Joules.
Equation: The equation for it is derived from the non-constant work equation:
KE = (1/2) × m × v²
m = Mass
v = Velocity
Definition: The energy associated with the motion of the object. It can never be negative, and only ever exists when an object is in motion. If the object is not in motion, such as when an object pauses in mid-air after being thrown directly upward, then the object has no kinetic energy (all converted into potential energy if energy is conserved in the system).
Note that this equation is mutable to change into equivalent (though alternate) forms, such as Rotational Kinetic Energy (Rule 122), which uses angular velocity in place of linear velocity.
Units: Joules.
Equation: The equation for it is derived from the non-constant work equation:
KE = (1/2) × m × v²
m = Mass
v = Velocity
Definition: The energy associated with the motion of the object. It can never be negative, and only ever exists when an object is in motion. If the object is not in motion, such as when an object pauses in mid-air after being thrown directly upward, then the object has no kinetic energy (all converted into potential energy if energy is conserved in the system).
Note that this equation is mutable to change into equivalent (though alternate) forms, such as Rotational Kinetic Energy (Rule 122), which uses angular velocity in place of linear velocity.
# Rigid Body: A solid object that does not deform or change shape when external forces are applied. Thus, a spring is not a rigid body, due to the Elastic Limit. All 'Rigid bodies/objects with shape' are are just objects that do not change shape and are larger than point particles.
#
P. Rule .
Work–Kinetic energy theorem: Kinetic Energy and Work are both measurements of energy in Joules. An increase in the kinetic energy of a rigid body is caused by an equal amount of positive work done on the body by the net force acting on that body. Conversely, a decrease in kinetic energy is caused by an equal amount of negative work done by the net force.
Despite what the elites will tell you, there IS an assumption built into this theorem: the constancy of mass/inertia. An example where the Work-Energy Theorem fails (due to this assumption) is in rocket mechanics because such systems' masses change with time. It is here that the currently undiscovered principle of momentum comes into play, as detailed in Subsection VIII.II.
Despite what the elites will tell you, there IS an assumption built into this theorem: the constancy of mass/inertia. An example where the Work-Energy Theorem fails (due to this assumption) is in rocket mechanics because such systems' masses change with time. It is here that the currently undiscovered principle of momentum comes into play, as detailed in Subsection VIII.II.
#
P. Rule .
When dealing with a graph of the force acting on an object moving over a displacement, that would be the exact situation in which you can sum the area underneath the curve in order to find work: When the force is not a constant, integrating a Force vs. Displacement graph will give you work.
From this graph, you can determine a lot of things, including the 1. greatest and lowest kinetic energy, the 2. greatest and lowest speed of the object, and the 3. points at which it is at zero speed.
ALWAYS remember that Work is just the change in Kinetic Energy, so you must always sum the areas beginning at ∆r = 0. In other words, the first limit of integration, no matter what the second is (e.g. what point you pick on the graph), is zero.
1. By the Work–Kinetic energy theorem (see Rule 89), the kinetic energy is greatest where the work is greatest and thus inversely is lowest where the work is lowest, and thus the point on the graph where there is the greatest area of positive work (when the area of the force over the displacement is summed through integration) would be the point at which the kinetic area is greatest. The point on the graph with the greatest area of NEGATIVE work (summed negative force) will have the lowest kinetic energy.
2. By simple deduction from the equation for Kinetic Energy ((1/2) × m × v²), the higher the kinetic energy, the higher the speed, and so the highest speed/velocity will be at the point at which kinetic energy is greatest, and the lowest speed/velocity will be at the point at which kinetic energy is lowest.
3. The speed/velocity will be at zero when the kinetic energy will be at zero, which will be when the work is zero, which will be when the areas of the positive work and negative work cancel out.
From this graph, you can determine a lot of things, including the 1. greatest and lowest kinetic energy, the 2. greatest and lowest speed of the object, and the 3. points at which it is at zero speed.
ALWAYS remember that Work is just the change in Kinetic Energy, so you must always sum the areas beginning at ∆r = 0. In other words, the first limit of integration, no matter what the second is (e.g. what point you pick on the graph), is zero.
1. By the Work–Kinetic energy theorem (see Rule 89), the kinetic energy is greatest where the work is greatest and thus inversely is lowest where the work is lowest, and thus the point on the graph where there is the greatest area of positive work (when the area of the force over the displacement is summed through integration) would be the point at which the kinetic area is greatest. The point on the graph with the greatest area of NEGATIVE work (summed negative force) will have the lowest kinetic energy.
2. By simple deduction from the equation for Kinetic Energy ((1/2) × m × v²), the higher the kinetic energy, the higher the speed, and so the highest speed/velocity will be at the point at which kinetic energy is greatest, and the lowest speed/velocity will be at the point at which kinetic energy is lowest.
3. The speed/velocity will be at zero when the kinetic energy will be at zero, which will be when the work is zero, which will be when the areas of the positive work and negative work cancel out.
# Potential Energy: The energy stored in an object that has the potential to turn into different types of energy, such as kinetic energy.
#
P. Rule .
Gravitational Potential Energy: SCALAR.
Units: Joules.
Equation: PEg = m × g × h
Occasionally, PEg will be represented as Ug.
m = Mass of the object
g = Acceleration due to gravity
h = Vertical height from the horizontal zero line to the CENTER OF MASS OF THE OBJECT. 'h' is ALWAYS to the center of mass of the object - not to the very top. That is what 'height' means in this context. Everything else is irrelevant - h refers specifically to the height of the center of mass above the zero line.
Definition: The energy stored in an object due to that object's elevation. When an object is dropped from a height, the potential energy will become kinetic energy as the object falls.
h is the vertical displacement between an object's center of mass and the horizontal zero line, which is determined by the individual. Typically, the horizontal zero line will be placed at either the ground or the lowest position an object will be.
If you were to place the horizontal zero line above the object, h would be negative, and if the horizontal zero line were below the object, h would be positive. If the horizontal zero line were to be placed on the center of mass of the object, h (and thus PEg) would equal to zero.
Because m and g are always positive, it is h that determines the sign of the gravitational potential energy.
Units: Joules.
Equation: PEg = m × g × h
Occasionally, PEg will be represented as Ug.
m = Mass of the object
g = Acceleration due to gravity
h = Vertical height from the horizontal zero line to the CENTER OF MASS OF THE OBJECT. 'h' is ALWAYS to the center of mass of the object - not to the very top. That is what 'height' means in this context. Everything else is irrelevant - h refers specifically to the height of the center of mass above the zero line.
Definition: The energy stored in an object due to that object's elevation. When an object is dropped from a height, the potential energy will become kinetic energy as the object falls.
h is the vertical displacement between an object's center of mass and the horizontal zero line, which is determined by the individual. Typically, the horizontal zero line will be placed at either the ground or the lowest position an object will be.
If you were to place the horizontal zero line above the object, h would be negative, and if the horizontal zero line were below the object, h would be positive. If the horizontal zero line were to be placed on the center of mass of the object, h (and thus PEg) would equal to zero.
Because m and g are always positive, it is h that determines the sign of the gravitational potential energy.
#
P. Rule .
Elastic Potential Energy: SCALAR.
Units: Joules.
Equation: PEe = 1/2 × k × ∆x² (SAME EQUATION AS SPRING WORK)
Occasionally, PEe will be represented as Ue.
k = Spring constant (Newtons / meters, see Rule 81).
x = Displacement from equilibrium position (or rest position)
Definition: The energy stored in an object due to the temporary deformation of that object (e.g., elasticity before the elastic limit, the restoring force trying to bring it back to equilibrium). Most commonly, springs are the objects with elastic potential energy, though any object that is able to deform slightly and regain its initial shape has it as well. For example, a slighlty deflated ball will have elastic potential energy when it hits the ground and compresses slightly before reforming.
When a spring is elongated or compressed, the elastic potential energy can be converted into kinetic energy and gravitational potential energy.
Remember that the spring constant is directly proportional to the amount of force it takes to compress or elongate a spring. Because the spring constant is always positive, and because the displacement is squared, elastic potential energy is always positive.
Units: Joules.
Equation: PEe = 1/2 × k × ∆x² (SAME EQUATION AS SPRING WORK)
Occasionally, PEe will be represented as Ue.
k = Spring constant (Newtons / meters, see Rule 81).
x = Displacement from equilibrium position (or rest position)
Definition: The energy stored in an object due to the temporary deformation of that object (e.g., elasticity before the elastic limit, the restoring force trying to bring it back to equilibrium). Most commonly, springs are the objects with elastic potential energy, though any object that is able to deform slightly and regain its initial shape has it as well. For example, a slighlty deflated ball will have elastic potential energy when it hits the ground and compresses slightly before reforming.
When a spring is elongated or compressed, the elastic potential energy can be converted into kinetic energy and gravitational potential energy.
Remember that the spring constant is directly proportional to the amount of force it takes to compress or elongate a spring. Because the spring constant is always positive, and because the displacement is squared, elastic potential energy is always positive.
#
P. Rule .
The usage of the conservation of mechanical energy as a means of problem solving can come in unexpected ways. In the places where it is applicable, such as the movement of something through gravity (while ignoring air resistance), the formation of the full conservation equation (incorporating all of the component energies) can be useful:
MEi = MEf
KEi + PEgi + PEei = KEf + PEgf + PEef
1/2 × m × vi² + m × g × hi + 1/2 × k × xi² =
1/2 × m × vf² + m × g × hf + 1/2 × k × xf²
Whatever can be canceled out will simplify the equation, and it will be useful in a variety of circumstances.
MEi = MEf
KEi + PEgi + PEei = KEf + PEgf + PEef
1/2 × m × vi² + m × g × hi + 1/2 × k × xi² =
1/2 × m × vf² + m × g × hf + 1/2 × k × xf²
Whatever can be canceled out will simplify the equation, and it will be useful in a variety of circumstances.
#
P. Rule .
The signs of the individual works of the mechanical energies:
The work done by the force of kinetic friction is negative because it converts kinetic energy to heat and sound energy.
When Moving Upward, the work done by the force of gravity is negative because it converts kinetic energy into gravitational potential energy as the object moves against the gravitational force.
When Moving Downward, the work done by the force of gravity is positive because it converts gravitational potential energy into kinetic energy as the object moves in the direction of the gravitational force.
End of story.
The work done by the force of kinetic friction is negative because it converts kinetic energy to heat and sound energy.
When Moving Upward, the work done by the force of gravity is negative because it converts kinetic energy into gravitational potential energy as the object moves against the gravitational force.
When Moving Downward, the work done by the force of gravity is positive because it converts gravitational potential energy into kinetic energy as the object moves in the direction of the gravitational force.
End of story.
#
P. Rule .
When the work by the force applied to an object is equal to zero (WFa = 0), the work done by friction is equal to the change in mechanical energy.
Wf = ∆ME (when WFa = 0)
Ff × d × cos(θ) = MEf - MEi (when WFa = 0)
As you should see, the Conservation of Energy equation is a mere special case of this friction work equation, occuring when friction is equal to zero (because MEi can be moved to the other side).
Wf = ∆ME (when WFa = 0)
Ff × d × cos(θ) = MEf - MEi (when WFa = 0)
As you should see, the Conservation of Energy equation is a mere special case of this friction work equation, occuring when friction is equal to zero (because MEi can be moved to the other side).
#
P. Rule .
When a question tries to sneak past you that the 'mass' of an object is in Newtons (or another force-based unit), like stating that a "67 N ball" was dropped, the "Newtons" is simply referring to the weight of the ball, e.g. the force of gravity acting on the ball. Incorporating this into your calculations, you can calculate the mass by finding the net force in y-direction (or whichever direction the normal force is in, tilted axes or otherwise) and isolating m as needed.
VII.IV Conservative Forces.
#
P. Rule .
Conservative Force: A force in which the work done on an object is the same regardless of the path taken by the object. Conservative forces can return the kinetic energy back to the system after taking it away, conserving the mechanical energy - hence, conservative forces. It thus follows that nonconservative forces cannot have the conservation of energy laws applied.
Examples of conservative forces include the following:
Wconservative force = -∆U
The work done on the object by the force of gravity as the object goes down a distance h is always the same, no matter the angle of any incline the object may slide on.
With non-constant forces, the following equation can be used:
Fx = -(dU / dx)
Additionally, you can integrate both sides to get the following form:
$$\int_{x_i}^{x_f} F_x \, dx = -∆U$$
Both equations are applicable in different circumstances, being the same equation represented in different ways.
Examples of conservative forces include the following:
- Force of Gravity
- Spring Force
- Electromagnetic Force
- Magnetic Force
Wconservative force = -∆U
The work done on the object by the force of gravity as the object goes down a distance h is always the same, no matter the angle of any incline the object may slide on.
With non-constant forces, the following equation can be used:
Fx = -(dU / dx)
Additionally, you can integrate both sides to get the following form:
$$\int_{x_i}^{x_f} F_x \, dx = -∆U$$
Both equations are applicable in different circumstances, being the same equation represented in different ways.
# Nonconservative Force: A force in which the work done on an object depends on the path taken by the object. Examples include the following:
- Force of Friction
- Air Resistance
- Tension
# Properties of Conservative Forces:
All conservative forces have the following two equivalent properties:
- The work done by a conservative force on an object moving between any two points is independent of the path taken by the object.
- The work done by a conservative force on an object moving through any closed path equals zero (a closed path is a path where the initial and final points are the same location).
VII.V Energy Systems.
∆Esystem = Σ T
∆Esystem = Change in energy of the system
Σ T = Sum of the energy transferred into or out of the system
This equation states that the change in energy of the system equals the net energy transferred into or out of the system.
# Modes of Transferring Energy:
Energy can be transferred into or out of a system via:
- Mechanical Waves: Sound waves are energy being transferred from one system to another through a disturbance of a medium, whether that medium be air or even water.
- Work: A force applied can transfer energy to a system by doing work on the system.
- Heat: Heat is a way to transfer energy from one system to another via a difference in temperature.
- Electricity: Electrical current can transfer energy from one system to another, like how an electric motor can convert electric potential energy to kinetic energy in a rotating power drill.
- Radiation: Electromagnetic waves like visible light, ultraviolet light, radio waves, and microwaves can add energy to a system.
∆Esystem = WFa
Furthermore,
WFa = ∆ME + ∆Einternal
Change in internal energy of a system is caused by the work done by nonconservative forces like friction. E.g., the work done by nonconservative forces on a system converts mechanical energy into internal energy of the system.
When you rub your hands together, the kinetic energy of the motion of your hands is converted into internal energy in your hands, via work done by friction.
∆Einternal = -Wnonconservative
and, where there is no work performed by a force applied,
Wnonconservative = ∆ME
#
P. Rule .
Basic Principles:
1. ∆Esystem = Σ T []
2. ∆ME = ∆KE + ∆U []
Energy Transfer Calculations:
3. ∆Esystem = WFa []
4. WFa = ∆ME + ∆Einternal []
5. ∆Einternal = -Wnonconservative []
6. Wnonconservative = ∆ME [] (when WFa = 0, and is generally Wf)
Conservative Forces:
7. Wconservative force = -∆U []
8. Fconservative = -(dU / dx) []
9. $$\int_{x_i}^{x_f} F_{conservative} \, dx = -∆U$$ []
Basic Principles:
1. ∆Esystem = Σ T []
2. ∆ME = ∆KE + ∆U []
Energy Transfer Calculations:
3. ∆Esystem = WFa []
4. WFa = ∆ME + ∆Einternal []
5. ∆Einternal = -Wnonconservative []
6. Wnonconservative = ∆ME [] (when WFa = 0, and is generally Wf)
Conservative Forces:
7. Wconservative force = -∆U []
8. Fconservative = -(dU / dx) []
9. $$\int_{x_i}^{x_f} F_{conservative} \, dx = -∆U$$ []
#
P. Rule .
Identifying what forces are external and internal are very important to using the energy system equations: When the force is external, represent it using work, and if the force is internal, represent it using Potential Energy. See Rule 100 for how to determine whether a force is internal or external.
#
P. Rule .
Defining what forces acting on a system are external and internal is not as bad as you may think:
Suppose you have a system containing objects A and B, and a second system containing objects C and D. Any force object A exerts on B (or vice versa) is internal, because it is a force resulting from the interaction of two objects defined to be a part of the same system. If C or D exerted a force on A or B (or A or B exerted on C or D), the force is external, because the interaction involves objects that are and aren't in the system.
In the first case, quantities such as momentum and total energy will be conserved because the force was internal. This does not hold true in the second case, because the force was external.
Suppose you have a system containing objects A and B, and a second system containing objects C and D. Any force object A exerts on B (or vice versa) is internal, because it is a force resulting from the interaction of two objects defined to be a part of the same system. If C or D exerted a force on A or B (or A or B exerted on C or D), the force is external, because the interaction involves objects that are and aren't in the system.
In the first case, quantities such as momentum and total energy will be conserved because the force was internal. This does not hold true in the second case, because the force was external.
#
P. Rule .
Gravitational energy only exists when you have at least two objects in your system: When the Earth is not part of the system, and there is only one object in the system, then the system cannot have gravitational potential energy. Thus, the work done by the force of gravity will be an external force when the system is not declared to include the Earth, or whatever planet the event is occurring on.
Newton's third law force pairs are always internal forces. When a system includes an object and the Earth, the force of gravity of the object acting on the block, and the force of gravity of the object acting on the earth, are equal in magnitude and opposite in direction. This does NOT mean that the force normal and force of gravity go together; Force Normal is always an external force.
Newton's third law force pairs are always internal forces. When a system includes an object and the Earth, the force of gravity of the object acting on the block, and the force of gravity of the object acting on the earth, are equal in magnitude and opposite in direction. This does NOT mean that the force normal and force of gravity go together; Force Normal is always an external force.
#
P. Rule .
Know that instead of just summing the forces in one direction at a time, you can sum all of them at once in unit vector form, where you assign each of the forces î, -î, ĵ, or -ĵ depending on their direction. If the force is not squarely in a unit vector direction (e.g., it is at an angle not cleanly divisible by 90), then just incorporate both î & ĵ into one force. Know that you should also write acceleration in it unit vector form if you can. Once you have an equation in this unit vector form, you can once again isolate the x and y direction vectors to solve for any missing variables.
VII.VI Energy Wells.
There are three types of equilibrium an object can be in as it remains in a gravitational field. These three types arise from the different ways in which the object’s potential energy can change when the object undergoes a displacement. For each direction, if the change in potential energy equals zero, the object is in translational equilibrium in that direction.
- Neutral Equilibrium: The potential energy is constant. A displacement in any direction will not change the object's potential energy, and when the object is displaced, it will not experience any force that will increase its displacement nor bring it back to its original position.
Example: A ball rolling back and forth on a level surface will be in neutral equilibrium because its gravitational potential energy will remain constant regardless of its position.
The graph of the gravitational potential energy of the ball (with respect to position) will be a horizontal line because the g.p.e. is constant. - Stable Equilibrium: The potential energy is at a minimum. Displacing the object to either side will raise its potential energy, resulting in a (gravitational) force that moves the object back towards its original position. Since displacing the object will raise its potential energy, any force that would displace the object from its original position must do work on it to do so.
Example: A tiltable water bottle will be in stable equilibrium because its gravitational potential energy increases as its position moves away from the equilibrium position. As the water bottle is tilted, the center of mass will go up as the position goes away from equilibrium. The water bottle will naturally return back to the equilibrium position when it loses gravitational potential energy.
The graph will look akin to an energy well, with the equilibrium position in the center of the well. - Unstable Equilibrium: The potential energy is at a maximum. Displacing the object to either side will lower its potential energy, resulting in a (gravitational) force moving the object further from its original position. Since displacing the object lowers its potential energy, gravity does the work necessary to displace the object from its original position.
Example: Something easily toppleable, like a pen, will be in an unstable equilibrium because its gravitational potential energy decreases as it moves away from the equilibrium position, because the center of mass of the pen goes down as the pen gets displaced from the equilibrium. The pen will naturally move away from the equilibrium position when it loses gravitational potential energy.
The graph will look akin to an energy 'mountain' of sorts, with the equilibrium position at the peak, making it very easy for the object to go from potential energy to kinetic energy.
# Potential Energy Curves: Acknowledge Equation 8 of the Energy Transfer Equation Cheatsheet (see Rule 98), which is the derivation of Equation 9.
If U(x) is given on a graph, then at any value of x, the force F(x) is the negative of the slope of the curve there and the kinetic energy of the particle is given by KE = Emec - U(x), where Emec c is the mechanical energy of the system.
A turning point is a point x at which the particle reverses its motion (there, K = 0). The particle is in equilibrium at points where the slope of the U(x) curve is zero (there, F(x) = 0).