These are my complete notes for Derivatives in Differential Calculus.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Derivatives (Differential Calculus)
?. Derivative.
# Rule 130. A secant line is a line that intersects the line at two places. The slope of the secant line is the average rate of change between the two points.
# Rule 131. A tangent line is a line that intersects a curve at exactly one point. The slope of the tangent line is the instantaneous rate of change at a point.
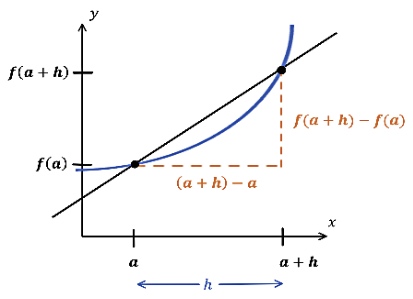
# Difference Quotient: $$\frac{f(x + h) - f(x)}{h}$$ The "Difference Quotient", given above, represents the secant line of a curve from the point (a, f(a)) to (a+h, f(a+h)), which is also the average rate of change from x=a to x=a+h:
# Normal Line: The line normal to a curve is the line perpendicular to the tangent at that point.
# Rule 132. When the limit exists, it's called the derivative of f at a, or any point. The derivative is f'(x) = $$\lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$ provided the limit exists. "Differentiate" means to determine the Derivative.
# Verbal Descriptions of Calculus Notation:
# Rule 133. Graphing the derivative without knowledge of the formulas for dy/dx nor the parent function, is wack:
First, get the slope between two points on the original f(x) and find the slope. As x increases, a decreasing f(x) value indicates a negative slope, while an increasing f(x) value indicates a positive slope. Find an x-value in the middle of the two points and use it as the x-value. Use the slope as the y-value and plug into the new graph, and repeat. Fo a graph with "pointy points", known as corners, they are undefined in the derivative graph (the f'(x)), as they do not have local linearity (see [[[).
# Rule 134. When a fraction has a square root, standard procedure is to multiply it by a conjugate, especially if the square root is on the denominator.
# Rule 135. For the alternate definition of the derivative, you always want to do all the algebra first before substituting for a at the end. Then, you can do a.
# Rule 136. Function f(x) is differentiable on a closed interval [a, b] if it has a derivative at every interior point of the interval, and if the limits below exist at the endpoints.
$$\lim_{h \to 0^+} \frac{f(a + h) - f(a)}{h}$$ is the right-hand derivative, and
$$\lim_{h \to 0^-} \frac{f(b + h) - f(b)}{h}$$ is the left-hand derivative.
# Rule 137. The left hand derivative can be found by using the regular f(x), while the right hand derivative is found by using the equation of the f'(x) derivative found from the left hand derivative. If the two derivatives are equal to each other, then the derivative in totality is real.
