These are my complete notes for Particle Motion in Differential Calculus.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Particle Motion (Differential Calculus)
?. Particle Motion.
# Rule 146. If s(t) represents the position of an object, then the velocity of the object is given by v(t) = s'(t). If v'(t) represents the velocity of an object, then the object's speed is given by the absolute value of velocity. speed = |v(t)| = |s'(t)|.
# Acceleration: If v(t) represents the velocity of an object, then the acceleration of the object is given by a(t) = v'(t) = s''(t). This represents the rate at which the rate of change is changing (see Rule 147).
# Rule 147. Velocity is the speed in relation to something, so a ball can have negative and positive velocity as it is thrown in the air. Speed is just how fast it's going, and nothing can ever go negative speed.
Acceleration is the derivative of velocity, is the derivative of speed. Acceleration is positive wherever the line of the velocity graph is increasing and negative when decreasing.
# Fundamental Particle Motion Terms:
Displacement: S(tf) - S(ti), in effect (PositionFinal - PositionInitial)
Average Velocity: (∆S / ∆t)
Instantaneous Velocity: (ds/dt), v(t) = s'(t)
# Rule 148. Displacement is the distance between where you started from and where you ended up.
Total distance is how much distance you covered. For example, the displacement can be zero because you can end up exactly where you started.
# Application of Calculus: Cost Modeling:
In manufacturing, the cost of production c(x) represents the cost of producing x number of units. The marginal cost is the rate of change, or "the cost to produce one more item". Marginal cost is the derivative of cost: c'(x).
Revenue, r(x) is the total amount of money collected for the sales of a product. Marginal Reveue is the total amount collected from selling one more unit. r'(x) = Marginal Revenue.
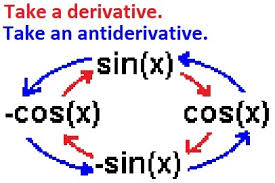
# Sine-Cosine Derivative Loop:
# Rule 149. To find when a particle is moving forward or backward, make a number line for the x's of the velocity graph and find when it is negative or positive: positive is forward, negative is backward.
For where the particle is speeding up or slowing down, if the particle has v(t) > 0 & a(t) < 0, or v(t) < 0 & a(t) > 0 (e.g., the signs do not match between the velocity and acceleration), then the particle is slowing down.
If the particle has v(t) < 0 & a(t) < 0 or v(t) > 0 & a(t) > 0 (matching signs between velocity and acceleration) then the particle is speeding up.
