This is the first part of my complete notes for Classical Mechanics, covering topics of Kinematics such as Velocity, Speed, Acceleration, Free Fall, Projectile Motion, Range, and more. Due to the large scale of this topic, I have had to split even the complete notes into multiple parts.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Classical Mechanics, Part 1: Kinematics
Table Of Contents
I. Velocity, Speed, Acceleration.
I.I The Bare Minimum.
What you should retain as knowledge for your life, regardless of whether you waste it or if you pursue Physics, are these Bare Minimum fundamentals, which you must carry with you in all future pursuits.
# Units & Dimensions:
Physics is based on the measurement of physical quantities. Dimensions are the individual types of physical quantities, like length, mass, and time, while Units are the explicit means by which they are measured, like meters, pounds, and kilograms.
There are several different systems of measurement which measure the same types of dimensions, the two biggest systems being the Metric System (a.k.a. the S.I.) and the Imperial System, all others being scams. For example, length is measured in 'meters' in the metric system, while the imperial unit for length is 'feet'.
A simple chart of the popular unit types and their respective base dimensions.
In Physics, the metric system (S.I. units) is the industry standard, and even then, units are converted using conversion factors (see "Dimensional Analysis") into their base dimensions.
#
P. Rule .
When doing a problem, ALWAYS convert all given units into the base S.I. Units unless told otherwise - see the "Units & Dimensions" blue section for these base units. There is a purpose for this beyond what custom has strictly divided - several units are defined in terms of the base units (like Joules in Section VII).
Generally, this will be your first step in any Physics problem involving non-base units, unless the question expressly states that the answer must be given in terms of non-base units. Either way, you need to standardize all dimensions in your problem into the same unit, like having every weight value in kilograms.
Generally, this will be your first step in any Physics problem involving non-base units, unless the question expressly states that the answer must be given in terms of non-base units. Either way, you need to standardize all dimensions in your problem into the same unit, like having every weight value in kilograms.
# Dimensional Analysis:
Being comfortable in performing Dimensional Analysis (conversion from one unit of measurement to another) is critical to all of Physics; it is the underlying prerequisite concept which all problems assume knowledge of.
Dimensional Analysis is conducted using conversion factors, which are just ratios of units that, when multiplied to the original unit, allow you to change the unit without changing the quantity. They allow you to cancel out the original unit, leaving you with the desired one. For example, in converting from hours to seconds,
(2 hours) x (60 min/1 hour) x (60 sec/1 min)
has (60 min/1 hour) and (60 sec/1 min) as the conversion factors, converting from hours to minutes and then minutes to seconds, respectively.
The conversion factor is the fraction being multiplied regardless of the coefficient of the original unit, as shown in how two minutes, 40 minutes, and 542 minutes will all have the same conversion factor when converting into seconds.
Conversion factors, thus, include the desired final unit (or atleast a unit closer to the unit you are trying to get to) in the equivalent ratio with the previous unit, either the one you started with or the previous unit in the conversion factor sequence. Inherently, every conversion factor must equal to one, as the top and bottom are the same value, just expressed in different ways.
#
P. Rule .
When converting one exponentiated unit (², ³, etc.) into another using dimensional analysis, put the exponent on the outside of the parenthesis of the conversion factor (see "Dimensional Analysis" blue section), applying the exponent to the top and bottom in order to allow units to cancel out:
12 mm² → m² = 12 mm² × ((1 m) / (1000 mm))²
= 12 mm² × ((1 m)² / (1000 mm)²)
= 12 mm² × ((1 m²) / (1000000 mm²))
= (1.2 x 10⁻⁵) m²
12 mm² → m² = 12 mm² × ((1 m) / (1000 mm))²
= 12 mm² × ((1 m)² / (1000 mm)²)
= 12 mm² × ((1 m²) / (1000000 mm²))
= (1.2 x 10⁻⁵) m²
# Density:
The density d of a material (the amount of mass in a given space) is the mass per unit volume:
d = (m / V)
Much of the time, an object's density will be described in the base metric units (see the "Units & Dimensions" blue section). As such, densities tend to be given with the units kilograms per cubic meter (kg/m³).
Other metric units will occasionally be used in defining a density: The density of water, for example, is 1.00 gram per cm³. In a problem, unless stated otherwise, these values should be converted into base units to establish uniformity (as stated in Rule 1).
# Dimensional Analysis Comprehension Problem:
Here is an example problem that should not pose too much of an issue to any beginning physicist well-versed in dimensional analysis:
Iron has a density of 7.87 g/cm³, and the mass of an iron atom is 9.27 × 10⁻²⁶ kg. If the atoms are spherical and tightly packed,
(a) what is the volume of an iron atom and
(b) what is the distance between the centers of adjacent atoms?
Answer(s):
a) 1.18 × 10⁻²⁹ m³
b) 2.82 × 10⁻¹⁰ meters
Explanation:
The first step of any Physics problem, as noted in Rule 1, is to convert all measurements into the same units. As the question gives no preference as to what units the answer should be presented, base units should be presumed, and so we will first convert the grams to kilograms and the cubic centimeters to cubic meters:
dI = (7.87 g/cm³) × (1 kg / 1000 g) × (100 cm / 1 hr)³
dI = 7.87 × 10³ kg/m³
Now, the actual problem-solving part of the problem can commence. In order to actually find the volume of the iron atom for part a), one must remember the density equation (described in the "Density" blue section): d = (m / V). Thus, the first and only step for part a) would be to isolate the volume, since the density and mass is already known.
V = (m / dI)
V = (9.27 × 10⁻²⁶ kg) / (7.87 × 10³ kg/m³)
This gives us a result of 1.18 × 10⁻²⁹ m³ for the volume of an iron atom.
Next, for part b), we need to find the distance between the centers of adjacent atoms. Using critical thinking, we can determine that this distance is in fact the diameter of the atom, which we can reverse engineer by isolating the radius from the volume equation of a sphere:
Volume of sphere = (4/3) × π × r³.
r = ∛(3V / 4π)
Plugging in the known volume from answer a), we find that the radius is equal 1.41 × 10⁻¹⁰ meters. Since we are looking for the diameter, we multiply this distance by two and get 2.82 × 10⁻¹⁰ meters.
#
P. Rule .
SIGNIFICANT FIGURES:
'Significant Figures', also known as the Digits of Precision, are the digits within a number that indicate how precise a measurement can be ascertained to be. If a recipe calls for has 1 teaspoon of sugar, you could probably eyeball it, but if it calls for 1.000000 teaspoons of sugar, that's a lot more precise; you'd probably need a laboratory-level scale to get that exact of a measurement.
With significant figures, often abbreviated to sig. fig.'s, perceived preciseness only translates to genunine preciseness half of the time. Below is a simple set of guidelines to follow when determining how many sig. fig.'s are in any number:
#1) All Non-zero digits are significant.
#2) Zeros between significant digits are significant.
#3) Zeros to the left of nonzero digits are not significant.
#4) Zeros at the end of a number are significant only if there is a decimal point present.
The given values, 1 and 1.000000 have different numbers of sig. fig.'s, 1 and 7 respectively, and thus have differing levels of preciseness. However, note that under these immutable guidelines, 0.00001 and 1 have the same number of sig. fig.'s, because zeroes to the left of nonzero digits are not significant (#3).
In Physics, it is convention to use sig. fig.'s in all numerical answers, with the number of significant figures in the answer being equal to the least number of figures in any of the numerical values given in the question. However, never use sig. fig.'s to alter the values used in your actual calculations; only use them to alter your final answer, and even thereafter, if you need to use that answer in another part of the problem, use the un-sigfig'd version to perform your calculations.
Examples:
0.000001 has ONE sig. fig., as a result of guideline 3.
1200 with 3 significant figures: 1.20 x 10³
0.002 with 3 significant figures: 2.00 x 10⁻³
'Significant Figures', also known as the Digits of Precision, are the digits within a number that indicate how precise a measurement can be ascertained to be. If a recipe calls for has 1 teaspoon of sugar, you could probably eyeball it, but if it calls for 1.000000 teaspoons of sugar, that's a lot more precise; you'd probably need a laboratory-level scale to get that exact of a measurement.
With significant figures, often abbreviated to sig. fig.'s, perceived preciseness only translates to genunine preciseness half of the time. Below is a simple set of guidelines to follow when determining how many sig. fig.'s are in any number:
#1) All Non-zero digits are significant.
#2) Zeros between significant digits are significant.
#3) Zeros to the left of nonzero digits are not significant.
#4) Zeros at the end of a number are significant only if there is a decimal point present.
The given values, 1 and 1.000000 have different numbers of sig. fig.'s, 1 and 7 respectively, and thus have differing levels of preciseness. However, note that under these immutable guidelines, 0.00001 and 1 have the same number of sig. fig.'s, because zeroes to the left of nonzero digits are not significant (#3).
In Physics, it is convention to use sig. fig.'s in all numerical answers, with the number of significant figures in the answer being equal to the least number of figures in any of the numerical values given in the question. However, never use sig. fig.'s to alter the values used in your actual calculations; only use them to alter your final answer, and even thereafter, if you need to use that answer in another part of the problem, use the un-sigfig'd version to perform your calculations.
Examples:
0.000001 has ONE sig. fig., as a result of guideline 3.
1200 with 3 significant figures: 1.20 x 10³
0.002 with 3 significant figures: 2.00 x 10⁻³
#
P. Rule .
THE ARCANE ROUNDING RULE:
When rounding, if the number ends in a perfect 5, round to the even number.
Examples:
275 with 2 Significant figures: 280
1030 x 5.1 = 5300
When rounding, if the number ends in a perfect 5, round to the even number.
Examples:
275 with 2 Significant figures: 280
1030 x 5.1 = 5300
# Atomic Mass Units:
An additional unit of measurement (derived from kg) specific to atoms (and only occasionally relevant to elementary Physics) is the Atomic Mass Unit, defined as the "atomic mass" of each element in relation to that of Carbon-12. Specifically, Carbon-12 is defined as having 12 amu, and other atoms are calculated in relation to how much mass they have in relation to Carbon-12.
For those familiar with stoichiometry, the amu can be converted to moles easily.
For Mechanics and Electromagnetism, idealized particles or electrons/protons are generally used instead of atoms of a specific element, so for now, only a more peripheral understanding of amu is needed. This relative disregard lasts until higher level Nuclear Physics, which has more of an emphasis on that sort of thing.
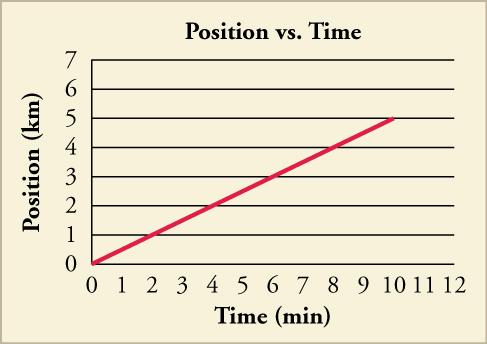
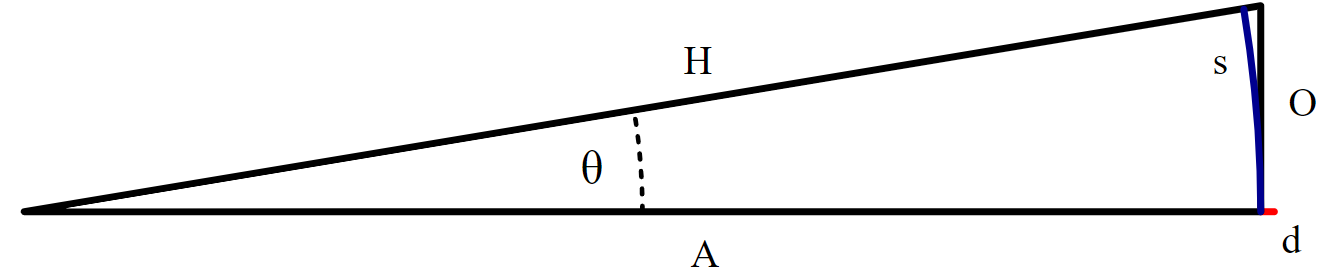
# Vertical Scaling:
When you have a problem that makes reference to the vertical or horizontal scaling of a graph (such as the one shown below), the "vertical scaling" is just referring to what the given height value is as each y-value is multiplied by a constant, creating a ratio between the new and original scales.
The old scale will almost always be a scaling of 1:1 (i.e. the normal graph), and the new scale will have a scaling ratio determined by the vertical scaling and its positioning on the graph.
For example, the new scale as depicted in the graph below has a ratio of 2:1 with the old scale, demonstrated by how vs is eight units upward, meaning each unit is two. The exact same process can be applied to the x-axis, resulting in Horizontal Scaling.
A Physics problem involving vertical scaling. It is done through integration, if you must know.
#
P. Rule .
Coordinate/Direction Types:
There are three types of directions/coordinates that are critical to one's directional understanding in Physics and life in general: Cartesian, Relative, and Cardinal.
Cartesian Coordinates: (x, y).
A graph with random cartesian coordinates. Courtesy of GIS.
Relative Coordinates: (Left, Right).
A graph with relative directions like right and back superimposed over it.
Cardinal Direction: (North, South)
A compass, with each of the cardinal directions labeled.
There are three types of directions/coordinates that are critical to one's directional understanding in Physics and life in general: Cartesian, Relative, and Cardinal.
Cartesian Coordinates: (x, y).
A graph with random cartesian coordinates. Courtesy of GIS.
Relative Coordinates: (Left, Right).
A graph with relative directions like right and back superimposed over it.
Cardinal Direction: (North, South)
A compass, with each of the cardinal directions labeled.
I.II Accuracy & Uncertainty.
# Precision: How close the observed/measured values are to one another.
# Relative Error: A measure of accuracy.
Er = ((O - A) / A) × 100
Er = Relative Error. Measures the accuracy of the observed value in relation to the accepted value. Explicitly, it is a percentage representation of the difference between the accepted value and the observed value.
O = Observed Value. If it perfectly matches the accepted value, then there is no error and the Er is equal to 0.
A = Accepted Value.
#
P. Rule .
When finding the accuracy of a selection of observed values, know that you must take an average, either at the beginning or end of your calculations.
For the beginning, you can just take the average of all the observed values immediately, and then use that value as your Observed Value (O) variable in the Relative Error equation (see the "Relative Error" blue section) to find the accuracy.
For the end, you can take the average of all the relative errors, each of which is calculated using one of the observed values. It should give you the same answer as averaging the observed values in the beginning.
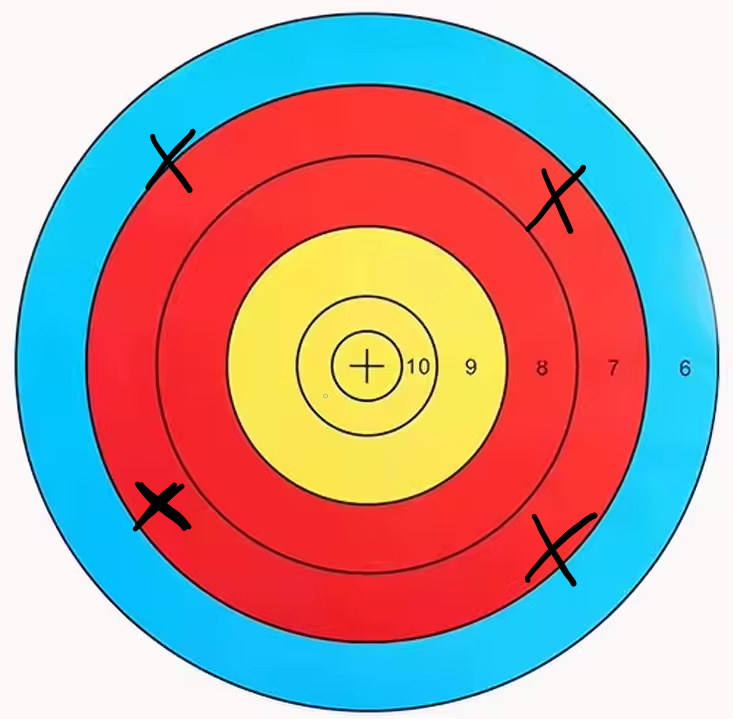
Either way, as a result of taking an average of the results, a bullseye that looks like this:
A target with four hits shown medium-distance from the center, forming a high accuracy average.
would be considered to have high accuracy, as they are all equidistant from the middle and thus have their center directly upon it.
For the beginning, you can just take the average of all the observed values immediately, and then use that value as your Observed Value (O) variable in the Relative Error equation (see the "Relative Error" blue section) to find the accuracy.
For the end, you can take the average of all the relative errors, each of which is calculated using one of the observed values. It should give you the same answer as averaging the observed values in the beginning.
Either way, as a result of taking an average of the results, a bullseye that looks like this:
A target with four hits shown medium-distance from the center, forming a high accuracy average.
would be considered to have high accuracy, as they are all equidistant from the middle and thus have their center directly upon it.
#
P. Rule .
If there is only one known measured value (that thus cannot be compared to any other measurements), precision cannot be determined.
I.III Uncertainty.
Whenever you are performing a measurement (not a calculation, a MEASUREMENT) in a serious Physics environment, you always need to have an estimated uncertainty to make your work falsifiable.
# Percent Uncertainty: A measure of precision.
Equation:
P = (E / O) × 100
P = The Percent Uncertainty, a measure of precision. The closer the value to 0%, the more precise the observed value is.
E = The Estimated Uncertainty, a.k.a. the number immediately following the ±.
O = The Observed Value.
Definition: The ratio between the estimated uncertainty and the measured value, made into a percentage.
The given equation for percent uncertainty is remarkably similar to the relative error equation, the difference lying in how percent uncertainty only conveys the possible error (uncertainty) in the observed value as a proportion of the observed value itself, while relative error conveys the percentage of the difference between the observed value and the accepted value as a proportion of the accepted value.
Percent uncertainty is a measure of precision through how the answer shows how close the observed and accepted values are to one another (the closer the answer is to 0%, the more precise the observed value is).
For example, with the measurement 8.8 ± 0.1 m, the percent uncertainty would be ((0.1) / (88)) × 100% ≈ 1%.
#
P. Rule .
If a questions asks for the approximate uncertainty (see "Estimated Uncertainty" definition) of something, but gives no hints on how to find it, assume ±1 unit at the lowest digit of precision (under sig. fig. rules given in Rule 3). Additionally, any and all scientific notation on the original value must be extended to all estimated uncertainty assumptions. For example, if the question gives a value of 4.19 × 10³ m, then an estimated uncertainty of 0.01 × 10³ should be presumed.
However: Know that, in practically all cases, this ±1 of whatever unit is not the answer they are looking for. The question will oftentimes phrase the question cleverly, asking for the approximate uncertainty of a shape as a whole but only giving the radius as the given value, causing the ±1 assumption to only be in reference to the radius and requiring additional work to find the approximate uncertainty of the shape.
The question will likely want you to plug in the positive and negative versions of the assumed estimated uncertainty (individually added onto the main value to create two separate values) into another equation in order to find a final approximate uncertainty. This process is detailed in Rule 9, which uses a circle as its example equation.
However: Know that, in practically all cases, this ±1 of whatever unit is not the answer they are looking for. The question will oftentimes phrase the question cleverly, asking for the approximate uncertainty of a shape as a whole but only giving the radius as the given value, causing the ±1 assumption to only be in reference to the radius and requiring additional work to find the approximate uncertainty of the shape.
The question will likely want you to plug in the positive and negative versions of the assumed estimated uncertainty (individually added onto the main value to create two separate values) into another equation in order to find a final approximate uncertainty. This process is detailed in Rule 9, which uses a circle as its example equation.
#
P. Rule .
When you want to find the approximate uncertainty of a 2D shape, use the shape's ideal area formula. If you want to find the approximate uncertainty of a 3D shape, use its volume formula.
For example, if you want to find the approximate uncertainty of a circle given the radius, use πr² as your area formula.
As a general problem example, you are asked to find the approximate uncertainty of a circle with the radius r = 3.8 × 10⁴ m. Of course, A = 4.5 × 10⁹ m². From there, since no percent uncertainty is given, then (as stipulated in Rule 8) you would assume an approximate uncertainty of 0.1 of the original units, ± 0.1 × 10⁴ m. This finds the approximate uncertainty in relation to the radius, but now what must be found is the approximate uncertainty of the circle itself.
From there, you would plug in two values for r into the area equation: the given radius with the approximate uncertainty added (Amax), and with the approximate uncertainty subtracted (Amin). This will produce two distinct areas: Amax = 4.8 × 10⁹. Amin = 4.3 × 10⁹.
At this point, follow this equation: ½(Amax - Amin). Find the difference between the areas, and then divide by 2. This first finds the complete range of the approximate uncertainty of the circle, and then halves it to produce the value that can be placed in front of the ± symbol. This results in a final answer of (4.5 ± 0.24) × 10⁹ m², with ± 0.24 × 10⁹ m² as the circle's approximate uncertainty.
You may wonder whether it would be possible to obtain the final approximate uncertainty by simply finding the difference between Amax and the area using the base radius, circumventing the entire process of finding the difference between both approximate uncertainties and then dividing by two. Sadly, such an idea is too good to be true. This is not feasible as a result of any and all exponential functions in the area/volume equation. If the equation is linear, then it can be done, but it is a better rule of thumb to just always do the process of ½(Amax - Amin) to avoid making unnecesary mistakes.
For example, if you want to find the approximate uncertainty of a circle given the radius, use πr² as your area formula.
As a general problem example, you are asked to find the approximate uncertainty of a circle with the radius r = 3.8 × 10⁴ m. Of course, A = 4.5 × 10⁹ m². From there, since no percent uncertainty is given, then (as stipulated in Rule 8) you would assume an approximate uncertainty of 0.1 of the original units, ± 0.1 × 10⁴ m. This finds the approximate uncertainty in relation to the radius, but now what must be found is the approximate uncertainty of the circle itself.
From there, you would plug in two values for r into the area equation: the given radius with the approximate uncertainty added (Amax), and with the approximate uncertainty subtracted (Amin). This will produce two distinct areas: Amax = 4.8 × 10⁹. Amin = 4.3 × 10⁹.
At this point, follow this equation: ½(Amax - Amin). Find the difference between the areas, and then divide by 2. This first finds the complete range of the approximate uncertainty of the circle, and then halves it to produce the value that can be placed in front of the ± symbol. This results in a final answer of (4.5 ± 0.24) × 10⁹ m², with ± 0.24 × 10⁹ m² as the circle's approximate uncertainty.
You may wonder whether it would be possible to obtain the final approximate uncertainty by simply finding the difference between Amax and the area using the base radius, circumventing the entire process of finding the difference between both approximate uncertainties and then dividing by two. Sadly, such an idea is too good to be true. This is not feasible as a result of any and all exponential functions in the area/volume equation. If the equation is linear, then it can be done, but it is a better rule of thumb to just always do the process of ½(Amax - Amin) to avoid making unnecesary mistakes.
I.IV Displacement and Velocity, Speed, Acceleration.
# Displacement: The change in position of an object. Mathematically, this means the straight-line distance between the initial and final points, also including direction*. ∆x ("delta-x") is the symbol for displacement and change in position, defined as positionfinal - positioninitial.
Although referred to as ∆x, displacement can have both x and y distance, as ∆x is in reference to position and not just the x-value. This can be somewhat confusing at times, and to add to the confusion, some problems will use ∆x to refer specifically to movement in the x-direction (such as U.A.M. problems, which will be discussed in Subsection I.V), while others use it to refer to positional change as a whole. It is up to you to use your proper judgment to discern the context as to what the ∆x of a problem represents.
*Displacement is a VECTOR (see Section III, on vectors), meaning that it incorporates direction in addition to magnitude. Thus, displacement can be negative or positive, depending on the direction traveled from the initial position. Vectors, as shown below, are depicted with an arrow above the variable.
Unit Vectors are a simplification of x and y positions into their respective directions, detailed in Rule 20. The equation for displacement (using d for displacement) in terms of unit vectors is d = (x₂ - x₁)î + (y₂ - y₁)ĵ
This equation describes displacement in terms of its component vectors on the x-axis and y-axis (see Rule 18). These component vectors indicate the direction and magnitude of the displacement.
In order to find the magnitude of the displacement in the graphical sense, where you have two dots on a graph (the start and end points) and you need to find the straight-line distance between them, you must first find the component vectors in the x and y directions. This will allow you to find the hypotenuse of the right triangle formed by the x and y component vectors (see Rule 18 & Rule 19):
|d| = √((x₂ - x₁)² + (y₂ - y₁)²)
Use this equation when prompted to find the magnitude of the displacement - the direction can be determined by the component vectors themselves; see Rule 20.
#
P. Rule .
NOTE THAT THE DISPLACEMENT EQUATION IS NOT NECESSARY IF THE OBJECT IS ONLY MOVING ALONG A SINGLE AXIS. If the position is only moving along one axis, then you only need to subtract yfinal by yinitial, xfinal by xinitial, or zfinal by zinitial to find displacement.
If not one-dimensional, then the displacement will have to be fully acknowledged as a vector, making use of the given equations above. If the movement is in 2D, then you want to use the magnitude equation as stated, and if it is in 3D, then you should just add + (z₂ - z₁)² is using the magnitude equation or + (z₂ - z₁)k̂ if using the unit vector equation. Useful proof.
If not one-dimensional, then the displacement will have to be fully acknowledged as a vector, making use of the given equations above. If the movement is in 2D, then you want to use the magnitude equation as stated, and if it is in 3D, then you should just add + (z₂ - z₁)² is using the magnitude equation or + (z₂ - z₁)k̂ if using the unit vector equation. Useful proof.
# Total Distance: The cumulative distance traveled between the starting and ending points of the particle.
The total distance traveled will always be greater or equal to the magnitude of displacement, as a result of the fact that total distance accounts for the path taken by the object, and not just the difference between the initial and final positions.
# Velocity: The rate of change of an object's position, utilizing displacement. Velocity has both magnitude and direction (thus making it a vector, described more in Section III), as shown in the below equalities:
Velocity = V
= (∆x / ∆t)
= (xF - xi) / (tF - ti)
= (Change in Position) / (Change in Time)
# Instantaneous Velocity: The velocity at a specific point in time. The Velocityfinal and Velocityinitial from the U.A.M. equations (see section I.V) are instantaneous velocities because they represent the object's velocity at a specific point in time.
# Average Velocity: The velocity over a time period. The velocity definition, change in position over change in time, is an average velocity itself.
#
P. Rule .
An average velocity written as V(5-10 sec) is just (x10 - x5) / (t10 - t5). This style of writing, although can be misinterpreted as meaning V-5 sec, specifies an interval on the graph to find the velocity of.
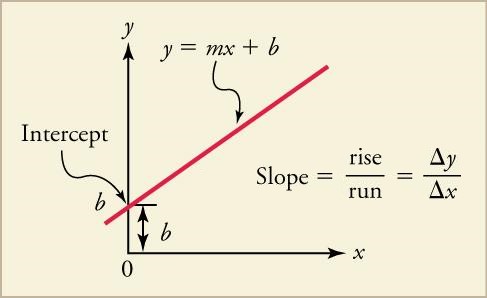
# Slope: The rate of change of a line in a graph, visually identifiable as the steepness of the line. Because the slope is merely a characteristic of a line (its steepness) rather than an actual quantity with direction, it is not a vector and is merely a numerical value (a "scalar", as will described in Subsection III.I).
The steepness of the line at a particular point is the instantaneous slope, better known as the instantaneous velocity (if the line is from the position graph). Below are the equalities for average slope:
Slope = m
= (rise / run)
= (∆y / ∆x)
= (yF - yi) / (xF - xi)
= (Change in Position / Change in Time).
In much the same way as Average Rate of Change (as detailed in the "Average Rate of Change (Contextualized)" blue section), the slope of a "position as a function of the time" graph is the velocity, while the slope of a "velocity vs. time" graph is acceleration. See "The Truth About Velocity & Displacement" for further elaboration.
# Acceleration: The rate of change of velocity. Since velocity is in meters over seconds, acceleration is in in meters per seconds per second, or m/s². Acceleration, as a function of velocity, has both magnitude and direction.
Acceleration = a
= (∆v / ∆t)
= (vF - vi) / (tF - ti)
= (Change in Velocity) / (Change in Time)
Imagine a ball is rolling on an incline, and assume it has a constant acceleration of 2 meters per second squared. What this means is that with each passing second, the velocity will increase by 2 m/s. The ball will start at 0 m/s in velocity and, after 1 second, will get to 2 m/s.
Since this example uses a constant acceleration, finding the position of the ball at each of those times is as simple as using the second U.A.M. equation (detailed in Subsection I.V).
# Average Rate of Change (Contextualized):
When used in different contexts, the 'Average Rate of Change' (A.R.O.C.) can mean different things:
When used in terms of f(x):
A.R.O.C. = Average Velocity = (Displacement / Change in Time).
When used in terms of f'(x):
A.R.O.C. = Average Acceleration = (Change in Velocity / Change in Time).
# Speed: The magnitude-only version of velocity, utilizing the total distance traveled by an object instead of displacement.
Because Velocity accounts for displacement, but speed only for distance traveled, they will only share the same magnitude when the object is moving in a straight line. Velocity specifically uses straight-line distance, so even if the line is curved, the start and end points would still be the only things used to calculate velocity. However, the speed of that curve uses the length of the entire line, all of the distance traveled between point a and point b.
Speed = v
= (total distance) / (time).
As shown above, speed generally uses the same symbol as velocity. The specific symbol being used in a given question is always discernable by the context of the problem.
#
P. Rule .
The object is speeding up whenever velocity and acceleration are in the same direction (e.g. they are the same sign), while it is slowing down whenever velocity and acceleration are in opposite directions/signs.
# The Truth About Velocity & Displacement:
In your reading of Velocity and Slope, you have no doubt encountered these three truths:
Velocity = ∆x / ∆t (Displacement / Change in Time)
Slope = ∆y / ∆x (Change in Y / Change in X)
Velocity = Slope
The '∆x' of the slope equation is not referring to displacement, but rather the change in the x-position. As stated in the displacement definition, ∆x will not uniformly represent displacement in every problem you come across, and even in the given equality there are two different usages of ∆x: displacement and change in x-position. In Physics, you must always use your best judgment to ascertain what the ∆x of a problem represents.
Here are the two equations shown as equivalent:
∆x1 ∆y
━━ = ━━
∆t ∆x2
In addition to knowing that the two equations are equivalent, we know that the ∆x1 of displacement and ∆x2 of slope are not the same, as they refer to displacement and change in x-position, respectively. if we were to cancel out the ∆x of the right side by multiplying it by both sides, we would find that ∆x² / ∆t is equal to ∆y, which is total nonsense.
The key to understanding how the equality is true (and how the ∆x is referring to two things simultaneously) is to realize that both equations are stating the same ratio, just in terms of different graphs.
A graph of the slope of a line in terms of y and x. Courtesy of Texas Gateway.
A graph of position versus time, identical to the graph above. Courtesy of Texas Gateway.
The equations are both output/input, and they both produce velocity when the slope is calculated between any two points. If the graphs were from the standpoint of velocity, then they would both produce acceleration (see the "Average Rate of Change (Contextualized)" blue section).
I.V Uniformly Accelerated Motion.
Finally, the first unquestionably Physics-specific content can be described after several preliminary sections. All of the previously covered material can be found in other, not necessarily Physics-focused courses, from freshman Calculus to an 8th grade science unit covering the scientific method and uncertainty - now comes the time for the explicit Physics proper, where the skills learned over the previous sections will come into full use.
The following section, regarding Uniformly Accelerated Motion, entails the basic fundamental equations that govern motion (when ignoring things like drag/air resistance - see Subsection III.IV for that), and can be used for both one-dimensional and two-dimensional motion (see Subsection III.III for 2D).
#
P. Rule .
Uniformly Accelerated Motion:
The Uniformly Accelerated Motion (U.A.M.) equations, also known as the Kinematic equations, are a set of four equations that can be used when a given object/system is moving with a constant acceleration. In calculus terms, an object is in constant acceleration when the highest exponent of the position equation is 2 or below (a quadratic or smaller). If the highest exponent is three or above, the object is not in Uniformly Accelerated Motion.
If the position equation is not given, but constant acceleration can be otherwise assumed, U.A.M. can be freely used.
Oft used as a memorization tool for the specifications of U.A.M. is the following mantra: There are 5 U.A.M. variables, and there are 4 equations. If you know 3 variables, you can find the other 2, leaving 1 happy Physics student.
If you are analyzing the movements of two objects, and they share three U.A.M. variable values, then you will know that the other two variables have to be the same as well, and that the movements of the two objects must be identical.
For example, in the classic bullet problem, where a bullet fired horizontally and a bullet dropped from the same height both have a Δy of -h, a y-direction acceleration of -9.81 m/s², and a Viy of 0, it can easily be determined that the rest of the y-direction variables (including the time it would take them to hit the ground) would be the same. This is spite of the fact that the bullets travel different x-distances, as time is the same for the x-direction and y-direction U.A.M. - see Rule 25 and the rest of Projectile Motion for more information.
The Uniformly Accelerated Motion (U.A.M.) equations, also known as the Kinematic equations, are a set of four equations that can be used when a given object/system is moving with a constant acceleration. In calculus terms, an object is in constant acceleration when the highest exponent of the position equation is 2 or below (a quadratic or smaller). If the highest exponent is three or above, the object is not in Uniformly Accelerated Motion.
If the position equation is not given, but constant acceleration can be otherwise assumed, U.A.M. can be freely used.
Oft used as a memorization tool for the specifications of U.A.M. is the following mantra: There are 5 U.A.M. variables, and there are 4 equations. If you know 3 variables, you can find the other 2, leaving 1 happy Physics student.
If you are analyzing the movements of two objects, and they share three U.A.M. variable values, then you will know that the other two variables have to be the same as well, and that the movements of the two objects must be identical.
For example, in the classic bullet problem, where a bullet fired horizontally and a bullet dropped from the same height both have a Δy of -h, a y-direction acceleration of -9.81 m/s², and a Viy of 0, it can easily be determined that the rest of the y-direction variables (including the time it would take them to hit the ground) would be the same. This is spite of the fact that the bullets travel different x-distances, as time is the same for the x-direction and y-direction U.A.M. - see Rule 25 and the rest of Projectile Motion for more information.
# U.A.M. Equations:
U.A.M. allows the physicist to use 5 special equations not allowed otherwise. When using the equations, know that they only account for the displacement in a particular direction, and that the variables for movement in the x and y-directions do not necessarily translate between the directions (with the exception of time, as stated in Rule 25).
Solving for any variables (other than time) with regard to movement in one direction does not mean that you can use the values for that variables for the other direction.
For example - if a rocket is launched directly upward, then the Vf of the y-directional movement will be a very large number, while the Vf of the x-directional movement will be 0.
This is very important information, critical for some applications of U.A.M., such as Profectile Motion, which will be covered shortly. In particular, this directional difference is dealt with in more thorough detail in Subsection III.III.
In summary, IN ANY OF THE GIVEN EQUATIONS, YOU CAN CHANGE DISPLACEMENT TO BE CHANGE IN Y IF THE CIRCUMSTANCES OF THE QUESTION DEMANDS IT.
1. VF = Vi + (a × ∆t).
Velocity Final is equal to velocity initial, plus the acceleration multiplied by the change in time.
2. ∆x = (Vi × ∆t) + ½(a × ∆t²)
Displacement is equal to velocity initial multiplied by the change in time, plus 1/2 multiplied by acceleration and the change in time squared.
3. VF² = Vi² + (2 × a × ∆x)
Velocity final squared is equal to velocity initial squared, plus two multiplied by the acceleration and the displacement.
4. ∆x = ½(VF + Vi) × ∆t
The change in position is equal to one half, times the quantity of velocity final plus velocity initial, times the change in time.
VF = Velocity Final (Instantaneous)
Vi = Velocity Initial (Instantaneous)
a = Acceleration
∆t = Change in Time
∆x = Displacement (or change in position)
Additionally, there are some lame 'alternate' versions of these equations using slightly different variables, useful for deriving and integrating the equations:
v = v0 + at
x = x0 + v0t + ½at²
v² = v0² + 2a(x - x0)
x = x0 + ½(v + v0) × t
# Memorization songs for U.A.M. Equations:
<disclaimer>
I believe that the best way to memorize new information is to associate it with something that we have already memorized that we subconsciously reinforce through repetition: music. Everyone has already memorized hundreds of melodies, so finding one that would match the rhythm and meter of the equation is not too terribly difficult. Of course, fast music is most of the time unfit for memorizing an equation, of which a slower recitation and melody are much easier to perfectly and quickly recall.
</disclaimer>
1. To the theme of Funiculì, Funiculà (Slower part):
Vf equals vi + a times change in t.
2. To the theme of Funiculì, Funiculà (Faster Part):
Change in, x equals, vi times change in t. plus one, half times, a, change in t squared.
vi times change in t equals vi times the change in t!
vi times change in t plus one half times a change in t, squared,
vi times change in t plus one half times a change-in-t squared.
3. To the theme of Mozart's Dies Irae:
Vf squared equals, (da da da da) vi squared plus, (da da da da) 2 times a times, change in x equals vi SQUARED plus 2a change in time.
4. To the theme of Satie's Gnossienne No. 5
Delta x, ~~~~ equals one slash two, ~~~~~~~~~~~~~~~ times velocity final plus vi, times change, in time...
# Esoteric U.A.M. Problem:
A use of the U.A.M. equations that is not immediately apparent:
Two trains, each having a constant speed of 30 km/h, are headed toward eachother on the same straight track. A bird that can fly 60 km/h flies off the front of one train when they are 60 km apart and heads directly for the other train. Upon reaching the other train, the (crazy) bird flies directly back to the first train, and so forth. What is the total distance traveled by the bird before the trains collide?
Answer(s):
60 km
Explanation:
This question has several traits that force the physicist to utilize critical thinking skills instead of just plugging in numbers into formulas mindlessly, which one may get in the habit of if asked too many uninspired questions.
For one, velocity cannot replace speed in most circumstances due to the inherent differences of velocity using straight-line difference and speed using the total distance traveled, but there is one exception: If the object (or objects, in this case) travel in a straight-line, which is to say in one dimension, then the speed is equal to the velocity and they are interchangeable, atleast with regard to magnitude (since velocity is a vector). This is stated in the speed definition.
Utilizing vector addition (see Rule 16) would not work, because the directions would cause the train velocities to cancel out.
The specific parameters of the problem make it easier to solve: imagine the trains as being simple objects with directionless speed (as stated in the problem), for example. From the perspective of the conductor of the first train, the second train is going 60 kilometers per hour, relative to the first train. We can replace the entire two train scenario (which has perfect symmetry and identical U.A.M. variables) and replace it with a single moving object - the trains are individually moving 30 km/hr towards eachother at a starting distance of 60 km from eachother, and as such are equivalent to a single train moving at 60 km/hr toward a brick wall 60 km away. Mathematically, these conclusions can be derived as follows, as a unique result of the symmetry between the movement of the trains:
SpeedTotal = Speed1 + Speed2
SpeedTotal = 30 km/hr + 30 km/hr
SpeedTotal = 60 km/hr
Thus, in this question, ViT and VFT are in reference to the single moving train, and are both equal to 60 km/hr. Additionally, the change in x (displacement) has been changed to 60 km, and considering the doubled speed of the single train, this works out perfectly with the original scenario. Since there are three known U.A.M. variables, we can find the other two.
For this question only, it is more logical to remain in km/hr instead of converting into m/s as is the usual.
We will first try to determine the acceleration using the train's U.A.M. equations - each U.A.M. equation has acceleration, so it is needed to get what is really wanted: the change in time.
VF1² = Vi1² + 2 × a × ∆x
(60 km/hr)² = (60 km/hr)² + 2 × a × 60 km.
0 = 2 × a × 60 km.
a = 0
This simplifies things significantly, and was totally obvious considering that the final velocity is the same as the initial velocity. Thus, for the second equation, which has two parts, both with the change in time (and the second with acceleration as a multiplier, nullifying it), the 2nd U.A.M. equation is best suited for this scenario, as it can quickly isolate the change in time.
∆x = Vi1 × ∆t + ½(a × ∆t²)
60 km = (60 km/hr) × ∆t
∆t = 1
This is the last real mathematical step - lastly, some dreaded logic must be performed. If we were to consider the flying bird, we would find that it is flying at the same speed as the train and would thus go 60 km/hr for one hour before crashing into the wall, which is clearly equal to 1 hours worth of flight and thus 60 km of flight distance. Regardless of the original red herring complexity of how the bird would be moving back and forth between the trains, all one really needs to understand is that the bird will fly for 60 minutes at 60 km/hr before the trains hit eachother. Indeed, this problem has a hidden trick to solving it, although it is not necessary for some.
# WARNING:
KNOWLEDGE REGARDING CALCULUS-CONCEPTS SUCH AS DERIVATIVES WILL BECOME FULLY PREREQUISITE IN THE NEXT PHYSICS SECTION (II). MAKE SURE YOU KNOW ATLEAST THE DERIVATIVE PART OF SINGLE-VARIABLE CALCULUS BEFORE CONTINUING ONTO FREE FALL.
II. Free Fall.
II.I Intro to Free Fall.
- The only force acting on it is the Force of Gravity.
- It is not touching any other objects.
- There is no air resistance (the object is falling in a vacuum).
If an object meets all these requirements and is in free fall, then it would have a constant gravitational acceleration relative to the gravitational pull of the planet/celestial object it is on. On Earth for example, the acceleration of all objects in free fall is -9.81 m/s² in the y-direction. See Rule 14 for more information.
#
P. Rule .
Gravitational Acceleration:
gEarth = 9.81 m/s² (when in free fall)
The Acceleration due to Gravity on any planet or space thing is described using the variable 'g'. In and of itself, g cannot be negative as it merely represents an attractive force acting upon an object.
On Earth, for example, the gravitational pull of the planet is described as gEarth = 9.81 m/s². From a global perspective, gEarth is not constant at all locations on the planet. However, from a local perspective, the acceleration due to gravity is constant, and should always be considered as such when solving a problem.
Never accidentally use gEarth for another planet. Other planets/celestial objects have their own gravitational acceleration constants which will likely be given by the problem (or left as an exercise for the reader to determine). For example, gMars = 3.73 m/s².
The acceleration due to gravity, g, is the same no matter the mass of the object. The mass of the planet, however, will alter g as the gravitational pull of the planet will differ.
ay Earth = -9.81 m/s² (when in free fall)
When direction is considered in relation to the gravitational pull, and the xy-plane upon which the object exists is acknowledged (as it will be in practically all Physics problems), then the downward gravitational pull towards the center of the planet will produce a negative acceleration relative to the object's plane (when in free fall).
Thus, ay, the Acceleration due to Gravity in the Y-direction (for free fall on planet earth), is -9.81 m/s², or -g. Note that this can also be represented as 9.81 m/s² Down, but NEVER as -9.81 m/s² Down (which is in effect 9.81 m/s² Up, or reverse gravity).
No matter the positioning of the object (if its tilted or not), the acceleration due to gravity will remain pointed directly downward towards the center of the planet/celestial body. Additionally, note that gravitational force (the force causing the acceleration), which will be described in Section VI, is also always pointed directly downward towards the center of the planet regardless of whether the object is tilted or not; See Rule 60.
The Acceleration due to Gravity must not be confused with the Acceleration due to Gravity in the Y-direction. In practice, the former, g alone (without the negative), will be used much more often in Physics problems, especially when performing free-body problems involving the force of gravity (discussed later on in Subsection VI.II).
g = Acceleration due to Gravity.
ay = Acceleration due to Gravity in the Y-direction.
gEarth = 9.81 m/s². (when in free fall)
ay Earth = -9.81 m/s² (when in free fall)
gEarth = 9.81 m/s² (when in free fall)
The Acceleration due to Gravity on any planet or space thing is described using the variable 'g'. In and of itself, g cannot be negative as it merely represents an attractive force acting upon an object.
On Earth, for example, the gravitational pull of the planet is described as gEarth = 9.81 m/s². From a global perspective, gEarth is not constant at all locations on the planet. However, from a local perspective, the acceleration due to gravity is constant, and should always be considered as such when solving a problem.
Never accidentally use gEarth for another planet. Other planets/celestial objects have their own gravitational acceleration constants which will likely be given by the problem (or left as an exercise for the reader to determine). For example, gMars = 3.73 m/s².
The acceleration due to gravity, g, is the same no matter the mass of the object. The mass of the planet, however, will alter g as the gravitational pull of the planet will differ.
ay Earth = -9.81 m/s² (when in free fall)
When direction is considered in relation to the gravitational pull, and the xy-plane upon which the object exists is acknowledged (as it will be in practically all Physics problems), then the downward gravitational pull towards the center of the planet will produce a negative acceleration relative to the object's plane (when in free fall).
Thus, ay, the Acceleration due to Gravity in the Y-direction (for free fall on planet earth), is -9.81 m/s², or -g. Note that this can also be represented as 9.81 m/s² Down, but NEVER as -9.81 m/s² Down (which is in effect 9.81 m/s² Up, or reverse gravity).
No matter the positioning of the object (if its tilted or not), the acceleration due to gravity will remain pointed directly downward towards the center of the planet/celestial body. Additionally, note that gravitational force (the force causing the acceleration), which will be described in Section VI, is also always pointed directly downward towards the center of the planet regardless of whether the object is tilted or not; See Rule 60.
The Acceleration due to Gravity must not be confused with the Acceleration due to Gravity in the Y-direction. In practice, the former, g alone (without the negative), will be used much more often in Physics problems, especially when performing free-body problems involving the force of gravity (discussed later on in Subsection VI.II).
g = Acceleration due to Gravity.
ay = Acceleration due to Gravity in the Y-direction.
gEarth = 9.81 m/s². (when in free fall)
ay Earth = -9.81 m/s² (when in free fall)
#
P. Rule .
Splitting U.A.M. Calculations:
Sometimes, when you are dealing with an object in free fall that changes direction (such as when gravity pulls down an upward initially thrown upward), splitting your calculations into two parts (or more!) is necessary in order to find information that serves the problem as a whole.
For example, if you were to take a ball and throw it up in the air, catching it at the same y-value that you threw it, the change in position would be 0, making it impossible to find the change in time using the entirety of the event. Thus, one has to split the movement of the object into the periods before and after it passed the critical point (the point mid-air in which the ball stops moving upward and effectively pauses for a moment before it begins falling), with the period of the ball moving upward and the period of it falling downward being dealt with separately in calculations (different U.A.M. sessions as it were, which may share some variables but represent different periods of movement).
After separation, the values from the different sessions can be stitched together to provide a more complete view of the entire movement sequence of the object. The total change in time for the example event, if the ball lands in the same place where it was thrown, would be the change in time of either half of the event doubled, due to symmetry. If the ball lands somewhere other than where it was thrown, then the time for each half would have to be calculated and then added together to find the total time.
Sometimes, when you are dealing with an object in free fall that changes direction (such as when gravity pulls down an upward initially thrown upward), splitting your calculations into two parts (or more!) is necessary in order to find information that serves the problem as a whole.
For example, if you were to take a ball and throw it up in the air, catching it at the same y-value that you threw it, the change in position would be 0, making it impossible to find the change in time using the entirety of the event. Thus, one has to split the movement of the object into the periods before and after it passed the critical point (the point mid-air in which the ball stops moving upward and effectively pauses for a moment before it begins falling), with the period of the ball moving upward and the period of it falling downward being dealt with separately in calculations (different U.A.M. sessions as it were, which may share some variables but represent different periods of movement).
After separation, the values from the different sessions can be stitched together to provide a more complete view of the entire movement sequence of the object. The total change in time for the example event, if the ball lands in the same place where it was thrown, would be the change in time of either half of the event doubled, due to symmetry. If the ball lands somewhere other than where it was thrown, then the time for each half would have to be calculated and then added together to find the total time.
# Common Mistakes in Free Fall:
1. When you throw a ball upward, that does not mean that it will have a positive acceleration. Having such would make it shoot upward like a rocket. Gravity is a positive constant, but the acceleration in the y-direction during free fall is -9.81 m/s² for any object, regardless of whether it is moving upward or downward (and if it is moving upward in free fall, it is sure as hell to start moving downward soon thereafter!). See Rule 14 for more information regarding gravitational acceleration.
2. Objects thrown upward do not have an initial velocity of 0 (atleast in the y-direction) - they already have a positive velocity before being thrown due to the force applied by whatever is throwing them. An initial velocity of zero in the y-direction will not cause an object to move upward - the initial velocity must be positive.
3. The force with which an object is thrown will not effect the acceleration in the y-direction. Regardless of whether a ball is dropped or thrown downward, the acceleration in the y direction will be -9.81 m/s², and only the position and velocity will change to reflect this force. If an object is thrown down at 100 km/hr, it will be accelerating as fast as an object that was only dropped, because while acceleration affects velocity, velocity does not affect gravitational acceleration.
III. Vectors and Projectile Motion
III.I Vector Basics.
# Scalar: A quantity that has magnitude only. Examples include distance, speed, time, volume, and density. Inherently, every magnitude is a scalar.
#
P. Rule .
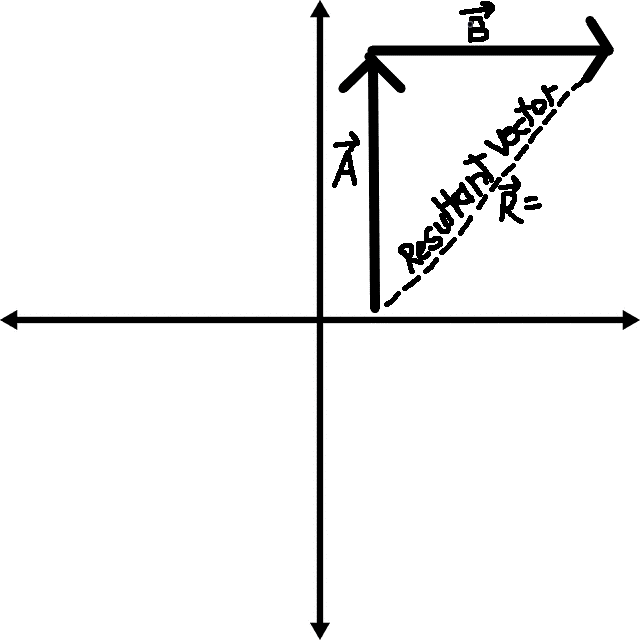
Introductory Tip-to-Tail Vector Addition:
Vector addition is not simply adding the magnitude of the vectors together, but using the pythagorean theorem to find the line that connects the given vectors when they are placed tail-to-tip. This tells you the resultant vector.
If the vectors are in perfect cardinal direction, as is the example below, then of course pythagorean theorem can be quickly applied. Otherwise, using vector decomposition (see Rule 18) is the easiest way to create a right triangle for use in the pythagorean theorem, unless you want to use the Law of Cosines.
Here are two vectors utilizing the vector symbols:
A = 49 (mm/s) North
B = 42 (mm/s) East
In order to solve for the resultant vector, some geometry would need to be performed:
a² + b² = c²
C² = A² + B²
||C|| = √A² + B²
||C|| = 65 mm/s.
Since a vector has direction, we need to find it trigonometrically:
tanθ = (O / A) = (B / A) = (42 / 49)
θ = tan⁻¹(42/49) = 40.601° = East of North (see Rule 17).
Thus, the object is moving at a resultant vector of 65 mm/s East of North.
Vector addition is not simply adding the magnitude of the vectors together, but using the pythagorean theorem to find the line that connects the given vectors when they are placed tail-to-tip. This tells you the resultant vector.
If the vectors are in perfect cardinal direction, as is the example below, then of course pythagorean theorem can be quickly applied. Otherwise, using vector decomposition (see Rule 18) is the easiest way to create a right triangle for use in the pythagorean theorem, unless you want to use the Law of Cosines.
Here are two vectors utilizing the vector symbols:
A = 49 (mm/s) North
B = 42 (mm/s) East
In order to solve for the resultant vector, some geometry would need to be performed:
a² + b² = c²
C² = A² + B²
||C|| = √A² + B²
||C|| = 65 mm/s.
Since a vector has direction, we need to find it trigonometrically:
tanθ = (O / A) = (B / A) = (42 / 49)
θ = tan⁻¹(42/49) = 40.601° = East of North (see Rule 17).
Thus, the object is moving at a resultant vector of 65 mm/s East of North.
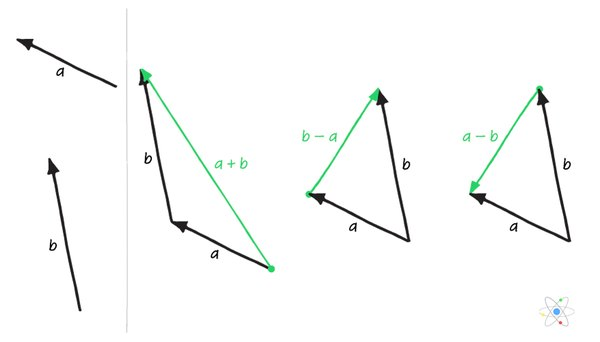
# Vector subtraction:
Vector subtraction is similar to addition. A - B = A + (-B). Thus, all that would need to be done for vector subtraction is to put B in the opposite direction and discover the resultant vector from there. This, indeed, can be a different resultant vector from vector addition - gander: An illustration of the differences between vector addition and subtraction. Courtesy of Sciencing.
#
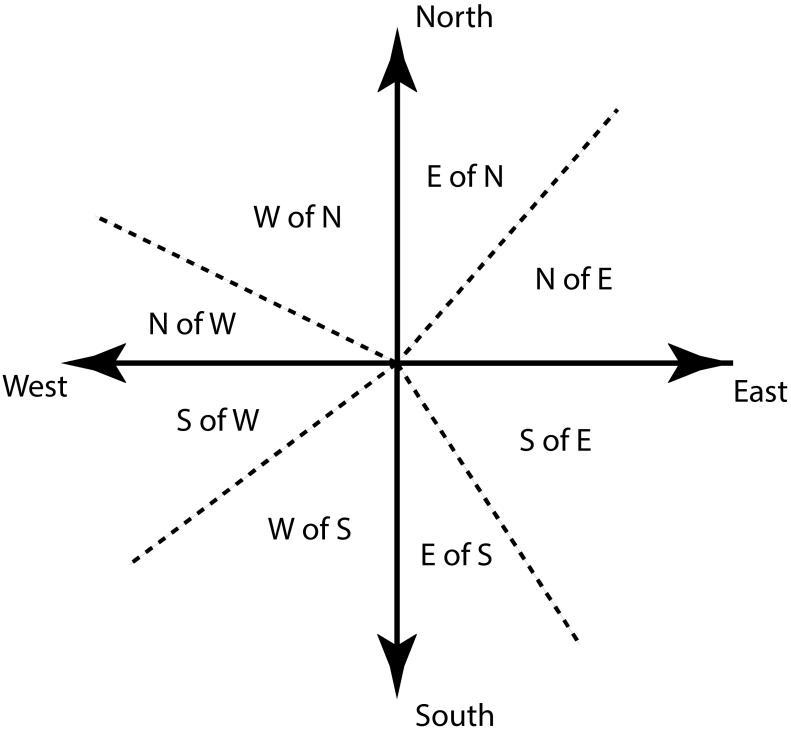
P. Rule .
Cardinal directions in Vectors are as follows:
A graph with most of the cardinal directions of vectors filled in. Courtesy of Flipping Physics.
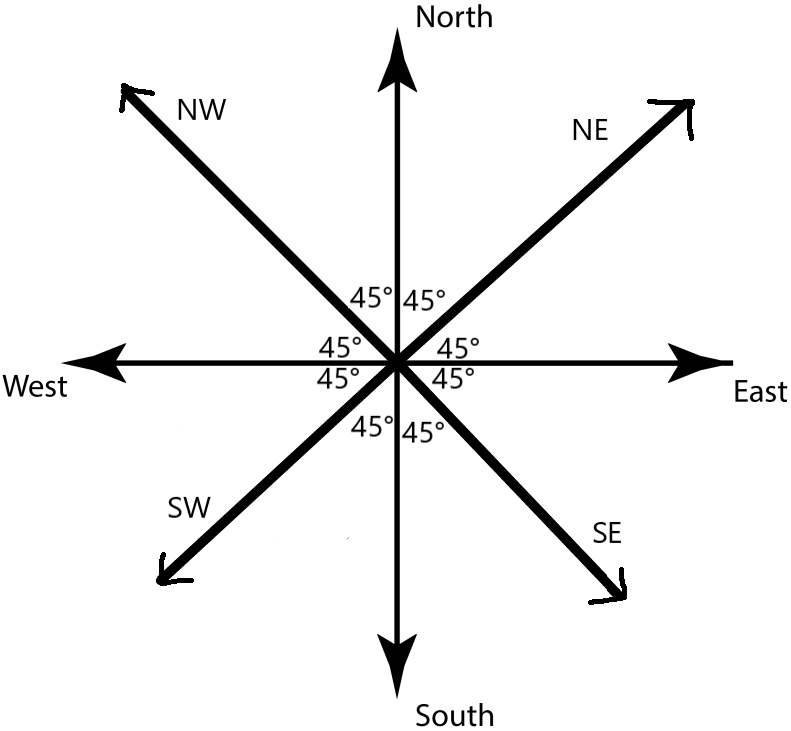
Additionally, the cardinal directions at perfect 45° angles would be as follows:
A graph with the cardinal directions at 45° filled in.
A graph with most of the cardinal directions of vectors filled in. Courtesy of Flipping Physics.
Additionally, the cardinal directions at perfect 45° angles would be as follows:
A graph with the cardinal directions at 45° filled in.
#
P. Rule .
Complex vector problems oftentimes entail vector decomposition, where one may have to use trigonometry in order to find the sides of the vector triangle. A 'component' in any direction can be found for a vector, so long as that component is not perpendicular to the vector - only in that direction is there no component.
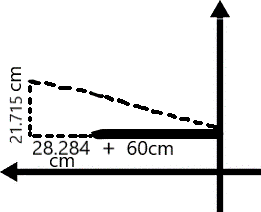
Take this North of East vector for example:
d = 90.0 cm @ 32° N of E.
The vector d has two component vectors, dx and dy.
sinθ = (O / H) = (dy / d)
dy = dsinθ = 90sin(32) = 47.693 ≈ 48cm.
cosθ = (A / H) = (dx / d)
dx = dcosθ = 90cos(32) = 76.324 ≈ 76cm.
Decomposing a vector is also called "breaking" or "resolving" the vector. The information of the original vector can be derived from the component vectors as well, using inverse tangent and the pythagorean theorem, known as 'recomposition'. If you are having problems with re-forming the resultant vector from the component vectors, remember that the resultant vector can be represented as the diagonals of a rectangle that has the components as its sides. This will strongly help with visualization.
The COMPONENTS of a VECTOR are ALSO VECTORS. There are just in a single direction, represented in unit vectors like so: [0î + 5ĵ] or [5î + 0ĵ] (see Rule 20).
Take this North of East vector for example:
d = 90.0 cm @ 32° N of E.
The vector d has two component vectors, dx and dy.
sinθ = (O / H) = (dy / d)
dy = dsinθ = 90sin(32) = 47.693 ≈ 48cm.
cosθ = (A / H) = (dx / d)
dx = dcosθ = 90cos(32) = 76.324 ≈ 76cm.
Decomposing a vector is also called "breaking" or "resolving" the vector. The information of the original vector can be derived from the component vectors as well, using inverse tangent and the pythagorean theorem, known as 'recomposition'. If you are having problems with re-forming the resultant vector from the component vectors, remember that the resultant vector can be represented as the diagonals of a rectangle that has the components as its sides. This will strongly help with visualization.
The COMPONENTS of a VECTOR are ALSO VECTORS. There are just in a single direction, represented in unit vectors like so: [0î + 5ĵ] or [5î + 0ĵ] (see Rule 20).
#
P. Rule .
The Associative Property of Vector Addition:
A + (B + C) = (A + B) + C.
This property, in conjunction with vector decomposition, is very useful when doing vector problems such as the following:
The initial vector, going from 60 cm West, to 50 cm North, to 40 cm SouthWest.
Through the transposition of the associative property, two sides of the right triangle (of which the hypotenuse is displacement) have been found in terms of vector decompositions.
The two decomposed vector variables have been replaced with their values found through trigonometry. Now, all that would need to be done to find the displacement is the pythagorean theorem.
A + (B + C) = (A + B) + C.
This property, in conjunction with vector decomposition, is very useful when doing vector problems such as the following:
The initial vector, going from 60 cm West, to 50 cm North, to 40 cm SouthWest.
Through the transposition of the associative property, two sides of the right triangle (of which the hypotenuse is displacement) have been found in terms of vector decompositions.
The two decomposed vector variables have been replaced with their values found through trigonometry. Now, all that would need to be done to find the displacement is the pythagorean theorem.
#
P. Rule .
UNIT VECTORS:
Unit vectors are vectors with a magnitude of 1 unit in an absolute direction, without any decomposable angle. They are written differently than normal vectors, with a roof symbol on top rather than an arrow:
î = x̂ = 1 unit in the x direction.
ĵ = ŷ = 1 unit in the y direction.
k̂ = ẑ = 1 unit in the z direction.
Vix ≈ [31.7î + 14.8ĵ] m/s ≈ 35.0 m/s @ 25.0° above horizontal.
This way of writing is simply the pre-decomposed way of writing a vector.
If you have to go from an already decomposed roof form to the exact same form as an answer, it is easy as hell:
A = [2.0î + 2.0ĵ]m
B = [1.0î - 3.0ĵ]m
C = [4.0î + 4.0ĵ]m
R = A + B + C = [7.0î + 3.0ĵ]m
Note that given the component vectors, reconstruction of a direction for the whole vector is possible (obviously), though unless the angle is a perfect 45°, you will only get a general idea of where it is pointing, since 25° North of East is the same as 65° East of North.
Unit vectors are vectors with a magnitude of 1 unit in an absolute direction, without any decomposable angle. They are written differently than normal vectors, with a roof symbol on top rather than an arrow:
î = x̂ = 1 unit in the x direction.
ĵ = ŷ = 1 unit in the y direction.
k̂ = ẑ = 1 unit in the z direction.
Vix ≈ [31.7î + 14.8ĵ] m/s ≈ 35.0 m/s @ 25.0° above horizontal.
This way of writing is simply the pre-decomposed way of writing a vector.
If you have to go from an already decomposed roof form to the exact same form as an answer, it is easy as hell:
A = [2.0î + 2.0ĵ]m
B = [1.0î - 3.0ĵ]m
C = [4.0î + 4.0ĵ]m
R = A + B + C = [7.0î + 3.0ĵ]m
Note that given the component vectors, reconstruction of a direction for the whole vector is possible (obviously), though unless the angle is a perfect 45°, you will only get a general idea of where it is pointing, since 25° North of East is the same as 65° East of North.
#
P. Rule .
When a question asks to find the distance between two vectors, you simply need to find the displacement between their endpoints.
In a mechanism similar to Vector Subtraction, create your own vector that has the base of its tail on the tip of the first vector, and the base of its tip on the tip of the second vector - the order of the vectors does not matter. Call this new vector ∆r, and the two original vectors r1 & r2.
r1 + ∆r = r2
∆r = r2 - r1
You do not need to move either of the original vectors to find the distance between them - you simply need to create a new vector that bridges their endpoints. Then, find the length of that vector by using the pythagorean strategies taught before - see Rule 17 and Rule 18. The vectors may look similar to this:
A graph with two vectors with no other information. Courtesy of Flipping Physics.
A graph with two vectors with no other information, except now with the connecting vector created. Courtesy of Flipping Physics.
From this point, you can either find the answer in terms of unit vectors or in terms of magnitude & direction. Of course, the unsimplified unit vector form will always be faster and simpler. Here is an example problem carried out to fruition using unit vectors:
In a mechanism similar to Vector Subtraction, create your own vector that has the base of its tail on the tip of the first vector, and the base of its tip on the tip of the second vector - the order of the vectors does not matter. Call this new vector ∆r, and the two original vectors r1 & r2.
r1 + ∆r = r2
∆r = r2 - r1
You do not need to move either of the original vectors to find the distance between them - you simply need to create a new vector that bridges their endpoints. Then, find the length of that vector by using the pythagorean strategies taught before - see Rule 17 and Rule 18. The vectors may look similar to this:
A graph with two vectors with no other information. Courtesy of Flipping Physics.
A graph with two vectors with no other information, except now with the connecting vector created. Courtesy of Flipping Physics.
From this point, you can either find the answer in terms of unit vectors or in terms of magnitude & direction. Of course, the unsimplified unit vector form will always be faster and simpler. Here is an example problem carried out to fruition using unit vectors:
r1 = 15.0m @ 55.0° E of N
r2 = 25.0m @ 45.0° N of E
r1 = [r1sinθ1î + r1cosθ1ĵ]
= [(15)sin(55)î + (15)cos(55)ĵ]m
= [12.2872î + 8.60365ĵ]m
r2 = [r2cosθ2î + r2sinθ2ĵ]
= [(25)cos(45)î + (25)sin(45)ĵ]m
= [17.6777î + 17.6777ĵ]m
Δr = r2 − r1 = [12.2872î + 8.60365ĵ] − [17.6777î + 17.6777ĵ]
= Δr = [5.39040î + 9.07405ĵ]m
Because change in r is also change in position, this vector is also the displacement between the two original vectors:
Δr ≈ [5.39î + 9.07ĵ]m
||Δr|| = √(5.39040)² + (9.07405)²
||Δr|| = 10.5544 ≈ 10.6m
#
P. Rule .
The r position vector, r, is used to identify the location of an object in multiple dimensions.
r = xî + yĵ + zk̂ identifies the location of an object in 3-dimensional space.
Δr = rf - ri is the displacement of an object in 3-dimensional space.
Δr/Δt = vaverage & dr/dt = vinstantaneous
Δv/Δt = aaverage & dv/dt = ainstantaneous
r = xî + yĵ + zk̂ identifies the location of an object in 3-dimensional space.
Δr = rf - ri is the displacement of an object in 3-dimensional space.
Δr/Δt = vaverage & dr/dt = vinstantaneous
Δv/Δt = aaverage & dv/dt = ainstantaneous
III.II Rotation & Multiplication.
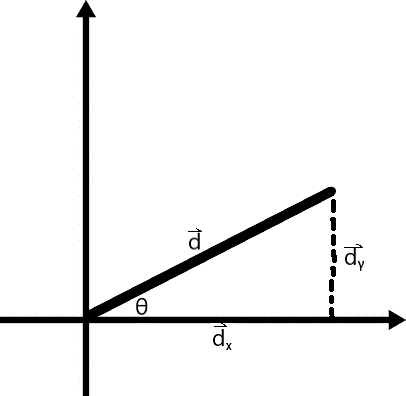
# Vector Rotation:
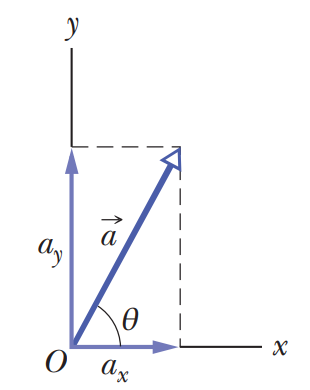
The coordinate system you are familiar with has the x and y axes parallel to the sides of the page. When you have a vector (lets name it a) on this natural coordinate system, the components of the vectors are going to parallel to the sides of the page as well.
The vector a with its component vectors and the angle theta.
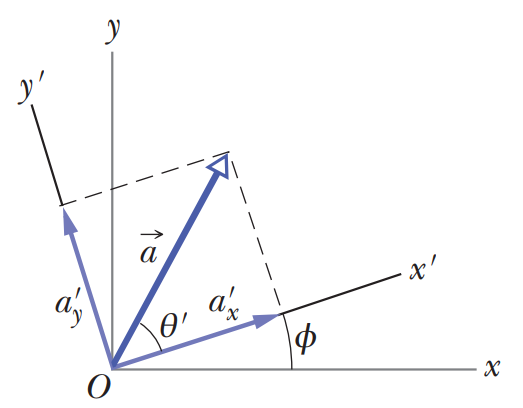
If you were to rotate the axes (but not the vector a) through an angle ϕ as shown below, the components would have new values, a'x and a'y. Since there are an infinite number of choices of ϕ, there are an infinite number of different pairs of components for a:
The coordinate axes of vector a having been tilted and afforded new component vectors.
||a|| = √(aₓ)² + (aᵧ)²
||a|| = √(a'ₓ)² + (a'ᵧ)²
Also,
θ = θ′ + ϕ
The relations among vector do not depend on the location of the origin nor on the orientation of the axes.
# ==Multiplying Vectors==
There are three types of vector muliplication. The first type is multiplying a vector by a scalar, which gives a vector. The other two multiply a vector by a vector, of which you have two choices: Taking the 'dot product' of two vectors gives a scalar answer, while taking the 'cross product' gives a new vector that is perpendicular to the original two, the direction of which can be determined using the right-hand rule.The best way to understand the difference between dot product and cross product beyond their scalar/vector nature is to consider when their products are minimized or maximized (described in each section). As a simple memorization tool, always remember that a · a = (|a|)², or the magnitude of a squared, while a × a = 0. The reasons for this are obvious once you analyze each multiplication tool in full.
# Multiplying a Vector by a Scalar:
The product of the scalar s and a vector v is a new vector whose magnitude is sv, and whose direction is the same as that of v if s is positive, and opposite that of v if s is negative. To divide v by s, multiply v by 1/s.
# Multiplying a Vector by a Vector:
# P. WoO "Vector by Vector"-1: DOT PRODUCT: SCALAR.
Equation:
a · b = abcosϕ
a, b = The magnitudes of a and b, respectively.
cosϕ = The angle between a and b. Because the dot product uses cosine, which is an even trig. function (cos(-ϕ) = cos(ϕ)), dot product is commutative: a · b = b · a. This is not true with the cross product, which uses sine, an odd function.
Definition:
The value given by Dot Product is a scalar, and you can see this through how each term on the right side of the equation is a directionless scalar value.
If ϕ < 90°, then the result of the dot product is positive.
If ϕ = 90°, then the result of the dot product is 0.
If ϕ > 90°, then the result of the dot product is negative.
If the angle ϕ is 0°, then the component of one vector is at a maximum, and thus also is the dot product of the vectors.
If, instead, ϕ is 90°, the component of one vector along the other is zero, and so is the dot product.
If ϕ is 180° (the vectors are parallel) dot product is maximized, and if vectors are perpendicular (90°), the result is zero. Cross product is the opposite.
# P. WoO "Vector by Vector"-2: DOT PRODUCT - TRIPLE VECTORS: SCALAR.
If either or both of the vectors are 3-dimensional, you must utilize unit-vector notation. In this state, their dot product would be
a · b = (aₓî + aᵧĵ + azk̂) · (bₓî + bᵧĵ + bzk̂)
a · b = aₓbₓ + aᵧbᵧ + azbz
This will give THE EXACT SAME ANSWER as the original equation if you are only using two-dimensions, and will save you a lot of time if you are very lazy. Ignore the fact that we are not really 'distributing' the terms as you normally do with the distributive law. Unit Vectors are unique.
# P. WoO "Vector by Vector"-3: CROSS PRODUCT: VECTOR.
Equation:
Finding the magnitude for vector product is similar to that of dot product:
a × b = absinϕ
a, b = The magnitudes of a and b, respectively.
sinϕ = The angle between a and b. Because the cross product uses sine, an odd trig function, cross product is NOT commutative: a × b = -(b × a). This is the opposite of the dot product, which uses an even function.
Definition:
Finding the magnitude of the resultant vector of a cross product is easy - Finding the angle/direction is easy with extra steps.
If ϕ = 90°, then the cross product is maximized.
If ϕ = 0° or 180°, then the cross product is 0.
If 0 < ϕ < 180° or if -360° < ϕ < -180°, then the cross product is positive.
If 180° < ϕ < 360° or if -180° < ϕ < 0, then the cross product is negative.
If the vectors are parallel or antiparallel, then the cross product results in a zero vector.
The magnitude of a × b, which can be written as |a × b|, is maximum when a and b are perpendicular to eachother.
If the vector is parallel, the resultant magnitude is 0, and if it is perpendicular, the result is maximized. Dot product is the opposite.
# P. WoO "Vector by Vector"-4: CROSS PRODUCT - DIRECTION.
The direction of cross product is pointing in the n̂ direction, where n̂ ⊥ â and n̂ ⊥ b̂. You can easily determine the direction of a cross product, perpendicular to the two vectors, using the "Right-hand Rule":
A demonstration of the right hand rule. Courtesy of Wikimedia.
The easiest way to think about it is this: Use the positioning of the right hand as shown in the images below and above. Do not forget that the cross product is non-commutative, and so it 100% matters which vectors you assign your fingers. Middle finger is A, pointer finger is B, thumb is C. If you were to do this same thing on your left hand, you would get B × A instead of A × B - it just works backwards.
Twist your hand so that your fingers are pointing in the correct direction of the vectors - this does not mean that your fingers have to look exactly like the graph, only that they must be in the correct direction as their respective vectors. Your thumb, resultant vector c, will be pointing in the direction of the cross product.
You can use this system for visualizing the x, y, and z directions as well. The Right-hand uses a right coordinate system, as opposed to a left coordinate system, which would necessitate using the left hand. These systems are merely different visualizations of the x-y-z plane.
The difference between the Left and Right-hand Rules, and how to visualize them on the x-y-z plane.
# P. WoO "Vector by Vector"-5: CROSS PRODUCT - TRIPLE VECTORS: VECTOR.
If either or both of the vectors are 3-dimensional, you must utilize unit-vector notation. In this state, their cross product would be
a × b = (aₓî + aᵧĵ + azk̂) · (bₓî + bᵧĵ + bzk̂)
But we do not simplify to isolate every x, y, and z coefficient as we did with Dot Product. Instead, we are going to use a matrix, or rather a 3x3 determinant ([[[[[[[[).
A matrix in which the vector components of a and b are multiplied and subtracted from one another.
Starting from the unit vectors on top, the variables in green are multiplied, and those in red are subtracted from the ones in green, all within the specific unit vector they are attached to. Thus, from this matrix (WHICH SHOULD EASILY BE SET TO MEMORY FOR FUTURE REFERENCE) we can discern the following equation:
a × b = (aᵧbz - bᵧaz)î + (azbₓ - bzaₓ)ĵ + (aₓbᵧ - bₓaᵧ)k̂
III.III Projectile Motion.
#
P. Rule .
Projectile Motion - A specialization of Free Fall in which the object is moving in multiple dimensions. Thus, this movement has all of the properties of free fall in place:
- The only force acting on it is the Force of Gravity.
- It is not touching any other objects.
- There is no air resistance (the object is falling in a vacuum).
- The object has Uniformly Accelerated Motion, and thus can have all of the U.A.M. equations applied.
When solving a problem like this, you would need to separate your known variables in the x and y directions. The equations that describe the motions of an object in projectile motion are different in the x direction and the y direction. Various things placed in their appropriate columns include:
X-direction ┃ Y-Direction
━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━━
ax = 0 ┃ Free-Fall
Constant Velocity ┃ ay = -g = -9.81(m/s²)
Vx = (∆x / ∆t) ┃ U.A.M.
┃
(Needs 2 Var.) (Needs 3 Var.)
In projectile motion, the object will not accelerate to the left or to the right, it will have a constant velocity only. The localized gravity here on Earth makes it only give the y direction of a falling object acceleration.
If you were to drop an object straight downward, the constant velocity would be zero as it would not move in the x or y direction whatsoever. It would also not be in projectile motion, as it is only moving in one dimension.
If the object were to be thrown however, the object would have a non-zero constant velocity and would be in projectile motion.
- The only force acting on it is the Force of Gravity.
- It is not touching any other objects.
- There is no air resistance (the object is falling in a vacuum).
- The object has Uniformly Accelerated Motion, and thus can have all of the U.A.M. equations applied.
When solving a problem like this, you would need to separate your known variables in the x and y directions. The equations that describe the motions of an object in projectile motion are different in the x direction and the y direction. Various things placed in their appropriate columns include:
X-direction ┃ Y-Direction
━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━━
ax = 0 ┃ Free-Fall
Constant Velocity ┃ ay = -g = -9.81(m/s²)
Vx = (∆x / ∆t) ┃ U.A.M.
┃
(Needs 2 Var.) (Needs 3 Var.)
In projectile motion, the object will not accelerate to the left or to the right, it will have a constant velocity only. The localized gravity here on Earth makes it only give the y direction of a falling object acceleration.
If you were to drop an object straight downward, the constant velocity would be zero as it would not move in the x or y direction whatsoever. It would also not be in projectile motion, as it is only moving in one dimension.
If the object were to be thrown however, the object would have a non-zero constant velocity and would be in projectile motion.
#
P. Rule .
- Differing equations for free fall in the X-direction and Y-directions:
1. VF = Vi
The first equation simplifies the velocity of x in projectile motion to a single variable, Vx, which we already intuitively knew.
2. ∆x = Vi × ∆t
Substituting in Vx, as discovered in the first equation, gives us the following:
∆x = Vx × ∆t
Upon further inspection, one should be able to identify this equation as merely being the standard velocity equation: Vx = (∆x / ∆t)
Thus, the velocity equation itself must be the one used when calculating movement in the x direction during projectile motion. Since there are only 3 variables, you would need to know 2 variables to discover the other 1.
X-DIRECTION:
Since the acceleration for projectile motion in the x-direction is always zero, and every U.A.M. equation has acceleration, after plugging in zero for acceleration for each one we are left with only two equations:1. VF = Vi
The first equation simplifies the velocity of x in projectile motion to a single variable, Vx, which we already intuitively knew.
2. ∆x = Vi × ∆t
Substituting in Vx, as discovered in the first equation, gives us the following:
∆x = Vx × ∆t
Upon further inspection, one should be able to identify this equation as merely being the standard velocity equation: Vx = (∆x / ∆t)
Thus, the velocity equation itself must be the one used when calculating movement in the x direction during projectile motion. Since there are only 3 variables, you would need to know 2 variables to discover the other 1.
Y-DIRECTION:
For the y direction, the equations are the same as they have always been - all four U.A.M. equations are in play with acceleration as -9.81 m/s², and you need three variables to find the other two. This simplifies the process.
#
P. Rule .
The only U.A.M. variable that is a scalar is change in time (∆t). If you solve for the change in time in the y or x direction, you can use it for the other direction. This is because ∆t is independent of direction as a scalar.
#
P. Rule .
When you need to find the final velocity of an object in projectile motion, you need to find the velocity in the y direction and the velocity in the x direction. Then, you must realize that since you have the x and y components of an objects movement, that you have the decomposed vector and now need to find the vector itself, the hypotenuse of the triangle through the pythagorean theorem.
NEVER FORGET to find the direction at the end - you just have to do the sine inverse (or cosine inverse depending on which theta you need, though the theta should always be on the tail of the vector/hypotenuse) using the x and y decomposed vectors. This will give you the angle that, if you don't have any particular directions to work off of at the beginning, can just be said to be 'in front of the negative y-axis' if the object is moving rightward and downward, changing this as needed.
Remember that angles also must follow sig. fig. rules no matter what.
Vectors always require direction in addition to magnitude, a + or - will not do.
NEVER FORGET to find the direction at the end - you just have to do the sine inverse (or cosine inverse depending on which theta you need, though the theta should always be on the tail of the vector/hypotenuse) using the x and y decomposed vectors. This will give you the angle that, if you don't have any particular directions to work off of at the beginning, can just be said to be 'in front of the negative y-axis' if the object is moving rightward and downward, changing this as needed.
Remember that angles also must follow sig. fig. rules no matter what.
Vectors always require direction in addition to magnitude, a + or - will not do.
#
P. Rule .
As an object falls, the magnitude of the velocity increases and the direction of the velocity points farther and farther directly downward. The velocity vector arrow increases in length as the object falls, because the magnitude of the object's velocity will keep increasing (neglecting air resistance and the existence of a terminal velocity).
#
P. Rule .
Any U.A.M. variable that is a vector (everything other than time) can be decomposed to find its x and y-direction component vectors. This is most useful when you need to find the movement of an object in both directions during projectile motion. For example, if an object were to be launched with an initial speed of 3.25 m/s at an angle of 61.7°, you can easily find the initial velocity in the x-direction and y-direction by using decomposition tricks - see Rule 18.
#
P. Rule .
When doing calculations with unit vectors, as could be done in the previous question, the 2nd U.A.M. equation (and all others, for that matter) can be easily converted into a more useful form:
rF = ri + Vi × t + (1/2) × a × t²
Of course, this equation was created by recognizing r as being the displacement (∆x), and splitting it into its final and initial forms and moving the initial to the right side, as can be done for ∆x or acceleration at any time. Whereas before we were not writing the vector symbols in the U.A.M. equations, we are taking specific note of their vector status now.
'r' is a displacement vector, representing the change in position of the object - see Rule 22 for more uses of it. ri and rF are position vectors, in that they describe the object's location at specific points in time, each being the sum of its components in the x and y directions (and potentially z direction in 3D space). ri and rF are of course representative of the initial and final positions of the object, respectively. The displacement vector r indicates the direct path and distance between these two positions.
Recall that when you are working in unit vectors, U.A.M. equations are done with the x and y component vectors of each vector. For example, Vi can have the value [1.32î + 4.24ĵ] (or anything of the sort) plugged in to any equation. These form a more fun equation to solve, because you are plugging in the x and y forms simultaneously into the equation (for an example and a neat trick, see Rule 30).
EXTREMELY IMPORTANT, READ THIS:
You can easily get very confused when you draw the curved trajectory of an object in projectile motion, and then you draw a vector with a straight line. No, the vector you drew for whichever variable is not saying that the object moved in that same straight line. That is not what vectors mean - vectors represent direction and magnitude, not the actual path of motion. If you have the initial velocity for an object and you draw the vector to find the x and y components, you are only drawing a visualization of a position vector, (as described above), of how much the velocity or whatever is directed horizontally or vertically.
The vector right triangle is not the actual trajectory of the object on a graph.
The vector right triangle is not the actual trajectory of the object on a graph.
rF = ri + Vi × t + (1/2) × a × t²
Of course, this equation was created by recognizing r as being the displacement (∆x), and splitting it into its final and initial forms and moving the initial to the right side, as can be done for ∆x or acceleration at any time. Whereas before we were not writing the vector symbols in the U.A.M. equations, we are taking specific note of their vector status now.
'r' is a displacement vector, representing the change in position of the object - see Rule 22 for more uses of it. ri and rF are position vectors, in that they describe the object's location at specific points in time, each being the sum of its components in the x and y directions (and potentially z direction in 3D space). ri and rF are of course representative of the initial and final positions of the object, respectively. The displacement vector r indicates the direct path and distance between these two positions.
Recall that when you are working in unit vectors, U.A.M. equations are done with the x and y component vectors of each vector. For example, Vi can have the value [1.32î + 4.24ĵ] (or anything of the sort) plugged in to any equation. These form a more fun equation to solve, because you are plugging in the x and y forms simultaneously into the equation (for an example and a neat trick, see Rule 30).
EXTREMELY IMPORTANT, READ THIS:
You can easily get very confused when you draw the curved trajectory of an object in projectile motion, and then you draw a vector with a straight line. No, the vector you drew for whichever variable is not saying that the object moved in that same straight line. That is not what vectors mean - vectors represent direction and magnitude, not the actual path of motion. If you have the initial velocity for an object and you draw the vector to find the x and y components, you are only drawing a visualization of a position vector, (as described above), of how much the velocity or whatever is directed horizontally or vertically.
The vector right triangle is not the actual trajectory of the object on a graph.
The vector right triangle is not the actual trajectory of the object on a graph.
#
P. Rule .
There is something very beautiful, the result of the independence of the x and y-directions, that must be experienced as a mathematician or Physicist to appreciate its true beauty.
Say you have plugged in the unit vectors for each of the variables in the 2nd U.A.M. equation (see Rule 29 for how this can be done), and you get the following:
[0.93î + yĵ] = [0î + 0ĵ] + [1.54079î + 2.86155ĵ]t + (1/2) × [-9.81ĵ]t²
0.93î + yĵ = 1.54079tî + 2.86155tĵ - 4.905t²ĵ
What I will now do, will be one of the miraculous things you have ever seen in your life, and something you shall remember until your dying days: Because x-direction and y-direction are independent, we can isolate the x-direction by removing everything else:
0.93 = 1.54079t
From here, the process is simple, isolating time and whatnot (which, as we learned in past revelations (Rule 25), is a directionless scalar quantity that can be used in both the x and y directions). Of course, we can repeat this process by isolating the y-direction, where we can now plug in the newly found time.
Say you have plugged in the unit vectors for each of the variables in the 2nd U.A.M. equation (see Rule 29 for how this can be done), and you get the following:
[0.93î + yĵ] = [0î + 0ĵ] + [1.54079î + 2.86155ĵ]t + (1/2) × [-9.81ĵ]t²
0.93î + yĵ = 1.54079tî + 2.86155tĵ - 4.905t²ĵ
What I will now do, will be one of the miraculous things you have ever seen in your life, and something you shall remember until your dying days: Because x-direction and y-direction are independent, we can isolate the x-direction by removing everything else:
0.93 = 1.54079t
From here, the process is simple, isolating time and whatnot (which, as we learned in past revelations (Rule 25), is a directionless scalar quantity that can be used in both the x and y directions). Of course, we can repeat this process by isolating the y-direction, where we can now plug in the newly found time.
#
P. Rule .
Some general tricks that keep one's ducks in line when doing Physakz: When you discover the value of a new variable, always immediately check whether the sign is correct.
1. Your object is falling? The velocity is going to be negative.
2. You found negative time? Time travel doesn't exist yet. Go back and find your error somewhere, which probably has to do with possibility 1.
Additionally, sometimes, specifically when you are finding time in the 2nd U.A.M. equation (where time is squared), you will need to use the quadratic formula. Try to figure any possible way in which you avoid using it, whether using a different formula or whatever. If you have to, you have to, but use your common sense in determining which answer applies to your problem, if only one.
1. Your object is falling? The velocity is going to be negative.
2. You found negative time? Time travel doesn't exist yet. Go back and find your error somewhere, which probably has to do with possibility 1.
Additionally, sometimes, specifically when you are finding time in the 2nd U.A.M. equation (where time is squared), you will need to use the quadratic formula. Try to figure any possible way in which you avoid using it, whether using a different formula or whatever. If you have to, you have to, but use your common sense in determining which answer applies to your problem, if only one.
III.IV Drag.
# Fluid: Anything that can flow, so generally gases and liquids. Any relative velocity between a fluid and a body (either because the body moves through the fluid or because the fluid moves past the body) will cause the body to experience a drag force.
#
P. Rule . My Treatise on Drag (1):
Because projectile motion and free fall have explicit requirements of an object moving through a vacuum, accounting for air resistance means that the object is not in projectile motion or free fall. Thus,
ay ≠ -9.81 m/s²
Vx ≠ Constant
The force of drag always acts opposite to the direction of the velocity of the object: A free body diagram of velocity with the forces of Gravity and the decomposed x and y forces of Drag being shown. Courtesy of Flipping Physics.
There are several equations for drag, each with their own specifications. The equation known simply as the "drag equation" is most commonly used, and is as follows:
Fdrag = (1/2) × ρ × V² × D × A
ρ (rho) = Density of the medium
V = Velocity of the object
D = Drag Coefficient
A = Cross Sectional Area
A: The cross-sectional area of the object is the area of the object normal to the direction of its travel. E.g., when the object is moving directly towards you, what object do you see?
Immediately note that Fdrag is a scalar. Other equations, like the linear drag equation, will result in a vector.
# Analysis:
Take the object to be a ball, for the sake of discussion.
Acircle = πr²
Additionally, let's assume that the following information about the ball:
r = 0.031835 meters
m = 0.14529 kg
Vix = 4.469444 m/s, in the first 1/100th of a second.
D: The drag coefficient is the number used to model all of the complex dependencies of drag on shape, inclination, and some flow conditions. Essentially, it is a number determined through experiment that helps determine an object's drag. Thus, the coefficient will change depending on the shape of the object, the type of fluid flow around the object, and the object's speed.
The drag coefficient for a smooth sphere is 0.5, conveniently.
ρ: The medium in which the object is traveling is of course air, and the density of air can fluctuate due to temperature and pressure differences. The generalized air density we will use is 1.275 kg/m³.
V: Since we know we will be working with the force in the x-direction, we can use Vi and VF interchangeably with VT. As the velocity of the object changes, the drag coefficient will change with it, changing the net force (as shown in the free body diagram) of the ball, and changing the ball's acceleration. Summarized,
∆V → ∆Fnet → ∆a.
↑ ↓
┗━━━━━━━━━━━━━┛
Clearly, the acceleration is not constant throughout this interaction, and so the object would not be in U.A.M.
However, the mathematician Leonhard Euler devised a trick to emulate U.A.M. by splitting the motion of the object into many short-lasting parts, such as 1/100th of a second, under which the acceleration is approximately constant. This is similar to the concept of Riemann sums being used to find the area under the curves, with the more subdivisions, the more accuracy. Let us do some preliminary work to find the net force in the x-direction before utilizing Euler's method:
Σ Fx = -Fdrag x = m × ax
There is only one force in the x-direction, the drag, which is of course going in the opposite direction of the object in the x-direction and so is negative. This is the net force of the ball, and by Newton's Second Law of Motion (see Rule 68), we know that the net force is equal to the mass of the ball times the acceleration in the x-direction. Continuing onward, we can substitute in the drag equation to be equal to mass times acceleration. From there, the algebra is simple, and you just need to plug in all of your variables to find the answer.
As a result, we have found the acceleration in the x-direction, which DOES NOT EXIST in projectile motion. Since you now know acceleration, Velocity initial, and change in time (1/100 sec), you find 4.6805 m/s as your velocity final. Therefore, compared to the Velocity initial of this 0.01 second period of 4.4694, the velocity in the x-direction (which we took to be constant) has decreased by 1.4 thousandths of a meter per second, accounting for air resistance in our calculations and contrary to what the standard U.A.M. equations for projectile motion would suggest.
∆x = xF - xi = Vix × ∆t + (1/2) × ax × (∆t)²
xF = xi + Vix × ∆t + (1/2) × ax × (∆t)²
x = (0)+(4.4694) × (0.01) + (1/2) × (-0.13953) × (0.01)²
= 0.04469 meters
Because projectile motion and free fall have explicit requirements of an object moving through a vacuum, accounting for air resistance means that the object is not in projectile motion or free fall. Thus,
ay ≠ -9.81 m/s²
Vx ≠ Constant
The force of drag always acts opposite to the direction of the velocity of the object: A free body diagram of velocity with the forces of Gravity and the decomposed x and y forces of Drag being shown. Courtesy of Flipping Physics.
There are several equations for drag, each with their own specifications. The equation known simply as the "drag equation" is most commonly used, and is as follows:
Fdrag = (1/2) × ρ × V² × D × A
ρ (rho) = Density of the medium
V = Velocity of the object
D = Drag Coefficient
A = Cross Sectional Area
A: The cross-sectional area of the object is the area of the object normal to the direction of its travel. E.g., when the object is moving directly towards you, what object do you see?
Immediately note that Fdrag is a scalar. Other equations, like the linear drag equation, will result in a vector.
# Analysis:
Take the object to be a ball, for the sake of discussion.
Acircle = πr²
Additionally, let's assume that the following information about the ball:
r = 0.031835 meters
m = 0.14529 kg
Vix = 4.469444 m/s, in the first 1/100th of a second.
D: The drag coefficient is the number used to model all of the complex dependencies of drag on shape, inclination, and some flow conditions. Essentially, it is a number determined through experiment that helps determine an object's drag. Thus, the coefficient will change depending on the shape of the object, the type of fluid flow around the object, and the object's speed.
The drag coefficient for a smooth sphere is 0.5, conveniently.
ρ: The medium in which the object is traveling is of course air, and the density of air can fluctuate due to temperature and pressure differences. The generalized air density we will use is 1.275 kg/m³.
V: Since we know we will be working with the force in the x-direction, we can use Vi and VF interchangeably with VT. As the velocity of the object changes, the drag coefficient will change with it, changing the net force (as shown in the free body diagram) of the ball, and changing the ball's acceleration. Summarized,
∆V → ∆Fnet → ∆a.
↑ ↓
┗━━━━━━━━━━━━━┛
Clearly, the acceleration is not constant throughout this interaction, and so the object would not be in U.A.M.
However, the mathematician Leonhard Euler devised a trick to emulate U.A.M. by splitting the motion of the object into many short-lasting parts, such as 1/100th of a second, under which the acceleration is approximately constant. This is similar to the concept of Riemann sums being used to find the area under the curves, with the more subdivisions, the more accuracy. Let us do some preliminary work to find the net force in the x-direction before utilizing Euler's method:
Σ Fx = -Fdrag x = m × ax
ax = -((1/2) × ρair × (Vix)² × D × A)
ax = -(ρair × (Vix)² × D × (πr²)) / 2m
ax = -(1.275 × 4.4694² × 0.5 × (π × (0.031835)²)) / 2 × (0.14529)
ax = -0.13953 m/s²
There is only one force in the x-direction, the drag, which is of course going in the opposite direction of the object in the x-direction and so is negative. This is the net force of the ball, and by Newton's Second Law of Motion (see Rule 68), we know that the net force is equal to the mass of the ball times the acceleration in the x-direction. Continuing onward, we can substitute in the drag equation to be equal to mass times acceleration. From there, the algebra is simple, and you just need to plug in all of your variables to find the answer.As a result, we have found the acceleration in the x-direction, which DOES NOT EXIST in projectile motion. Since you now know acceleration, Velocity initial, and change in time (1/100 sec), you find 4.6805 m/s as your velocity final. Therefore, compared to the Velocity initial of this 0.01 second period of 4.4694, the velocity in the x-direction (which we took to be constant) has decreased by 1.4 thousandths of a meter per second, accounting for air resistance in our calculations and contrary to what the standard U.A.M. equations for projectile motion would suggest.
∆x = xF - xi = Vix × ∆t + (1/2) × ax × (∆t)²
xF = xi + Vix × ∆t + (1/2) × ax × (∆t)²
x = (0)+(4.4694) × (0.01) + (1/2) × (-0.13953) × (0.01)²
= 0.04469 meters
# TERMINAL VELOCITY:
"The speed at which a falling body will cease accelerating and begin moving at a constant speed downward, as a result of the effects of drag."
As a body falls, the drag force gradually increases in magnitude (from zero) as the speed of the body increases. If the body falls long enough, the force of drag will eventually equal to the force of gravity, ideally. In the real world, the force of gravity will never exactly equal the force of drag, of course, but the acceleration will become small enough that it will be negligible for any calculations.
Though the forces will cancel eachother out, this does not mean that the object will stop moving (see Rule 74 for the Third Law of Motion) - it only means that the object will have no acceleration, and that it will be in equilibrium, in the sense that the velocity will be constant.
From this point onward, the body will fall at a constant speed, known as the terminal velocity VT.
The fall of a cat, and the drag force that will eventually bring it to terminal velocity.
# LINEAR DRAG:
There is a simpler, more memorizable equation for drag that THEY don't want you to know about. It is known as the Linear Drag Equation, and it can only be used for "small objects moving at slow speeds":
Fdrag = -b × v
b = Proportionality constant
v = Velocity of the object
A "Proportionality constant" is just the ratio between two quantities, and here it has the units kg/s.
While the traditional "drag equation" as elaborated previously results in a scalar, this new drag equation results in a vector.
The negative in the equation means that the drag force has the opposite direction of the velocity of the object. Thus, when the object is moving upward on Earth, the force of drag is downward, and when the ball begins falling downward, the force of drag moves upward.
# DRAG ANALYSIS:
As an object moves upward, the acceleration will decrease to -g, because of the following sequence of events:
The object will have a downward acceleration and drag force.
Because of the downward acceleration, the speed of the object will decrease.
Because the speed of the object is decreasing, the magnitude of the drag force will decrease as well, because the drag force is proportional to the square of the velocity.
As the magnitude of the drag force decreases, the magnitude of the net force will decrease as well (as the net force is composed of the acceleration and drag force, which are acting in the same direction here).
Thus, because the net force of the object is decreasing, the acceleration is going to decrease, and when the object is at the top of the parabolar path, it will have an acceleration of -g, and will temporarily have a speed of 0 in the y direction.
When the object moves down, of course, the drag force will grow in the opposite direction of gravity as the objects falls.
Thus, although the speed of the ball is increasing, the magnitude of the net force will be decreasing, seeing how the acceleration and force of drag will increasingly cancel out as the object picks up speed.
Finally, because the magnitude of the net force is decreasing, this means the acceleration is decreasing, and it will be continue decreasing until it reaches zero (or near-zero, at which point the object will be in Terminal Velocity.
What this means:
Because the average acceleration on the way up is lower than the average acceleration on the way down, as has just been proven, and given the object lands at the same height is was thrown (e.g. ∆y is the same going up and going down), then if the only two forces acting on the object are drag and gravity, then
The time it takes for the object to go up a distance will be LESS than the time it takes to go down the same distance.
IV. Range & Relative Motion.
IV.I Basics of Range.
#
P. Rule .
Here is the 'Range' equation, giving you the horizontal displacement (which, you should note, is not written with a Δx, as that would displacement as a whole). There are specific characteristics of a question that will allow you to use the range equation, in the same manner as the U.A.M. equations. If a question explicitly says that an object in projectile motion is landing at the same height which it was thrown (or something to that effect), then the range equation can be used as the displacement in the y direction is zero.
Range = (Vi² × sin(2θi)) / g
R = Range = Δx
Vi = ||Vi|| (Magnitude of Vi)
θi = Initial Angle or Launch Angle
g = Acceleration due to gravity on Earth, POSITIVE 9.81 m/s²
Because both the magnitude and direction of the initial velocity vectors are present in the equation, the initial velocity does not need to be resolved into its components for use in the equation.
g: In projectile motion, ay = -g
g = +9.81 m/s²
ay = -9.81 m/s²
Given this information, we know that the value in the bottom of the equation is not the negative acceleration we are accustomed to, but rather the positive acceleration due to gravity on planet Earth, 9.81 m/s². Because gravity has the dimensions of m/s², the rest of the variables must use the standard meters and seconds for their dimensions, m/s for ||Vi|| and meters for the range itself.
θi: The sine of any angle can never be greater than one. Therefore, the maximum range an angle can have (given the magnitude of the velocity initial is constant, which is should considering this is the x-direction) is discoverable through simply setting the sine value of the equation equal to one:
1 = sin(2θi)
2θi = sin⁻¹(1) = 90°
θi = (90° / 2) = 45°.
Therefore, a launch angle of 45° will give us the maximum range of an object given a constant magnitude of the initial velocity. Any angle other than 45° will give a smaller range.
Furthermore, being familiar with the graph of sin(2θ), we know that any two complementary angles will have the same sine value and range, such as 30° and 60°. Mathematically, this is shown as sin(2θi) = sin(2(90 - θi)).
JUST BECAUSE TWO ANGLES HAVE THE SAME RANGE, THAT DOES NOT MEAN THAT THEY HAVE THE SAME PROJECTILE PATH. An object launched at 60 degrees will go higher than one launched at 30 degrees, but they will end up in the same place.
Range = (Vi² × sin(2θi)) / g
R = Range = Δx
Vi = ||Vi|| (Magnitude of Vi)
θi = Initial Angle or Launch Angle
g = Acceleration due to gravity on Earth, POSITIVE 9.81 m/s²
Because both the magnitude and direction of the initial velocity vectors are present in the equation, the initial velocity does not need to be resolved into its components for use in the equation.
g: In projectile motion, ay = -g
g = +9.81 m/s²
ay = -9.81 m/s²
Given this information, we know that the value in the bottom of the equation is not the negative acceleration we are accustomed to, but rather the positive acceleration due to gravity on planet Earth, 9.81 m/s². Because gravity has the dimensions of m/s², the rest of the variables must use the standard meters and seconds for their dimensions, m/s for ||Vi|| and meters for the range itself.
θi: The sine of any angle can never be greater than one. Therefore, the maximum range an angle can have (given the magnitude of the velocity initial is constant, which is should considering this is the x-direction) is discoverable through simply setting the sine value of the equation equal to one:
1 = sin(2θi)
2θi = sin⁻¹(1) = 90°
θi = (90° / 2) = 45°.
Therefore, a launch angle of 45° will give us the maximum range of an object given a constant magnitude of the initial velocity. Any angle other than 45° will give a smaller range.
Furthermore, being familiar with the graph of sin(2θ), we know that any two complementary angles will have the same sine value and range, such as 30° and 60°. Mathematically, this is shown as sin(2θi) = sin(2(90 - θi)).
JUST BECAUSE TWO ANGLES HAVE THE SAME RANGE, THAT DOES NOT MEAN THAT THEY HAVE THE SAME PROJECTILE PATH. An object launched at 60 degrees will go higher than one launched at 30 degrees, but they will end up in the same place.
# Memorization tool for Range:
I believe that the best way to memorize new information is to associate it with something that we have already memorized that we subconsciously reinforce through repetition: music. Everyone has already memorized hundreds of melodies, so finding one that would match the rhythm and meter of the equation is not too terribly difficult.
1. To the theme of Nessun Dorma:
Velocity initial squared, times sine 2 theta, initial, divided by gravity...
IV.II Frames of Reference.
#
P. Rule .
Relative motion is done with vectors. Imagine a van and a motorcycle driving side by side: the velocity of the van relative to Earth is 24 mi/hr in the East direction. The velocity of the motorcycle relative to the Earth is 13 mi/hr in the East direction. These values would be written thusly:
VvE = 24 mi/hr E
VmE = 13 mi/hr E
In order to find the velocity of the van with respect to the motorcycle, we must use Vvm as the term. This value will be the difference between the two vectors.
VvE = VmE + Vvm
Vvm = VvE - VmE
Vvm = 24 mi/hr E - 13 mi/hr E
Vvm = 11 mi/hr E
You may notice that by taking the negative of the vector, we are in effect reversing its direction. This can be represented by switching the order of the subscripts.
-VmE = VEm
= -13 mi/hr E
= 13 mi/hr W
Therefore, from the point of view of the motorcycle, it would appear that the Earth is moving westward at 13 mi/hr. Finally, in order to solve the velocity of the motorcycle with respect to the van, we simply need to take the negative of the already known value of the motorcycle with respect to van:
Vmv = -Vvm
=-11 mi/hr E
11 mi/hr W
Thus, the van, which is moving faster than the motorcycle, would see the motorcycle as moving backwards (west) as 11 mi/hr.
VvE = 24 mi/hr E
VmE = 13 mi/hr E
In order to find the velocity of the van with respect to the motorcycle, we must use Vvm as the term. This value will be the difference between the two vectors.
VvE = VmE + Vvm
Vvm = VvE - VmE
Vvm = 24 mi/hr E - 13 mi/hr E
Vvm = 11 mi/hr E
You may notice that by taking the negative of the vector, we are in effect reversing its direction. This can be represented by switching the order of the subscripts.
-VmE = VEm
= -13 mi/hr E
= 13 mi/hr W
Therefore, from the point of view of the motorcycle, it would appear that the Earth is moving westward at 13 mi/hr. Finally, in order to solve the velocity of the motorcycle with respect to the van, we simply need to take the negative of the already known value of the motorcycle with respect to van:
Vmv = -Vvm
=-11 mi/hr E
11 mi/hr W
Thus, the van, which is moving faster than the motorcycle, would see the motorcycle as moving backwards (west) as 11 mi/hr.
#
P. Rule .
There is a trick that can be used in all relative motion subscripts: any time you sum two relative motion velocities and they share a common subscript on the inside or the outside, that subscript will cancel out in a specific way. Using a previous example (see Rule 34), we can understand specifically what this means:
Vvm = VvE + VEm
The "E" (Earth) on the inside of the two velocities will cancel out, and because the common subscript was on the inside, the subscripts will combine forwardly into vm.
VvE = VmE + Vvm
With this equation, because the common subscript is on the outside, the resultant subscripts are presented backwardly. Of course, you can switch the order of the terms to make the common subscript be on the inside and get the same answer, but knowledge of these tricks either way will be very helpful.
Vvm = VvE + VEm
The "E" (Earth) on the inside of the two velocities will cancel out, and because the common subscript was on the inside, the subscripts will combine forwardly into vm.
VvE = VmE + Vvm
With this equation, because the common subscript is on the outside, the resultant subscripts are presented backwardly. Of course, you can switch the order of the terms to make the common subscript be on the inside and get the same answer, but knowledge of these tricks either way will be very helpful.
# KINEMATICS POSTMORTEM:
We have now come to the end of Non-Rotational Kinematics (atleast, what I will consider 'Non-Rotational Kinematics' in my notes), our studies in Vector Addition, Projectile Motion, Relative Motion, and everything else. Let us review the similarities between the vector decompositions of the various motions: The core principle behind decomposition is that when a vector is not directly in the x or y direction, break the vector in its components. Why do we do this?
Vector Addition: We create components in order to make a right triangle so we can use the Pythagorean Theorem and the Trigonometric functions.
Projectile Motion: We resolve the initial velocity into components because we use different equations in the X and Y directions for projectile motion. We use the equation for constant velocity in the X direction (because acceleration is zero), and in the Y direction we use the U.A.M. equations for free fall.
Relative Motion: Same as Vector Addition, decompose to make a right triangle.
For ever and ever, you will use vectors and vector decomposition in your daily life, because if you are not living as a physicist, are you truly living?
V. Rotational Motion.
V.I Angular & Tangential Velocity.
#
P. Rule .
The position of an object in rotational motion can be determined in Cartesian and Polar coordinates, going back and forth using trigonometry. When an object is moving along a circle with a constant radius, the object undergoes an angular displacement (with regard to the Polar coordinates (r, θ)):
A section of a circle, showcasing arc-length (s), the angle (Δθ), but not the individual angles of the Hypotenuse and the adjacent leg, θF and θi. Courtesy of Wikipedia.
Δθ = θF - θi
The curved linear distance the object would move when moving along an arc is called the arc length. It is the curved length on the side of the circle outside of the angular displacement Δθ. The equation for arc length is as follows:
s = r × Δθ
Where s is the arc length, r is the radius, and Δθ is the angular displacement. THE UNITS FOR ANGULAR DISPLACEMENT MUST BE IN RADIANS. CONVERT USING (π / 180) IF NEEDS BE.
A section of a circle, showcasing arc-length (s), the angle (Δθ), but not the individual angles of the Hypotenuse and the adjacent leg, θF and θi. Courtesy of Wikipedia.
Δθ = θF - θi
The curved linear distance the object would move when moving along an arc is called the arc length. It is the curved length on the side of the circle outside of the angular displacement Δθ. The equation for arc length is as follows:
s = r × Δθ
Where s is the arc length, r is the radius, and Δθ is the angular displacement. THE UNITS FOR ANGULAR DISPLACEMENT MUST BE IN RADIANS. CONVERT USING (π / 180) IF NEEDS BE.
#
P. Rule .
π = 3.1, give or take. It refers to the ratio of a circle's circumference to its diameter, and as an irrational number, it will go on forever. Since the formula for obtaining pi cancels out any dimensions in length (c/d = (86.9m)/(27.5m) ≈ 3.1415926...), the value of pi is in Radians, which is just a dimensionless placeholder unit. The abbreviation for Radians is 'rad'.
#
P. Rule .
While average linear velocity is conveyed as Vavg = (∆x / ∆t), average angular velocity is written as ωavg = (∆θ / ∆t), which can be represented in Radians per Second, Revolutions per Minute, Degrees per Millisecond, etc.
Radians per Second are most commonly used in Physics, while revolutions per minute is most used in Applicationism and "the real world".
Radians per Second are most commonly used in Physics, while revolutions per minute is most used in Applicationism and "the real world".
#
P. Rule .
The symbol for angular acceleration is α, which is very convenient considering how similar it looks to a. The average angular acceleration is equal to αavg = (∆ω / ∆t). Therefore, the units for angular acceleration are radians per second squared or revolutions per minute squared.
#
P. Rule .
Just like how an object can have uniformly accelerated motion, an object can also have uniformly angularly accelerated motion. This is written as U.α.M., instead of U.A.M., even though the alpha is lowercase. As with linear acceleration, the U.α.M. constants can be used when α is constant. All of the variables from U.A.M. must be converted into their angular form:
ωF, ωi, α, ∆θ, and ∆t.
Now, we can rewrite every U.A.M. equation using these variables:
ωF = ωi + (α × ∆t).
∆θ = (ωi × ∆t) + (1/2 × α × ∆t²)
ωF² = ωi² + (2 × α × ∆θ)
∆θ = (1/2) × (ωF + ωi) × ∆t
ALWAYS use radians in your calculations for U.α.M. equations. Additionally, remember that ωF and ωi are instantaneous angular velocities, as opposed to the average velocity (∆θ / ∆t).
ωF, ωi, α, ∆θ, and ∆t.
Now, we can rewrite every U.A.M. equation using these variables:
ωF = ωi + (α × ∆t).
∆θ = (ωi × ∆t) + (1/2 × α × ∆t²)
ωF² = ωi² + (2 × α × ∆θ)
∆θ = (1/2) × (ωF + ωi) × ∆t
ALWAYS use radians in your calculations for U.α.M. equations. Additionally, remember that ωF and ωi are instantaneous angular velocities, as opposed to the average velocity (∆θ / ∆t).
#
P. Rule .
Since angular velocity, angular acceleration, and change in angular position are vectors, they all have direction. However, since clockwise and counterclockwise are observer-dependent, we use the right-hand rule to determine direction.
# Tangential Velocity: The linear velocity of an object moving in a circle. Given by the equation vt = r × ω. Because it is LINEAR, you use m/s as your base units. Furthermore, notice that none of the values in the equation are vectors - this equation refers purely to the magnitudes of each variable.
#
P. Rule .
The farther along you go on the radius of a circle, the linear distance that point travels when moving through a circle, which is called arc length, will increase. This is in spite of the fact that the angular velocity and angular displacement is the same, regardless of radii length, as each point on the radius covers the same number of degrees in the same amount of time.
The path traveled by each point on the radius will form an internal circle, the point moving around the circumference of this circle. Each point on the radius has a linear velocity when it is moving in the circle, known as tangential velocity, which increases proportionally as the radius and arc length (defined by the formula s = r × Δθ) increase. The tangential velocity is given by the equation vt = r × ω, which, just like the arc length equation, requires radians. The angular velocity in the equation needs to be in radians per second.
See the different internal arc lengths that each radius-length has below:
A diagram of internal circles defined by different points on the radius, of which the arc length differs for the same change in θ. Courtesy of Flipping Physics.
Tangential Velocity is named for how its velocity vector is tangent to the circumference of the circle, perpendicular to the radius. Tangential Acceleration is the exact same way:
The tangential velocity of three separate circle, increasing each time. Courtesy of Flipping Physics.
The path traveled by each point on the radius will form an internal circle, the point moving around the circumference of this circle. Each point on the radius has a linear velocity when it is moving in the circle, known as tangential velocity, which increases proportionally as the radius and arc length (defined by the formula s = r × Δθ) increase. The tangential velocity is given by the equation vt = r × ω, which, just like the arc length equation, requires radians. The angular velocity in the equation needs to be in radians per second.
See the different internal arc lengths that each radius-length has below:
A diagram of internal circles defined by different points on the radius, of which the arc length differs for the same change in θ. Courtesy of Flipping Physics.
Tangential Velocity is named for how its velocity vector is tangent to the circumference of the circle, perpendicular to the radius. Tangential Acceleration is the exact same way:
The tangential velocity of three separate circle, increasing each time. Courtesy of Flipping Physics.
#
P. Rule .
Tangential Acceleration is defined by the following equation:
at = r × α.
Like the equations for arc length and tangential velocity, you must use Radians as your angular quantity. Because it is LINEAR, you use m/s² as your base units. Furthermore, notice that none of the values in the equation are vectors - this equation refers purely to the magnitudes of each variable.
at = r × α.
Like the equations for arc length and tangential velocity, you must use Radians as your angular quantity. Because it is LINEAR, you use m/s² as your base units. Furthermore, notice that none of the values in the equation are vectors - this equation refers purely to the magnitudes of each variable.
#
P. Rule .
On the nature of Tangential Velocity (and others) as a vector:
Imagine a situation in which the radius and angular velocity of a point on the circle are both constant - This just means that the circle is rotating at a constant speed.
If this were to be the case, then the linear velocity of the radius, the tangential velocity, would still not be constant, even though tangential velocity is literally equal to the radius times the angular velocity. This is because tangential velocity is a vector with both magnitude and direction. While the magnitude would be constant, the direction of the tangential velocity would be constantly changing (perpendicular to the radius as it makes it revolution around the circle), and so tangential velocity itself would not be constant. Therefore, the radius has neither a tangential acceleration nor an angular acceleration.
Imagine a situation in which the radius and angular velocity of a point on the circle are both constant - This just means that the circle is rotating at a constant speed.
If this were to be the case, then the linear velocity of the radius, the tangential velocity, would still not be constant, even though tangential velocity is literally equal to the radius times the angular velocity. This is because tangential velocity is a vector with both magnitude and direction. While the magnitude would be constant, the direction of the tangential velocity would be constantly changing (perpendicular to the radius as it makes it revolution around the circle), and so tangential velocity itself would not be constant. Therefore, the radius has neither a tangential acceleration nor an angular acceleration.
V.II Centripetal Velocity.
"Radial Velocity" is just linear velocity, and "Radial Acceleration" refers to Centripetal Acceleration (below).
#
P. Rule .
There is ANOTHER linear acceleration apart from tangential acceleration - there are three total that matter. It is called Centripetal Acceleration, also known as Radial Acceleration. Look at these words:
"Centripetal Acceleration is the linear acceleration that causes the tangential velocity to change direction."
Utterly meaningless on their surface, searching for any possible knowledge in these words is an exercise in futility. However, beyond their nonsensical face-value, an elaboration of these words will reveal their value:
The word 'Centripetal' is derived from "centrum", meaning center, and "petere", meaning to seek. Centripetal acceleration is the acceleration that causes circular motion. Centripetal acceleration is always directed inward to the circle, toward the center. It is a center-seeking linear acceleration. The force inward is what causes circular motion - see Rule 49 for more information.
The equation for Centripetal Acceleration is as follows:
ac = (Vt²) / r
Notice that none of the values in the equation are vectors: this equation refers purely to the magnitudes of each variable.
Through the substitution of the substitution of the equation for Tangential velocity, we can simply the equation further:
= ((r × ω)² / r) = ((r² × ω²) / r) = r × ω²
Because it is LINEAR, you use m/s² as your base units.
"Centripetal Acceleration is the linear acceleration that causes the tangential velocity to change direction."
Utterly meaningless on their surface, searching for any possible knowledge in these words is an exercise in futility. However, beyond their nonsensical face-value, an elaboration of these words will reveal their value:
The word 'Centripetal' is derived from "centrum", meaning center, and "petere", meaning to seek. Centripetal acceleration is the acceleration that causes circular motion. Centripetal acceleration is always directed inward to the circle, toward the center. It is a center-seeking linear acceleration. The force inward is what causes circular motion - see Rule 49 for more information.
The equation for Centripetal Acceleration is as follows:
ac = (Vt²) / r
Notice that none of the values in the equation are vectors: this equation refers purely to the magnitudes of each variable.
Through the substitution of the substitution of the equation for Tangential velocity, we can simply the equation further:
= ((r × ω)² / r) = ((r² × ω²) / r) = r × ω²
Because it is LINEAR, you use m/s² as your base units.
#
P. Rule .
We can extrapolate the known information about circular centripetal acceleration to apply to any curved path an object may follow, and therefore any object moving on a curved path will experience a centripetal acceleration.
When going over the top of a hill or other circular object that can have its forces summed to form the centripetal force (see Rule 49), the normal force will be less than the force of gravity, since you feel less of a normal reaction force from the ground. This is why you feel weightless when you are driving over a hill!
When going over the top of a hill or other circular object that can have its forces summed to form the centripetal force (see Rule 49), the normal force will be less than the force of gravity, since you feel less of a normal reaction force from the ground. This is why you feel weightless when you are driving over a hill!
#
P. Rule .
The whole idea of centripetal acceleration and tangential velocity and acceleration and everything else in rotational motion is that all the equations use all the same variables, and you can connect what you have to what you need by repeatedly plugging in numbers into equations. For example, to find centripetal acceleration (equation below), you tangential velocity, which you need the average angular velocity for, and so on. To really instill this into your brain, stare at the equations for rotational motion until you imagine them every time you see a rotating circle. For a refresher on all three types of acceleration, watch this videos.
#
P. Rule .
By the nature of their equations, Tangential velocity requires the object to be in acceleration (either speeding up or slowing down as it goes around the circle), while Centripetal acceleration only needs the object to be going around in the circle at a constant rate.
#
P. Rule .
Newton's Second Law (see Rule 68) states that net force equals mass times acceleration, or ΣF = m × a. Since it has been determined (see Rule 46) that every object moving on a curved path will have centripetal acceleration, we can apply centripetal acceleration to Newton's Second Law and end up with the equation for Centripetal Force:
ΣF = m × ac
As such, one can substitute in the equation for centripetal acceleration (Rule 45) to get the additionally-useful following equation:
ΣF = (m × Vt²) / r
There are several important rules for comprehending centripetal force:
1) Centripetal Force is not a New Force. Most other forces, such as the force of gravity, tension, friction, and the normal force (Subsections V.II - V.IV), are 'independently-defined' forces, meaning they are not dependent on anything else and exist despite of what humans think is possible or impossible. Centripetal force, on the other hand, is composed out of these bedrock forces, whether by a mixture of them or just one. This is because it is the NET force in the inward direction, the net of all the forces acting in the inward direction.
2) Centripetal Force is never in a Free Body Diagram. Because centripetal force is not a new force, it never appears in a free body diagram. In order to determine the centripetal force, you need to draw out your free body diagram and then sum the forces in the inward direction.
3) In is positive, and out is negative. When you sum the forces in the inward direction, the in direction is positive, while the out direction is negative. This is almost the same for what was done before for summing forces, just now you sum them in relation to the in direction, and set them equal to centripetal acceleration instead of m × a. NEVER attempt to sum forces in the "tangential" direction - there is no such thing (you may be thinking of summing in the y or x directions). Instead, sum your torques (see Rule 124).
ΣF = m × ac
As such, one can substitute in the equation for centripetal acceleration (Rule 45) to get the additionally-useful following equation:
ΣF = (m × Vt²) / r
There are several important rules for comprehending centripetal force:
1) Centripetal Force is not a New Force. Most other forces, such as the force of gravity, tension, friction, and the normal force (Subsections V.II - V.IV), are 'independently-defined' forces, meaning they are not dependent on anything else and exist despite of what humans think is possible or impossible. Centripetal force, on the other hand, is composed out of these bedrock forces, whether by a mixture of them or just one. This is because it is the NET force in the inward direction, the net of all the forces acting in the inward direction.
2) Centripetal Force is never in a Free Body Diagram. Because centripetal force is not a new force, it never appears in a free body diagram. In order to determine the centripetal force, you need to draw out your free body diagram and then sum the forces in the inward direction.
3) In is positive, and out is negative. When you sum the forces in the inward direction, the in direction is positive, while the out direction is negative. This is almost the same for what was done before for summing forces, just now you sum them in relation to the in direction, and set them equal to centripetal acceleration instead of m × a. NEVER attempt to sum forces in the "tangential" direction - there is no such thing (you may be thinking of summing in the y or x directions). Instead, sum your torques (see Rule 124).
#
P. Rule .
Time Constant:
The time constant, τ, is a means of determining the time it takes for an exponential equation to get to a percent of its maximum value, calculated similarly to a half-life. The first time constant is 63.2%, which is a universal constant that must be remembered. It is the result of 1 - (1 / e), exactly. This number comes up with some frequency in physics.
Thus, since the first time constant is 63.2% of the time it takes to reach terminal velocity, then 2τ will be the 86.5%, because it increased by 63.2% of the percent remaining until 100%. 3τ will be 95%, and so on and so on. Every increase in the time constant will make the velocity 63.2% closer to terminal velocity. Thus, it will take 6.91τ for the velocity to be 99.9% of the terminal velocity.
Objects that encounter more air resistance and meet their terminal velocity faster, like coffee filters, will have a small time constant, while an object like a baseball will have a larger time constant.
The time constant, τ, is a means of determining the time it takes for an exponential equation to get to a percent of its maximum value, calculated similarly to a half-life. The first time constant is 63.2%, which is a universal constant that must be remembered. It is the result of 1 - (1 / e), exactly. This number comes up with some frequency in physics.
Thus, since the first time constant is 63.2% of the time it takes to reach terminal velocity, then 2τ will be the 86.5%, because it increased by 63.2% of the percent remaining until 100%. 3τ will be 95%, and so on and so on. Every increase in the time constant will make the velocity 63.2% closer to terminal velocity. Thus, it will take 6.91τ for the velocity to be 99.9% of the terminal velocity.
Objects that encounter more air resistance and meet their terminal velocity faster, like coffee filters, will have a small time constant, while an object like a baseball will have a larger time constant.
#
P. Rule .
Rotational Right-Hand-Rule:
There is a second right-hand rule, one separate from the Vector right hand rule described in the "Multiplying Vectors" part of Subsection III.II. The 2nd R.H.R. is the Rotational Right-Hand-Rule (R.R.H.R.), which is performed somewhat differently. This rule gives you the direction of the Angular Velocity (ω) and the Angular Displacement (∆θ) of an object in centripetal motion, which are always the same and perpendicular to the plane of the object:
1. First, you need to know the direction of the revolution of the circle itself. This means whether the circle is moving clockwise or counter-clockwise. See Rule 52 for explanation as to how other characteristics of the circle, such as how its placement in 3-dimensional space, will affect the result.
2. Now that you have taken note of the movement of the circle, curl the fingers of your right hand in the direction of the movement of the circle.
To curl your hand "in the direction of the movement of the circle" means that the curve of your fingers, from the base to the fingertips, matches the movement of the circle: following the path of the your fingers, towards the fingertips, will be identical to the path of the movement of the circle.
Have no restraint in turning your hand to have the path follow correctly - this can be necessary to obtain the correct direction in Step 3.
3. Once your fingers have been curled correctly, stick out your thumb. Your thumb will be pointing in the direction of the Angular Velocity and Angular Displacement of the centripetal motion.
If you have performed this rule correctly, from your point of view (like the bird's eye view of a flat circle in centripetal motion), a circle moving clockwise will always produce a direction in the negative z-axis direction when using the R.R.H.R., and that using it on a circle moving counter-clockwise will result in the positive z-axis direction.
You may wonder, "Why bother with the R.R.H.R. anyways? Can't you just memorize the direction based on whether the circle is moving clockwise or counter-clockwise?". The issue with doing so is that "clockwise" and "counter-clockwise" are observer-dependent directions, and that they can change from whichever perspective you are looking at the circle from (and a problem can require you to look at it from several). Thus, by using the R.R.H.R., you can easily determine which direction the angular velocity & displacement are in by finding the "angular" direction, which, though it can change in positioning depending on perspective, will always be in the same direction.
For example, if you were to determine on the front side of an object in centripetal motion that its direction is outward, and then when you move to the backside that its direction is inward, you would have found the same direction, just from different perspectives. For all intents and purposes, it remains wise to define one view of the object in centripetal motion as being the "front" view, so that any direction inward can be labeled as being on the negative z-axis and any direction outward as being on the positive z-axis.
There is a second right-hand rule, one separate from the Vector right hand rule described in the "Multiplying Vectors" part of Subsection III.II. The 2nd R.H.R. is the Rotational Right-Hand-Rule (R.R.H.R.), which is performed somewhat differently. This rule gives you the direction of the Angular Velocity (ω) and the Angular Displacement (∆θ) of an object in centripetal motion, which are always the same and perpendicular to the plane of the object:
1. First, you need to know the direction of the revolution of the circle itself. This means whether the circle is moving clockwise or counter-clockwise. See Rule 52 for explanation as to how other characteristics of the circle, such as how its placement in 3-dimensional space, will affect the result.
2. Now that you have taken note of the movement of the circle, curl the fingers of your right hand in the direction of the movement of the circle.
To curl your hand "in the direction of the movement of the circle" means that the curve of your fingers, from the base to the fingertips, matches the movement of the circle: following the path of the your fingers, towards the fingertips, will be identical to the path of the movement of the circle.
Have no restraint in turning your hand to have the path follow correctly - this can be necessary to obtain the correct direction in Step 3.
3. Once your fingers have been curled correctly, stick out your thumb. Your thumb will be pointing in the direction of the Angular Velocity and Angular Displacement of the centripetal motion.
If you have performed this rule correctly, from your point of view (like the bird's eye view of a flat circle in centripetal motion), a circle moving clockwise will always produce a direction in the negative z-axis direction when using the R.R.H.R., and that using it on a circle moving counter-clockwise will result in the positive z-axis direction.
You may wonder, "Why bother with the R.R.H.R. anyways? Can't you just memorize the direction based on whether the circle is moving clockwise or counter-clockwise?". The issue with doing so is that "clockwise" and "counter-clockwise" are observer-dependent directions, and that they can change from whichever perspective you are looking at the circle from (and a problem can require you to look at it from several). Thus, by using the R.R.H.R., you can easily determine which direction the angular velocity & displacement are in by finding the "angular" direction, which, though it can change in positioning depending on perspective, will always be in the same direction.
For example, if you were to determine on the front side of an object in centripetal motion that its direction is outward, and then when you move to the backside that its direction is inward, you would have found the same direction, just from different perspectives. For all intents and purposes, it remains wise to define one view of the object in centripetal motion as being the "front" view, so that any direction inward can be labeled as being on the negative z-axis and any direction outward as being on the positive z-axis.
#
P. Rule .
To determine the angular velocity of an object in centripetal motion when looking at it from the side, as depicted in figure (a) below, you would need to perform the exact same steps of the Rotational Right-Hand-Rule (see Rule 51): curl your fingers in the direction of the movement of the circle, with the added cognizance of the positioning your hand. You must make sure to turn your hand to best reflect the motion of the object, as if the path of your fingers was on the same plane as the object, as seen in figure (b).
An example of how the R.R.H.R. would be carried out with respect to an object in centripetal motion as viewed from the side, in this case producing the positive y-direction. Courtesy of Libretexts.
This enables for directions to be found in the negative and positive x and y directions.
An example of how the R.R.H.R. would be carried out with respect to an object in centripetal motion as viewed from the side, in this case producing the positive y-direction. Courtesy of Libretexts.
This enables for directions to be found in the negative and positive x and y directions.
# Conical Pendulum: A pendulum (a hung weight that can swing freely back and forth in oscillations) that swings circularly, the motion of which forms a conical shape. In these problems, the centripetal motion will be along the horizontal plane (if hanging normally), or whichever plane the problem specifies if moving against gravity.
# Uniform Circular Motion: Centripetal motion at a constant angular velocity. This motion thus has no change in angular velocity, no angular acceleration, nor any tangential acceleration. An object spinning on the y-plane, like a yo-yo, is considered to be in nonuniform circular motion, as the force of tension will always be changing as it moves through the air (weakest when at its maximum height, and strongest at the bottom), in order for the net centripetal acceleration to be conserved. The yo-yo will take longer to move through the top semicircle of the revolution than the bottom, since the tangential speed is greater at the bottom. For a conceptual refresher, watch this video proof.
#
P. Rule .
The acceleration of any object in non-uniform circular motion has two perpendicular components: tangential acceleration and centripetal acceleration. Thus, to determine the absolute magnitude of the acceleration of an object in centripetal motion at any moment, you would simply perform the Pythagorean Theorem with the two component accelerations being a and b.