These are my complete notes for Vectors and Projectile Motion in Classical Mechanics.
I color-coded my notes according to their meaning - All numbered notes (which I call rules) are red, and include examples and the basis for understanding a topic. Definitions are written in green, and other important information (such as large-scale drawings that are better visualized than explained) was written in blue. All of this information is preserved on this page, with logical flow and breaks. I use ascii line drawings sparingly - If I can convey information or a graph using an image online, I will do so.
All of the knowledge present in these notes are filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Vectors and Projectile Motion (Classical Mechanics)
Table Of Contents
III. Vectors and Projectile Motion
III.I Vector Basics.
# Scalar: A quantity that has magnitude only. Examples include distance, speed, time, volume, and density.
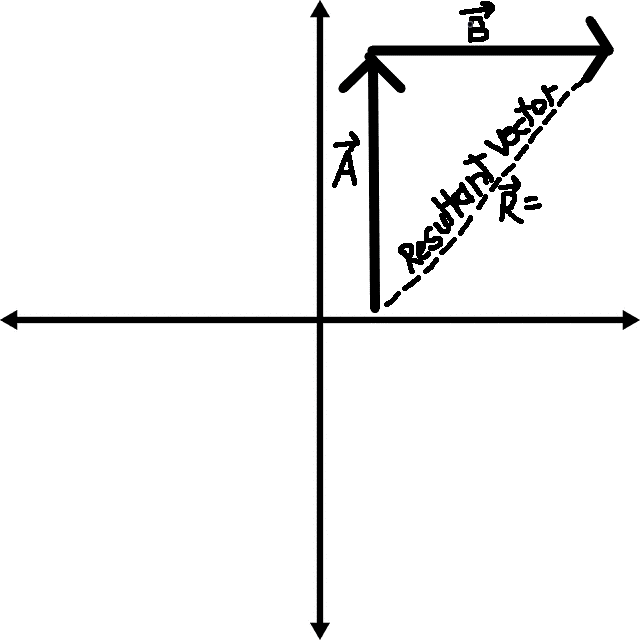
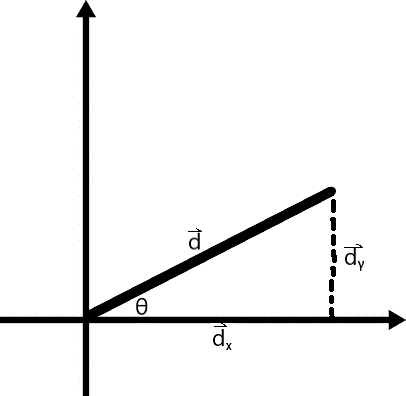
# P. Rule 18. Introductory Tip-to-Tail Vector Addition:
Vector addition is not simply adding the magnitude of the vectors together, but using the pythagorean theorem to find the line that connects the given vectors when they are placed tail-to-tip. This tells you the resultant vector.
If the vectors are in perfect cardinal direction, as is the example below, then of course pythagorean theorem can be quickly applied. Otherwise, using vector decomposition (Rule 20) is the easiest way to create a right triangle for use in the pythagorean theorem, unless you want to use the Law of Cosines.
Here are two vectors utilizing the vector symbols:
A = 49 (mm/s) North
B = 42 (mm/s) East
a² + b² = c²
C² = A² + B²
||C|| = √A² + B²
||C|| = 65 mm/s.
Since a vector has direction, we need to find it trigonometrically:
tanθ = (O / A) = (B / A) = (42 / 49)
θ = tan⁻¹(42/49) = 40.601° = East of North (see rule 19).
Thus, the object is moving at a resultant vector of 65 mm/s East of North.
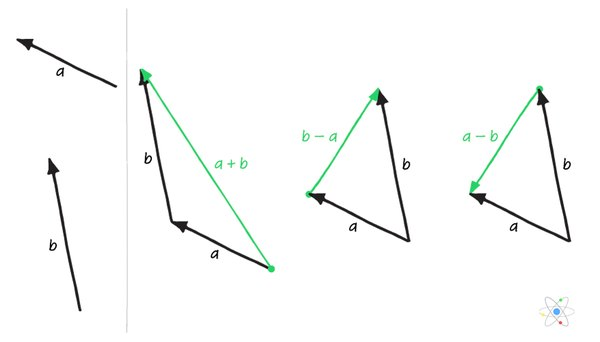
# Vector subtraction:
Vector subtraction is similar to addition. A - B = A + (-B). Thus, all that would need to be done for vector subtraction is to put B in the opposite direction and discover the resultant vector from there. This, indeed, can be a different resultant vector from vector addition - gander:
# P. Rule 19. Cardinal directions in Vectors are as follows:
Additionally, the cardinal directions at perfect 45° angles would be as follows:
# P. Rule 20. Complex vector problems oftentimes entail vector decomposition, where one may have to use trigonometry in order to find the sides of the vector triangle. Take this North of East vector for example:
d = 90.0 cm @ 32° N of E.
sinθ = (O / H) = (dy / d)
dy = dsinθ = 90sin(32) = 47.693 ≈ 48cm.
cosθ = (A / H) = (dx / d)
dx = dcosθ = 90cos(32) = 76.324 ≈ 76cm.
Decomposing a vector is also called "breaking" or "resolving" the vector. The information of the original vector can be derived from the component vectors as well, using inverse tangent and the pythagorean theorem, known as 'recomposition'. If you are having problems with re-forming the resultant vector from the component vectors, remember that the resultant vector can be represented as the diagonals of a rectangle that has the components as its sides. This will strongly help with visualization.
The COMPONENTS of a VECTOR are ALSO VECTORS. There are just in a single direction, represented in unit vectors like so: [0î + 5ĵ] or [5î + 0ĵ] (see Rule 22).
# P. Rule 21. The Associative Property of Vector Addition:
A + (B + C) = (A + B) + C.
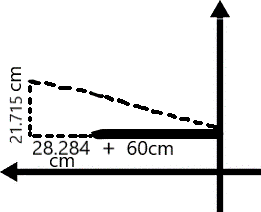
This property, in conjunction with vector decomposition, is very useful when doing vector problems such as the following:
# P. Rule 22. UNIT VECTORS:
Unit vectors are vectors with a magnitude of 1 unit in an absolute direction, without any decomposable angle. They are written differently than normal vectors, with a roof symbol on top rather than an arrow:
î = x̂ = 1 unit in the x direction.
ĵ = ŷ = 1 unit in the y direction.
k̂ = ẑ = 1 unit in the z direction.
Vix ≈ [31.7î + 14.8ĵ] m/s ≈ 35.0 m/s @ 25.0° above horizontal.
This way of writing is simply the pre-decomposed way of writing a vector.
If you have to go from an already decomposed roof form to the exact same form as an answer, it is easy as hell:
A = [2.0î + 2.0ĵ]m
B = [1.0î - 3.0ĵ]m
C = [4.0î + 4.0ĵ]m
R = A + B + C = [7.0î + 3.0ĵ]m
Note that given the component vectors, reconstruction of a direction for the whole vector is possible (obviously), though unless the angle is a perfect 45°, you will only get a general idea of where it is pointing, since 25° North of East is the same as 65° East of North.
# P. Rule 23. When the questions asks to find the distance between two vectors, you can use a simple mechanic:
Create your own vector that has its tail on the tip of the first vector and its tip on the tip of the second vector, call it ∆r.
r1 + ∆r = r2
∆r = r2 - r1
You do not have to move any of the given vectors, you can simply create one that serves the middle an already connected vector would have served in its place. Then, find the displacement (length) of that vector by using the strategies taught in rules 19 and 20. The vectors may look similar to this:
From this point, you can either find the answer in terms of unit vectors or in terms of magnitude in direction. Of course, unit vectors will always be faster and simpler. Here is an example problem carried out to fruition using unit vectors:
r1 = 15.0m @ 55.0° E of N
r2 = 25.0m @ 45.0° N of E
r1 = [r1sinθ1î + r1cosθ1ĵ]
= [(15)sin(55)î + (15)cos(55)ĵ]m
= [12.2872î + 8.60365ĵ]m
r2 = [r2cosθ2î + r2sinθ2ĵ]
= [(25)cos(45)î + (25)sin(45)ĵ]m
= [17.6777î + 17.6777ĵ]m
Δr = r2 − r1 = [12.2872î + 8.60365ĵ] − [17.6777î + 17.6777ĵ]
= Δr = [5.39040î + 9.07405ĵ]m
Because change in r is also change in position, this vector is also the displacement between the two original vectors:
Δr ≈ [5.39î + 9.07ĵ]m
||Δr|| = √(5.39040)² + (9.07405)²
||Δr|| = 10.5544 ≈ 10.6m
# P. Rule 24. The r position vector, r, is used to identify the location of an object in multiple dimensions.
r = xî + yĵ + zk̂ identifies the location of an object in 3-dimensional space.
Δr = rf - ri is the displacement of an object in 3-dimensional space.
Δr/Δt = vaverage & dr/dt = vinstantaneous
Δv/Δt = aaverage & dv/dt = ainstantaneous
III.II Projectile Motion.
- The only force acting on it is the Force of Gravity.
- It is not touching any other objects.
- There is no air resistance (the object is falling in a vacuum).
- The object has Uniformly Accelerated Motion, and thus can have all of the U.A.M. equations applied.
When solving a problem like this, you would need to separate your known variables in the x and y directions. The equations that describe the motions of an object in projectile motion are different in the x direction and the y direction. Various things placed in their appropriate columns include:
X-direction ┃ Y-Direction
━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━━
ax = 0 ┃ Free-Fall
Constant Velocity ┃ ay = -g = -9.81(m/s²)
Vx = (∆x / ∆t) ┃ U.A.M.
┃
(Needs 2 Var.) (Needs 3 Var.)
In projectile motion, the object will not accelerate to the left or to the right, it will have a constant velocity only. The localized gravity here on Earth makes it only give the y direction of a falling object acceleration.
If you were to drop an object straight downward, the constant velocity would be zero as it would not move in the x or y direction whatsoever. It would also not be in projectile motion, as it is only moving in one dimension.
If the object were to be thrown however, the object would have a non-zero constant velocity and would be in projectile motion.
# P. Rule 26. - Differing equations for free fall in the X-direction and Y-directions:
X-DIRECTION:
Since the acceleration for projectile motion in the x-direction is always zero, and every U.A.M. equation has acceleration, after plugging in zero for acceleration for each one we are left with only two equations:1. VF = Vi
The first equation simplifies the velocity of x in projectile motion to a single variable, Vx, which we already intuitively knew.
2. ∆x = Vi × ∆t
Substituting in Vx, as discovered in the first equation, gives us the following:
∆x = Vx × ∆t
Upon further inspection, one should be able to identify this equation as merely being the standard velocity equation: Vx = (∆x / ∆t)
Thus, the velocity equation itself must be the one used when calculating movement in the x direction during projectile motion. Since there are only 3 variables, you would need to know 2 variables to discover the other 1.
Y-DIRECTION:
For the y direction, the equations are the same as they have always been - all four U.A.M. equations are in play with acceleration as -9.81 m/s², and you need three variables to find the other two. This simplifies the process.# P. Rule 27. The only U.A.M. variable that is a scalar is change in time (∆t). If you solve for the change in time in the y or x direction, you can use it for the other direction. This is because ∆t is independent of direction as a scalar.
# P. Rule 28. When you need to find the final velocity of an object in projectile motion, you need to find the velocity in the y direction and the velocity in the x direction. Then, you must realize that since you have the x and y components of an objects movement, that you have the decomposed vector and now need to find the vector itself, the hypotenuse of the triangle through the pythagorean theorem.
NEVER FORGET to find the direction at the end - you just have to do the sin inverse (or cosine inverse depending on which theta you need, though the theta should always be on the tail of the vector/hypotenuse) using the x and y decomposed vectors. This will give you the angle that, if you don't have any particular directions to work off at the beginning, can just be said to 'in front of the negative y-axis' if the object is moving rightward and downward, changing this as needed.
Remember that angles also must follow sig. fig. rules no matter what.
Vectors always require direction in addition to magnitude, a + or - will not do.
# P. Rule 29. As an object falls, the magnitude of the velocity increases and the direction of the velocity points farther and farther down. The velocity vector arrows increase in length as the object falls, because the magnitude of the object's velocity keeps increasing.
# P. Rule 30. Any U.A.M. variable that is a vector (everything other than time) can be decomposed to find its x and y-direction component vectors. This is most useful when you need to find the movement of an object in both directions during projectile motion. For example, if an object were to be launched with an initial speed of 3.25 m/s at an angle of 61.7°, you can easily find the initial velocity in the x-direction and y-direction by using the decomposition tricks of Rule 20.
# P. Rule 31. When doing calculations with unit vectors, as could be done in the previous question, the 2nd U.A.M. equation (and all others, for that matter) can be easily converted into a more useful form:
rF = ri + Vi × t + (1/2) × a × t²
Of course, this equation was created by recognizing r as being the displacement (∆x), and splitting it into its final and initial forms and moving the initial to the right side, as can be done for ∆x or acceleration at any time. Whereas before we were not writing the vector symbols in the U.A.M. equations, we are taking specific note of their vector status now.
'r' is a displacement vector, representing the change in position of the object - see Rule 24 for more uses of it. ri and rF are position vectors, in that they describe the object's location at specific points in time, each being the sum of its components in the x and y directions (and potentially z direction in 3D space). ri and rF are of course representative of the initial and final positions of the object, respectively. The displacement vector r indicates the direct path and distance between these two positions.
Recall that when you are working in unit vectors, U.A.M. equations are done with the x and y component vectors of each vector. For example, Vi can have the value [1.32î + 4.24ĵ] (or anything of the sort) plugged in to any equation. These form a more fun equation to solve, because you are plugging in the x and y forms simultaneously into the equation (for an example and a neat trick, see Rule 32).
EXTREMELY IMPORTANT, READ THIS:
You can easily get very confused when you draw the curved trajectory of an object in projectile motion, and then you draw a vector with a straight line. No, the vector you drew for whichever variable is not saying that the object moved in that same straight line. That is not what vectors mean - vectors represent direction and magnitude, not the actual path of motion. If you have the initial velocity for an object and you draw the vector to find the x and y components, you are only drawing a visualization of a position vector, (as described above), of how much the velocity or whatever is directed horizontally or vertically.
The vector right triangle is not the actual trajectory of the object on a graph.
The vector right triangle is not the actual trajectory of the object on a graph.
# P. Rule 32. There is something very beautiful that is the result of the independence of the x and y-directions - Say you have plugged in the unit vectors for each of the variables in the 2nd U.A.M. equation (in the same fashion as Rule 31), and you get the following:
[0.93î + yĵ] = [0î + 0ĵ] + [1.54079î + 2.86155ĵ]t + (1/2) × [-9.81ĵ]t²
0.93î + yĵ = 1.54079tî + 2.86155tĵ - 4.905t²ĵ
What I will now do, will be one of the miraculous things you have ever seen in your life, and something you shall remember until your dying days: Because x-direction and y-direction are independent, we can isolate the x-direction by removing everything else:
0.93 = 1.54079t
From here, the process is simple, isolating time and whatnot (which, as we learned in the revelations of Rule 27, is a directionless scalar quantity that can be used in both the x and y directions). Of course, we can repeat this process by isolating the y-direction, where we can now plug in the newly found time.
# P. Rule 33. Some general tricks that keep one's ducks in line when doing physakz: When you discover the value of a new variable, always immediately check whether the sign is correct.
1. Your object is falling? The velocity is going to be negative.
2. You found negative time? Time travel doesn't exist yet. Go back and find your error somewhere, which probably has to do with possibility 1.
Additionally, sometimes, specifically when you are finding time in the 2nd U.A.M. equation (where time is squared), you will need to use the quadratic formula. Try to figure any possible way in which you avoid using it, whether using a different formula or whatever. If you have to, you have to, but use your common sense in determining which answer applies to your problem, if only one.
III.III Rotation & Multiplication.
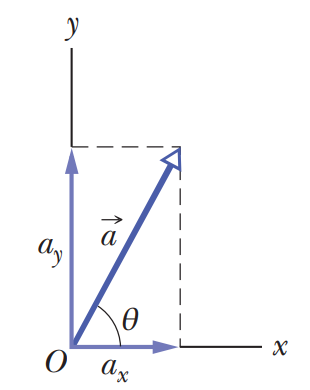
# Vector Rotation:
The coordinate system you are familiar with has the x and y axes parallel to the sides of the page. When you have a vector (lets name it a) on this natural coordinate system, the components of the vectors are going to parallel to the sides of the page as well.
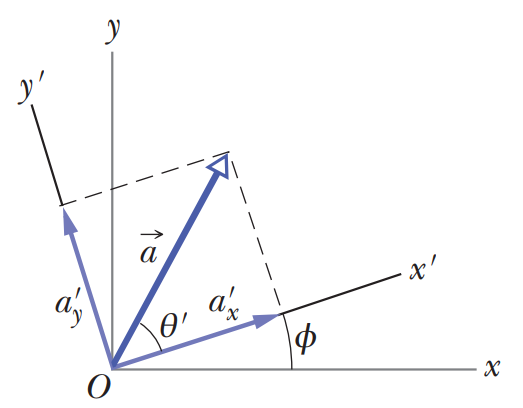
If you were to rotate the axes (but not the vector a) through an angle ϕ as shown below, the components would have new values, a'x and a'y. Since there are an infinite number of choices of ϕ, there are an infinite number of different pairs of components for a:
||a|| = √(aₓ)² + (aᵧ)²
||a|| = √(a'ₓ)² + (a'ᵧ)²
Also,
θ = θ′ + ϕ
The relations among vector do not depend on the location of the origin nor on the orientation of the axes.
# ==Multiplying Vectors==
There are three types of vector muliplication. The first type is multiplying a vector by a scalar, which gives a vector. The other two multiply a vector by a vector, of which you have two choices: Taking the 'dot product' of two vectors gives a scalar answer, while taking the 'cross product' gives a new vector that is perpendicular to the original two, the direction of which can be determined using the right-hand rule.The best way to understand the difference between dot product and cross product beyond their scalar/vector nature is to consider when their products are minimized or maximized (described in each section). As a simple memorization tool, always remember that a · a = (|a|)², or the magnitude of a squared, while a × a = 0. The reasons for this are obvious once you analyze each multiplication tool in full.
# Multiplying a Vector by a Scalar:
The product of the scalar s and a vector v is a new vector whose magnitude is sv, and whose direction is the same as that of v if s is positive, and opposite that of v if s is negative. To divide v by s, multiply v by 1/s.
# Multiplying a Vector by a Vector:
# DOT PRODUCT:
Simply put, in only two dimensions,
a · b = abcosϕ
a and b being the magnitudes of a and b, respectively.
ϕ represents the angle between a and b.
The value given by Dot Product is a scalar, and you can see this through how each term on the right side of the equation is a directionless scalar value. If the angle ϕ between two vectors is 0°, the component of one vector along the other is maximum, and so also is the dot product of the vectors. If, instead, ϕ is 90°, the component of one vector along the other is zero, and so is the dot product. READ: If the vectors are parallel, dot product is maximized, and if vectors are perpendicular, the result is zero. Cross product is the opposite.
VERY IMPORTANT: The commutative law applies to the dot product. Thus,
a · b = b · a
This is not true with cross product.
Triple Vectors - If either or both of the vectors are 3-dimensional, you must utilize unit-vector notation. In this state, their dot product would be
a · b = (aₓî + aᵧĵ + azk̂) · (bₓî + bᵧĵ + bzk̂)
a · b = aₓbₓ + aᵧbᵧ + azbz
This will give THE EXACT SAME ANSWER as the original equation if you are only using two-dimensions, and will save you a lot of time if you are very lazy. Ignore the fact that we are not really 'distributing' the terms as you normally do with the distributive law. Unit Vectors are unique.
# CROSS PRODUCT:
Determining the magnitude of the resultant vector is easy - determining the angle/direction of the resultant vector is easy with extra steps.
Finding the magnitude for vector product is similar to that of dot product:
a × b = c
c = absinϕ
Of course, a and b are the magnitudes of a and b, respectively.
ϕ represents the angle between a and b.
The value given by Cross Product is a vector, so the direction must be calculated in addition to the magnitude. If a and b are parallel or antiparallel, a × b = 0. The magnitude of a × b, which can be written as |a × b|, is maximum when a and b are perpendicular to each other. READ: If the vector is parallel, the resultant magnitude is 0, and if it is perpendicular, the result is maximized. Dot product is the opposite.
VERY IMPORTANT: The commutative law DOES NOT apply to the scalar product. Thus,
a × b ≠ b × a
Instead,
a × b = -(b × a) This is the opposite of the dot product.
The direction of cross product is pointing in the n̂ direction, where n̂ ⊥ â and n̂ ⊥ b̂. You can easily determine the direction of a cross product, perpendicular to the two vectors, using the "Right-hand Rule":
You can use this system for visualizing the x, y, and z directions as well. The Right-hand uses a right coordinate system, as opposed to a left coordinate system, which would necessitate using the left hand. These systems are merely different visualizations of the x-y-z plane.
Triple Vectors - If either or both of the vectors are 3-dimensional, you must utilize unit-vector notation. In this state, their cross product would be
a × b = (aₓî + aᵧĵ + azk̂) · (bₓî + bᵧĵ + bzk̂)
But we do not simplify to isolate every x, y, and z coefficient as we did with Dot Product. Instead, we are going to use a matrix ([[[[[[[[).
Starting from the unit vectors on top, the variables in green are multiplied, and those in red are subtracted from the ones in green, all within the specific unit vector they are attached to. Thus, from this matrix (WHICH SHOULD EASILY BE SET TO MEMORY FOR FUTURE REFERENCE) we can discern the following equation:
a × b = (aᵧbz - bᵧaz)î + (azbₓ - bzaₓ)ĵ + (aₓbᵧ - bₓaᵧ)k̂
III.IV Drag.
# Fluid: Anything that can flow, so generally gases and liquids. Any relative velocity between a fluid and a body (either because the body moves through the fluid or because the fluid moves past the body) will cause the body to experience a drag force.
# P. Rule 34. My Treatise on Drag (1):
Because projectile motion and free fall have explicit requirements of an object moving through a vacuum, accounting for air resistance means that the object is not in projectile motion or free fall. Thus,
ay ≠ -9.81 m/s²
Vx ≠ Constant
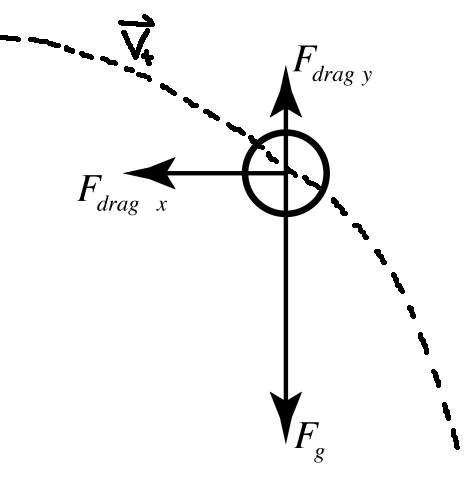
The force of drag always acts opposite to the direction of the velocity of the object:
There are several equations for drag, each with their own specifications. The equation known simply as the "drag equation" is most commonly used, and is as follows:
Fdrag = (1/2) × ρ × V² × D × A
ρ (rho) = Density of the medium
V = Velocity of the object
D = Drag Coefficient
A = Cross Sectional Area
A: The cross-sectional area of the object is the area of the object normal to the direction of it's travel. E.g., when the object is moving directly towards you, what object do you see?
Immediately note that Fdrag is a scalar. Other equations, like the linear drag equation, will result in a vector.
# Analysis:
Take the object to be a ball, for the sake of discussion.
Acircle = πr²
Additionally, let's assume that the following information about the ball:
r = 0.031835 meters
m = 0.14529 kg
Vix = 4.469444 m/s, in the first 1/100th of a second.
D: The drag coefficient is the number used to model all of the complex dependencies of drag on shape, inclination, and some flow conditions. Essentially, it is a number determined through experiment that helps determine an object's drag. Thus, the coefficient will change depending on the shape of the object, the type of fluid flow around the object, and the object's speed.
The drag coefficient for a smooth sphere is 0.5, conveniently.
ρ: The medium in which the object is traveling is of course air, and the density of air can fluctuate due to temperature and pressure differences. The generalized air density we will use is 1.275 kg/m³.
V: Since we know we will be working with the force in the x-direction, we can use Vi and VF interchangeably with VT. As the velocity of the object changes, the drag coefficient will change with it, changing the net force (as shown in the free body diagram) of the ball, and changing the ball's acceleration. Summarized,
∆V → ∆Fnet → ∆a.
↑ ↓
┗━━━━━━━━━━━━━┛
Clearly, the acceleration is not constant throughout this interaction, and so the object would not be in U.A.M.
However, the mathematician Leonhard Euler devised a trick to emulate U.A.M. by splitting the motion of the object into many short-lasting parts, such as 1/100th of a second, under which the acceleration is approximately constant. This is similar to the concept of Riemann sums being used to find the area under the curves, with the more subdivisions, the more accuracy. Let us do some preliminary work to find the net force in the x-direction before utilizing Euler's method:
Σ Fx = -Fdrag x = m × ax
ax = -((1/2) × ρair × (Vix)² × D × A)
ax = -(ρair × (Vix)² × D × (πr²)) / 2m
ax = -(1.275 × 4.4694² × 0.5 × (π × (0.031835)²)) / 2 × (0.14529)
ax = -0.13953 m/s²
There is only one force in the x-direction, the drag, which is of course going in the opposite direction of the object in the x-direction and so is negative. This is the net force of the ball, and by Newton's Second Law of Motion (see Rule 70), we know that the net force is equal to the mass of the ball times the acceleration in the x-direction. Continuing onward, we can substitute in the drag equation to be equal to mass times acceleration. From there, the algebra is simple, and you just need to plug in all of your variables to find the answer.As a result, we have found the acceleration in the x-direction, which DOES NOT EXIST in projectile motion. Since you now know acceleration, Velocity initial, and change in time (1/100 sec), you find 4.6805 m/s as your velocity final. Therefore, compared to the Velocity initial of this 0.01 second period of 4.4694, the velocity in the x-direction (which we took to be constant) has decreased by 1.4 thousandths of a meter per second, accounting for air resistance in our calculations and contrary to what the standard U.A.M. equations for projectile motion would suggest.
∆x = xF - xi = Vix × ∆t + (1/2) × ax × (∆t)²
xF = xi + Vix × ∆t + (1/2) × ax × (∆t)²
x = (0)+(4.4694) × (0.01) + (1/2) × (-0.13953) × (0.01)²
= 0.04469 meters
# TERMINAL VELOCITY:
"The speed at which a falling body will cease accelerating and begin moving at a constant speed downward, as a result of the effects of drag."
As a body falls, the drag force gradually increases in magnitude (from zero) as the speed of the body increases. If the body falls long enough, the force of drag will eventually equal to the force of gravity, ideally. In the real world, the force of gravity will never exactly equal the force of drag, of course, but the acceleration will become small enough that it will be negligible for any calculations.
Though the forces will cancel eachother out, this does not mean that the object will stop moving (see Rule 76 for the Third Law of Motion) - it only means that the object will have no acceleration, and that it will be in equilibrium, in the sense that the velocity will be constant.
From this point onward, the body will fall at a constant speed, known as the terminal velocity VT.
# LINEAR DRAG:
There is a simpler, more memorizable equation for drag that THEY don't want you to know about. It is known as the Linear Drag Equation, and it can only be used for "small objects moving at slow speeds":
Fdrag = -b × v
b = Proportionality constant
v = Velocity of the object
A "Proportionality constant" is just the ratio between two quantities, and here it has the units kg/s.
While the traditional "drag equation" as elaborated previously results in a scalar, this new drag equation results in a vector.
The negative in the equation means that the drag force has the opposite direction of the velocity of the object. Thus, when the object is moving upward on Earth, the force of drag is downward, and when the ball begins falling downward, the force of drag moves upward.
# DRAG ANALYSIS:
As an object moves upward, the acceleration will decrease to -g, because of the following sequence of events:
The object will have a downward acceleration and drag force.
Because of the downward acceleartion, the speed of the object will decrease.
Because the speed of the object is decreasing, the magnitude of the drag force will decrease as well, because the drag force is proportional to the square of the velocity.
As the magnitude of the drag force decreases, the magnitude of the net force will decrease as well (as the net force is composed of the acceleration and drag force, which are acting in the same direction here).
Thus, because the net force of the object is decreasing, the acceleration is going to decrease, and when the object is at the top of the parabolar path, it will have an acceleration of -g, and will temporarily have a speed of 0 in the y direction.
When the object moves down, of course, the drag force will grow in the opposite direction of gravity as the objects falls.
Thus, although the speed of the ball is increasing, the magnitude of the net force will be decreasing, seeing how the acceleration and force of drag will increasingly cancel out as the object picks up speed.
Finally, because the magnitude of the net force is decreasing, this means the acceleration is decreasing, and it will be continue decreasing until it reaches zero (or near-zero, at which point the object will be in Terminal Velocity.
What this means:
Because the average acceleration on the way up is lower than the average acceleration on the way down, as has just been proven, and given the object lands at the same height is was thrown (e.g. ∆y is the same going up and going down), then if the only two forces acting on the object are drag and gravity, then
The time it takes for the object to go up a distance will LESS than the time it takes to go down the same distance.
