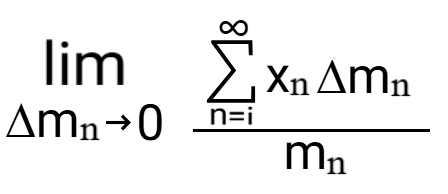These are my complete notes for Momentum & Center of Mass in Classical Mechanics.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Momentum & Center of Mass (Classical Mechanics)
Table Of Contents
VIII. Momentum & Center of Mass
VIII.I Center of Mass.
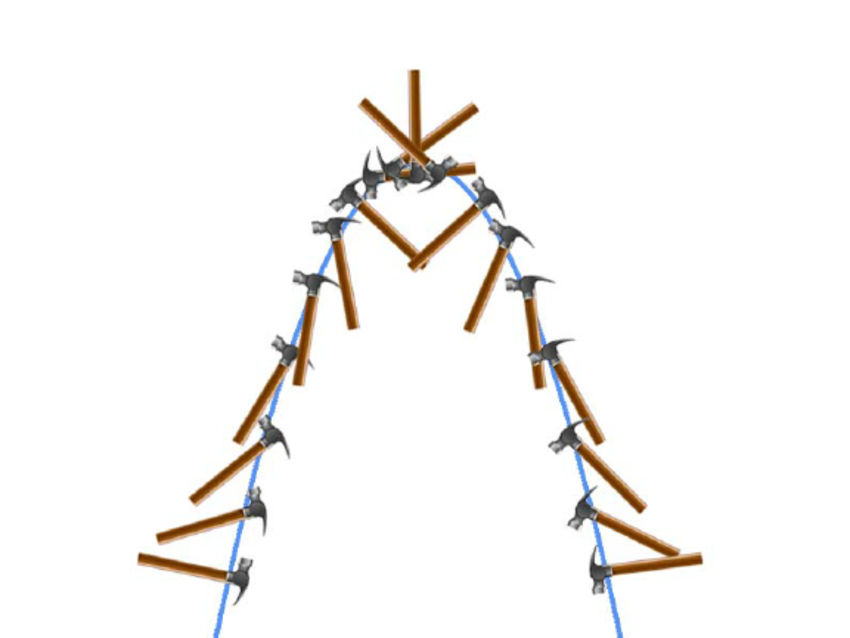
# P. Rule 105. EVERYTHING moves in the parabolar shape as it is thrown in the air. The motion of irregularly shaped objects, like a hammer, seems to be much more complicated. However, you must see through the propaganda and see that the hammer rotates around its center of mass, and the motion of the center of mass of the hammer still follows a parabola just like a ball or something else with a symmetrical shape/constant density. Evidence:
Regardless of any rotation an object may be experiencing (as depicted with the hammer), you can consider the force of gravity to be acting directly on the center of mass. This holds true for all objects in projectile motion.
# P. Rule 106. Expanding on the concept of Rule 105, systems of objects also have their own center of mass (discerned through the location and individual masses/densities of all of the objects) that follows the same old parabolar projectile motion path. This is in spite of the fact that the balls are all moving relative to one another.
# P. Rule 107. When the object is in a constant gravitational field, the center of mass is the same as the center of gravity. We generalize Earth to have a constant gravitational acceleration (9.81 m/s²), even though that number actually varies at different locations on Earth (see Rule 15).
# P. Rule 108. The center of mass of an object is not necessarily always located on the object itself - think of a donut, for example. Constant density + constant shape = center of mass in the geometric center, regardless of if there is anything in the center.
# P. Rule 109. When you apply a force somewhere to the sides of the center of mass of the system, the applied force will rotate the system. If you apply a force to an object at, or directly toward, its center of mass (which is the case in practically every problem you will have to deal with), the force applied will not cause the object to rotationally accelerate - the force will only cause a linear acceleration of the object.
Note that even though many problems state that a force is pushing at an angle, 99% of the time that force is still being directed on the center of mass, just from a new angle of attack.
# P. Rule 110. When hung or tipped, the force of gravity will pull directly upon the center of mass of the object to bring the center of mass back to its lowest point. When you tip one of those untippable cups, the center of mass is getting raised in the air (because it was already very low), and so the force of gravity will naturally pull downward on the center of mass, as a result causing the cup to stand upright again.
# P. Rule 111. There is a trick you can use to determine the center of mass of a flat object in reality: simply hang the object up by one end and place tape vertically, from where the object is hung to the bottom. Then, turn the object and repeat the process. Where the two lines of tape intersect is where the enter of mass will be.
# Point Object/Point Particle: An object small enough that its size and shape are irrelevant - it can just be considered to be a dot in space, possibly with a mysterious mass associated with it as well.
# Centroid: The unweighted, geometric center of a system. If there are two objects in a system, and one is 1000x the mass of the second, the centroid will still be directly in the middle between them. Thus, the centroid is the ignoramus's center of mass.
# P. Rule 112. Calculating the center of mass of a system is lightwork. First, collect the mass and positions in the cartesian plane of each individual object of the system. This system works best with point objects. A general equation for the center of a system is flexible to work with any number of points, but must be solved separately for the x, y, and z directions of the points, as follows:
xcom = (Σ mnxn) / (Σ mn)
ycom = (Σ mnyn) / (Σ mn)
zcom = (Σ mnzn) / (Σ mn)
This equation is described variously as the "system of particles" equation, or simply the "particle system" equation. Each of the known "positions" of the particles are with respect to a zero reference point (usually the origin, though it can differ depending on the problem, requiring the individual to perform extra calculations).
A revolutionary, modern super-equation fit for the 21st century has recently been discovered to combined ALL THREE directions in three-dimensional space into a single, efficient, all-use equation. It is as follows:
rcom = (Σ mnrn) / (Σ mn)
Since r contains all three of the directions (xî + yĵ + zk̂), it returns the exact center of mass three-dimensionally.
Going further, as a true testament to the progress of science, scientists have discovered that taking the derivative of this super-equation will result in a system-velocity equation, which describes the velocity of the center of mass of a system of particles:
vcom = (Σ mnvn) / (Σ mn)
# P. Rule 113. In order to find the change in position of the center of mass of a system, you must use the center of mass equation for the initial position, and then for the final position, and subtract former from the ladder, in the delta "change in" tradition.
# P. Rule 114. On method of finding the center of mass of irregular objects is to split the object into multiple, normally shaped objects (like square, rectangles, triangles, and other basic shapes) that can be used in a system of particles type problem, as described in Rule 112.
# P. Rule 115. If you are not given mass in a problem with multiple objects, do not fear: When all the pieces of the object (or all of the parts of a system) have the same density and thickness, the center of mass equation can be altered as follows:
xcom = (A1x1 + A2x2 + ...) / (A1 + A2 + ...)
This is derived through the following means:
ρ1 = ρ2
(m1 / ∀1) = (m2 / ∀2)
(m1 / (A1 × t)) = (m2 / (A2 × t))
(m1 / A1) = (m2 / A2)
m1 = (A1 / A2) × m2
From there, you can just plug in that value into the center of mass equation, causing every term to have the same mass. Thus, the mass can be canceled out, and now only the area of each object is needed to complete the problem.
# P. Rule 116. If the object has a hole in it, you can calculate the center of mass by imagining the hole and the object it is part of as being separate particles, calculating the center of mass for each individually. From there, you can use the classic 'system of particles' equation (see Rule 112). However - be careful to instead SUBTRACT the terms relating to the hole in the equation instead of adding them, in order to account for the center of mass being shifted away from the part of the object with the hole.
# Uniform: When applied in the context of all of this center of mass nonsense, it means that the object has constant density.
# P. Rule 117. It is possible, more efficient, and fairly easy to use calculus in order to calculate the center of mass, deriving the equation for it from the density equation and the system of particles equation.
First, the summation of all of the particles in the system must be made to account for an infinite amount of particles, the mass of which will each approach zero as they get more numerous and more representative of actual particles. This can be represented as follows:
Each infinitesimally small particle can be called "dm", and the whole expression can be written as the following integral:
$$x_{cm} = \frac{1}{m_{\text{total}}} \int x \, dm$$
This is the universal equation for density, but note that finding what equality will turn dm into dx in the first step every time the equation is used. Determining the mass through whatever means necessary is also very important.
Basic example: Assume a triangle with the thickness t and a uniform volumetric mass density p, with a base a and a height b. Since we cannot directly take the integral of x with respect to mass, we will first use the density equation to determine relationship between x-direction and mass. Since dm (each rectangle subdivision of the object) and the object itself have the same density,
ρ = (mtotal / Vtotal) = (dm / dV)
dm = ρdV
And now, since the volume of the dm box is equal to length × width × height, a new value for dV can also be determined.
dV = y × t × dx
Now,
dm = ρ × y × t × dx
From there, the original (mtotal / Vtotal) version of density can be recalled and fully expanded while being set equal to the fully fleshed out second side of the equation:
(mtotal / Vtotal) = (mtotal / ½abt) = (2mtotal / abt)
dm = ρ × y × t × dx
= (2mtotal / abt) × y × t × dx
=(2ymtotal / ab) × dx
FINALLY,
$$x_{cm} = \frac{1}{m_{\text{total}}} \int_0^a x \left( \frac{2ym_{\text{total}} }{ab} \right) \, dx$$
Moving out all of the constants, you get:
$$x_{cm} = \frac{2}{ab} \int_0^a xy \, dx$$ Still, the y must be replaced with something else in order to take the integral, and so the basic slope formula can be used for this purpose:
y = mx + y0
y = (b/a) × x
$$x_{cm} = \frac{2}{ab} \int_0^a x \left( \frac{b}{a} x \right) \, dx$$ =
$$x_{cm} = \frac{2}{a^2} \int_0^a x^2 \, dx$$
Solving this problem out, you get (2/3) × a.
# P. Rule 118. Despite what you have been indoctrinated into believing in school, there are actually THREE (3) types of density relating to mass.
- Volumetric Mass Density: ρ = (m / V). Defined by Wikipedia as "a substance's mass per unit of volume". Note that there are actually other types of volumetric density, such as volumetric weight density & volumetric charge density.
- Surface Mass Density: σ = m / A.
- Linear Mass Density: λ = m / L. The amount of mass per unit length.
# P. Rule 119. Internal forces will occur when particles within the system collide with one another. However, those internal forces form a Newton's 3rd Law force pair and cancel one another out. Thus,
ΣFinternal = 0
Thus, even when a collisions occurs with the system, if there is no net external force acting on the system, the acceleration will be zero and thus the velocity (and linear momentum) of the center of mass of the system will remain constant.
VIII.II Momentum Basics.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: p = m × v
p = Momentum.
m = Mass.
v = Velocity.
Definition: "Inertia in Motion", the property of an object in motion to remain in the state of motion. Is always in the same direction as the velocity.
Note that when you are calculating momentum, you calculate momentum in reference to individual objects of a system, not forces. This is why in conservation of momentum you only include the objects of the system in your calculations.
# NEW VERSION(S) OF THE 2ND LAW OF MOTION:
ΣF = (∆p / ∆t) (Average)
ΣF = (dp / dt) (Instantaneous)
This equation is derived from the original 2nd law and from the momentum equation. It is so obvious I will not bother to reproduce the proof here. If you need to derive it, think very hard for a few seconds.
The original version of the 2nd law of motion, with its m × a and whatnot, assumes that mass is constant. However, in our modern day and age, we cannot settle for this. These equations enable mass to change - rockets, for example, will lose mass as they expel fuel, and still the momentum version of the 2nd law will remain perfectly usable.
# Impulse: VECTOR.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: J = ∆p
J = Impulse.
p = Momentum.
Alt. Equation: $$\vec{J} = \int_{t_i}^{t_f} \sum \vec{F} \, dt$$ (Derived from the instantaneous definition of the new version of the 2nd law of motion).
J = Impulse.
F = Force.
ti = Time Initial.
tf = Time Final.
Alt. Alt. Equation: J = Favg × ∆t (used for approximations)
J = Impulse.
Favg = Average Force.
∆t = Change in Time.
Definition: Just another way of referring to the change in momentum, in a cooler way.
# P. Rule 120. Impulse Approximation:
During collisions with short time intervals, the force of impact is much larger than all the other forces, therefore all other forces can be considered to be negligible when compared to the impact force and the net force is approximately equal to the force of impact.
tl;dr: With collisions that have short ∆t, ΣF ≈ Fimpact
The shorter the time length, the more accurate this approximation gets.
# P. Rule 121. With respect to impulse, consider time and force to be inversely proportional to eachother. Because the impulse of a collision will be constant, if there is a shorter time length of the collision, the Force will be higher, and if the collision occurs over a longer period of time, then the force will be smaller, since either way they need to equal the same constant (impulse) when multiplied.
# P. Rule 122. Conservation of Momentum:
A system is "isolated" when the net force on the system is zero. Momentum is conserved in all isolated systems:
Σpi = Σpf
As you can see, this equation accounts for changes in the mass of a system, so long as there is a proportional change in the velocity that will result in momentum being conserved. The initial point is assumed to be right before the collision or explosion, and the final point is assumed to be right after.
Momentum is conserved during all collisions and explosions. In physics terms, an explosion is essentially just a collision in reverse.
REMEMBER: Conservation of momentum can be done in individual directions or combined - finding values using a conservation equation isolated to a particular direction can be very useful and necessary at times.
For example: when you stand on a skateboard and you are holding a ball, the system consists of you, the skateboard, and the ball. You start off with an initial momentum of zero, because you are not moving. When you throw that ball in one direction, the ball obtains a velocity, which means it patently does not have a momentum of zero. In order for the net momentum of the system to be zero (since one part of the system is moving), the other part of the system must move in the opposite direction (with the same force, of course) so that the total momentum of the system will cancel out and remain zero. This follows both the 3rd law of motion and ensures the conservation of momentum.
# P. Rule 123. TYPES OF COLLISIONS:
Momentum is conserved in all of these, because they are all collisions.
- Elastic Collision: A collision in which the total kinetic energy of a system of the two colliding bodies is unchanged by the collision, conserving the kinetic energy of the system. Generally, the objects "bounce" off of one another in these types of collisions.
- Inelastic Collision: A collision in which kinetic energy is NOT conserved. In these collisions, some energy is converted from kinetic energy to other forms of energy, like thermal, light, or sound energy (think friction). Inelastic collisions cause objects to deform, cauusing the kinetic energy to turn into thermal energy.
- Perfectly (or 'completely') Inelastic Collision: The objects stick to one another upon colliding. This is scenario with the greatest possible loss of kinetic energy. However, this does not necessarily mean that the objects will stop moving - if you throw a ball into a box on a skateboard, that will be a perfectly inelastic collision even though the skateboard and the entire system will begin moving (due to the conservation of momentum, assuming that the ball is apart of the system).
# THE LAST WORD:
The Equation of Conservation of Energy requires a minimum of two objects. Of course, this does not mean that these objects must remain constant throughout the problem - you could possibly have a single object in the beginning that could explode into three objects, resulting in one object on the left side of the equation and three on the right side. Or, possibly, you could have a Perfect Inelastic Collision occur, resulting in two objects on the left side and one object on the right.
The Force of Impact equation (the alt. 2nd law of motion equation) and the Impulse equations each only allow for one object.
It is easy to forget the point of Physics is to have FUN! Playing around with the variables is a great way to relieve stress.
