These are my complete notes for Rotational Dynamics in Classical Mechanics.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Rotational Dynamics (Classical Mechanics)
Table Of Contents
IX. Rotational Dynamics
IX.I Moment of Inertia.
Translational Motion = The movement through space of the center of mass of the object.
Rotational Motion = The movement of an object through circular motion about its center of mass.
A BICYCLE will be in both Translational and Rotational motion when it is in use.
# Moment of Inertia: SCALAR.
Units: Joules (Newton Meters).
Equation:
(for systems of particles) $$I = \sum_{n=1} m_n\,\, r_n^2$$ (for rigid objects with constant density) $$I = \int r^2 \, dm$$
I = Moment of Inertia.
m = The mass of each particle.
r = The distance each particle is from the axis of rotation (the center of the rotation).
dm = Each infinitesimally small particle composing the object.
Definition: Also known as Rotational Mass or Rotational Inertia. A measure of resistance to Angular Acceleration, as opposed to Inertial mass, which is a measure of an object's resistance to acceleration in general. For the full derivation of the formula (and how it connects into Rotational Kinetic Energy), see Rule 122.
The moment of inertia of an entire system is just the summation of all of the individual moments of inertias of the objects within the system. To sum rotational inertias, literally just add them all together, even if they are of different types: if a system contains a particle and a thin rod, then add the particle rotational inertia equation to the thin rod rotational inertia, which has an already known alternate equation (see "Basic Rotational Inertias"). Note: This is only so long as the inertias are calculated around the same axis of rotation.
If you ever need to find the rotational inertia of a non-particle that doesn't have a generalized inertia already known, then you need to use either the rotational kinetic energy equation (if you know the value (see Rule 122)), or the net torque equation (which is equal to I × α, see Rule 125).
In essence, the equations for moment of inertia state that as the distance from the axis of rotation increases, so will the moment of inertia. For example - if you have a broom and you try to rotate it from the brush, it will not be too difficult since most of the mass is located by the brush, but if you were to try to rotate the broom from the top of the handle, it will be much more difficult as the bulk of the mass has dramatically increased in its distance from the center of the rotation.
#
P. Rule .
Kinetic Energy of Rotation:
The Kinetic Energy of old has failed us. Since the classic kinetic energy formula is only with regard to the center of mass of the object (this is called "translational" kinetic energy), a uniform object in rotational motion would be considered to have zero kinetic energy - ignorantly. This equation is inadequate to deal with such pressing questions of modern Physics as the kinetic energy contained in a spinning object - all objects in motion must have kinetic energy.
Thus, a new form of kinetic energy must be discovered: the summation of the kinetic energies of every particle of the system, in the process reimagining the object as a system of particles, each with its own velocity that can contribute to the whole: $$\sum_{n=1} \frac{1}{2} m_n \left(v_n\right)^2$$ Since the velocity in this equation is the tangential velocity, the formula of tangential velocity can be substituted in, producing the following: $$\sum_{n=1} \frac{1}{2} m_n\,\, r_n^2\,\,\, ω^2$$ In all rigid objects with a constant shape, the angular velocity of each particle is the same, and so there is no need for the n subscript to be applied to the ω. Thus, when removing all constants from the equation, you are left with what is known as the Moment of Inertia, represented as the letter I: $$I = \sum_{n=1} m_n\,\, r_n^2$$ Now, the Rotational Kinetic Energy equation has been created: (1/2) × I × ω². The old Translational Kinetic Energy equation ((1/2) × m × v²) was only concerned with the motion of the center of mass of the object, and now, we can use the rotational KE to determine the energy of objects that are merely spinning.
During all conservation of mechanical energy problems, you must account for both Translational and Rotational Kinetic Energy. An object can be in rotational and translational motion at the same time, occurring when both the center of mass of the object is moving through space, and the object itself is in centripetal motion, such as when the object is rolling.
The Kinetic Energy of old has failed us. Since the classic kinetic energy formula is only with regard to the center of mass of the object (this is called "translational" kinetic energy), a uniform object in rotational motion would be considered to have zero kinetic energy - ignorantly. This equation is inadequate to deal with such pressing questions of modern Physics as the kinetic energy contained in a spinning object - all objects in motion must have kinetic energy.
Thus, a new form of kinetic energy must be discovered: the summation of the kinetic energies of every particle of the system, in the process reimagining the object as a system of particles, each with its own velocity that can contribute to the whole: $$\sum_{n=1} \frac{1}{2} m_n \left(v_n\right)^2$$ Since the velocity in this equation is the tangential velocity, the formula of tangential velocity can be substituted in, producing the following: $$\sum_{n=1} \frac{1}{2} m_n\,\, r_n^2\,\,\, ω^2$$ In all rigid objects with a constant shape, the angular velocity of each particle is the same, and so there is no need for the n subscript to be applied to the ω. Thus, when removing all constants from the equation, you are left with what is known as the Moment of Inertia, represented as the letter I: $$I = \sum_{n=1} m_n\,\, r_n^2$$ Now, the Rotational Kinetic Energy equation has been created: (1/2) × I × ω². The old Translational Kinetic Energy equation ((1/2) × m × v²) was only concerned with the motion of the center of mass of the object, and now, we can use the rotational KE to determine the energy of objects that are merely spinning.
During all conservation of mechanical energy problems, you must account for both Translational and Rotational Kinetic Energy. An object can be in rotational and translational motion at the same time, occurring when both the center of mass of the object is moving through space, and the object itself is in centripetal motion, such as when the object is rolling.
# Basic Rotational Inertias:
Here are the Moments of Inertia of some basic rigid objects with constant density. Recall that 'M' is mtotal.
Type, Axis of Rotation
Thin rod of length L, about its center of mass: I = (1/12) × M × L²
Thin rod of length L, about one end: I = (1/3) × M × L²
Thin hollow cylinder (hoop), about its long cylindrical axis: I = MR²
Solid cylinder/disk, about its long cylindrical axis: I = (1/2) × M × R²
Solid sphere, about its center of mass: I = (2/5) × M × R²
Thin hollow sphere/shell, about its center of mass: I = (2/3) × M × R²
Solid slab/block, about its center of mass (perp.): I = (1/12) × M × (a² + b²)
Note that in all where length is irrelevant to the moment of inertia, such as with the cylinders, an object of that type of any length will have the same moment of inertia, from a ring to a mile-long tube.
Derivations: [1] [2] [3]
IX.II Torque.
Units: Newton Meters (Joules). When in reference to Torque, the explicit units "Newton Meters" are used instead of "Joules" to differentiate it from the Scalar units of Work and Kinetic Energy.
Equation:
τ = r × F × sinθ
τ = Torque.
F = The magnitude of the force causing the torque.
r = The magnitude of the position vector from the axis of rotation to the point the force is applied to the object, the magnitude being the base distance. Thus, the farther the distance from the AOR that the force is applied, the greater the r.
θ = The angle between the direction of r and the direction of F.
Definition: The ability of a force to cause an angular acceleration in an object. Just as translational motion is caused by a net force (the ability to cause an acceleration in an object), rotational motion is caused by a net torque. Of course, torque is caused by a force.
The direction of torque, being a result of the cross product, requires only the traditional right-hand rule for determination, back in Subsection III.II. Note that torque is in the same direction as the angular acceleration that it produces, which is also the same direction as the angular velocity or angular displacement, determined through the Rotational RHR (see Rule 51). Choose which one you use based on the parameters of the problem/situation. Either rule patently does not give you the direction of force - figure that out using vector decomposition or something else.
#
P. Rule .
ANALYSIS OF TORQUE.
Think of the opening of a door: The door handle will be positioned as far from the hinges as possible, since the hinges represent the axis of rotation. If you push on the part of the door close to the hinges, it will barely budge. This is because by pushing farther away from the hinges, a larger r value is created (thus producing more torque), and by pushing close the hinges, a smaller r value is created, thus creating less torque.
Furthermore, the angle at which the door is pushed will matter significantly due to the sin curve - the maximum value for the sine of angle is at 90 degrees (1), so pushing perpendicular to the door will result in the most angular acceleration, while other degrees will produce less. A perpendicular force would produce the minimum force necessary to produce torque - other angles at which force can be applied would require higher magnitudes of force to reach the same level of torque. If you push directly parallelly to the direction of r, e.g. directly toward the hinges from the side of the handle, then an angle of 180 will be created, resulting in no torque whatsoever (since sin(180) = 0).
UNDERSTANDING OF THE UTMOST IMPORTANCE:
θ represents the angle between the DIRECTIONS of r and F. You must always be careful to determine the directions of r and F before you make any judgements as to θ.
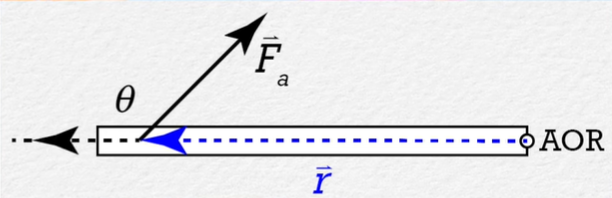
Understand that the direction of the r vector is whichever one in which the distance from the axis of rotation is increasing. Thus, for a door, the direction will be toward the knob and away from the hinges. An example of these concepts can be seen in the figure below, which depicts a door with an unusual force being applied and the resultant θ:
A diagram of a door (the hinges/axis of rotation labeled as AOR) having a non-perpendicular force applied to it. This produces a θ to the left of the force. This highlights a difference between torque and work. Courtesy of Flipping Physics.
Torque is NOT the same as work - torque uses the direction of the variables.
Think of the opening of a door: The door handle will be positioned as far from the hinges as possible, since the hinges represent the axis of rotation. If you push on the part of the door close to the hinges, it will barely budge. This is because by pushing farther away from the hinges, a larger r value is created (thus producing more torque), and by pushing close the hinges, a smaller r value is created, thus creating less torque.
Furthermore, the angle at which the door is pushed will matter significantly due to the sin curve - the maximum value for the sine of angle is at 90 degrees (1), so pushing perpendicular to the door will result in the most angular acceleration, while other degrees will produce less. A perpendicular force would produce the minimum force necessary to produce torque - other angles at which force can be applied would require higher magnitudes of force to reach the same level of torque. If you push directly parallelly to the direction of r, e.g. directly toward the hinges from the side of the handle, then an angle of 180 will be created, resulting in no torque whatsoever (since sin(180) = 0).
UNDERSTANDING OF THE UTMOST IMPORTANCE:
θ represents the angle between the DIRECTIONS of r and F. You must always be careful to determine the directions of r and F before you make any judgements as to θ.
Understand that the direction of the r vector is whichever one in which the distance from the axis of rotation is increasing. Thus, for a door, the direction will be toward the knob and away from the hinges. An example of these concepts can be seen in the figure below, which depicts a door with an unusual force being applied and the resultant θ:
A diagram of a door (the hinges/axis of rotation labeled as AOR) having a non-perpendicular force applied to it. This produces a θ to the left of the force. This highlights a difference between torque and work. Courtesy of Flipping Physics.
Torque is NOT the same as work - torque uses the direction of the variables.
# Moment Arm/Lever Arm: The Perpendicular distance between the line of action of the force and the axis of rotation. The "line of action" is just the artificial extension of the force through space until it can form a right angle with the also artificially created "moment arm". Imagine that r and F are two sides of a right triangle. The third side, which will never be the hypotenuse, is a component of the r position vector. The third side will thus be perpendicular to the force, and, as the perpendicular component of r, is known as the "moment arm" or the "lever arm".
When θ is 90 degrees (a perpendicular force), then r and the moment arm are equal in magnitude, and the Force is the hypotenuse.
Through the forces of trigonometry, the moment arm is equal to r × sinθ, since the sine of any supplementary angles (θ1 and θ2 in the figure) will produce the same value, as one can demonstrate using the sine curve.
This is something that you are guaranteed to do during a problem at some point: use the moment arm to simplify an equation involving a moving particle into just constants. The angular momentum for a moving particle equation, r × m × v × sinθ (see Rule 136), can be simplified very quickly into y × m × v, y being the moment arm perpendicular to the distance between the particle and the center of mass, and to the force. This can be done through pure trigonometry, since y = r × sinθ.
An example of how the moment arm can be constructed using the line of action of the force, and the position vector. Courtesy of Flipping Physics.
#
P. Rule .
Torque Summations:
To sum the torques of the various forces acting upon a position vector, you merely have to add all of the calculated torques of each force together (calculated using the torque equation seen in the torque definition). Make sure to determine the direction of each torque using the right-hand rule, as this will tell you which torques are negative or positive. The sign of your answer will serve as the "direction" of the torque, either positively or negatively perpendicular to the force and position vector.
When summing the torques, you have to sum the torque of EVERY force, including gravity and the normal force. If the axis of rotation is centered at the center of mass, then the torque of gravity can be set to zero since it has an r of 0. You must be careful not to place the normal force as being located at the center of mass of the object - that is an old oversight that must be corrected - See Rule 139.
Note that the summed torques is one half of an equality described in the rotational form of Newton's Second Law (Rule 125), which is the rotational equivalent to ΣF = ma. If a question is only asking to find "the net torque", just sum the torques without setting it equal to I × α.
To sum the torques of the various forces acting upon a position vector, you merely have to add all of the calculated torques of each force together (calculated using the torque equation seen in the torque definition). Make sure to determine the direction of each torque using the right-hand rule, as this will tell you which torques are negative or positive. The sign of your answer will serve as the "direction" of the torque, either positively or negatively perpendicular to the force and position vector.
When summing the torques, you have to sum the torque of EVERY force, including gravity and the normal force. If the axis of rotation is centered at the center of mass, then the torque of gravity can be set to zero since it has an r of 0. You must be careful not to place the normal force as being located at the center of mass of the object - that is an old oversight that must be corrected - See Rule 139.
Note that the summed torques is one half of an equality described in the rotational form of Newton's Second Law (Rule 125), which is the rotational equivalent to ΣF = ma. If a question is only asking to find "the net torque", just sum the torques without setting it equal to I × α.
#
P. Rule .
Rotational Form of Newton's Second Law:
Στ = I × α.
The sum of the torque (that of the various forces acting upon an object) is equal to the moment of inertia times the angular acceleration. The angular acceleration is directly proportional to the magnitude of the net torque, and is inversely proportional to the moment of inertia.
In order to use this equation, you must identify the objects with torque, the axis of rotation of them, and which direction is positive torque.
Στ = I × α.
The sum of the torque (that of the various forces acting upon an object) is equal to the moment of inertia times the angular acceleration. The angular acceleration is directly proportional to the magnitude of the net torque, and is inversely proportional to the moment of inertia.
In order to use this equation, you must identify the objects with torque, the axis of rotation of them, and which direction is positive torque.
# Rotational Equilibrium: When, as a result of a net zero torque (which in turn causes zero angular acceleration), the object remains at rest or at a constant angular velocity.
This is just like Translational Equilibrium, which is when a net force of zero on an object (and thus zero acceleration) results in the object being either at rest or at a constant velocity.
Note that it is impossible for the rotational inertia to be equal to zero so long as there is any mass located away from the axis of rotation, which is in all real circumstances.
# Static Equilibrium: A state in which an object is at rest and not rotating. Thus, the object is in both Translational and Rotational Equilibrium at the same time. Additionally, the net torque of any axis of rotation will equal zero.
The ability to use both torque and regular force equations can be super useful, especially with the ability to place the axis of rotation on any spot (and thus nullifying any forces acting on that spot in the torque equations, since the r for that force would be zero).
#
P. Rule .
In all situations, if there are objects that are on top of other objects, and you are including the bottom objects in your force summation, then you do not need to include the force normals of the objects on top, only their forces of gravity. This is because the weight of the top objects will just contribute to the force normal of the bottom object.
Secondly, ALWAYS include ALL of the objects in the summation of the torques, including the objects on bottom and on top and anything in between. When determining if the torques are positive or not, don't forget you need to use the old right hand rule to figure it out, using the forces as your guide. Draw out the free-body diagram and draw the arrows on the forces to make it easier on yourself.
Don't forget the principle of single direction (see Rule 76) in all pulley problems. The direction you decide the torque to be moving in will change how you conduct force summations for any hanging objects, summing with regard to the direction that you decided would be positive, whether it be the clockwise or counter-clockwise movement of the pulley. Thus, for an object on the side of the pulley that would denote positive movement (whatever you decided that means) would have the force of gravity as a negative force, while a hanging object on the other side would have gravity as a positive.
Secondly, ALWAYS include ALL of the objects in the summation of the torques, including the objects on bottom and on top and anything in between. When determining if the torques are positive or not, don't forget you need to use the old right hand rule to figure it out, using the forces as your guide. Draw out the free-body diagram and draw the arrows on the forces to make it easier on yourself.
Don't forget the principle of single direction (see Rule 76) in all pulley problems. The direction you decide the torque to be moving in will change how you conduct force summations for any hanging objects, summing with regard to the direction that you decided would be positive, whether it be the clockwise or counter-clockwise movement of the pulley. Thus, for an object on the side of the pulley that would denote positive movement (whatever you decided that means) would have the force of gravity as a negative force, while a hanging object on the other side would have gravity as a positive.
#
P. Rule .
To solve static equilibrium problems, you can chose 1 of two placements of the axis of rotation for your torque summations:
1. You can set the axis of rotation all the way to the end of the main object (the saw or meterstick or whichever similar object), which can best be done in circumstances where the force normal has already been determined (whether through the y-direction force summation or other means).
2. You can set the axis of rotation to be at an exact point, whether one you want to find (such as a point whose r value you are trying to find) or one you want to remove all together in order to isolate another variable (in situations which you have two unknown variables, and placing the axis of rotation upon one point will remove that variable, allowing the other one to be solved).
1. You can set the axis of rotation all the way to the end of the main object (the saw or meterstick or whichever similar object), which can best be done in circumstances where the force normal has already been determined (whether through the y-direction force summation or other means).
2. You can set the axis of rotation to be at an exact point, whether one you want to find (such as a point whose r value you are trying to find) or one you want to remove all together in order to isolate another variable (in situations which you have two unknown variables, and placing the axis of rotation upon one point will remove that variable, allowing the other one to be solved).
#
P. Rule .
There is a trend in Physics and Mathematics equations that you will see rather commonly: Lowercase letters are in reference to variables, like the 'r' and 'dm' of the integral equation of moment of inertia equations. Uppercase letters, on the other hand, are in reference to constants, such as the 'R', 'M', and 'L''s of the basic rotational inertias.
#
P. Rule .
Parallel Axis Theorem:
Iparallel = ICOM + M × D²
Iparallel = The moment of inertia parallel to an axis through center of mass.
ICOM = The moment of inertia going directly through an axis through center of mass.
M = The total mass of the rigid body.
D = The distance from the center of mass to the new axis. This is NOT the distance from the old axis of rotation to the new one, it is the distance from the center of mass.
This theorem is an easy way to determine the moment of inertia of a rigid body, rotating about an axis parallel to the true axis that runs through the center of mass of the rigid body. This theorem greatly simplifies the process of determining moment of inertia for various objects (given you already know the parent one), such as in determining the moment of inertia of a thin rod of length L about one of its ends, given you already know the moment of inertia of the rod rotating around its center of mass (e.g., you can determine the second value of "Basic Rotational Inertias" from the first).
Iparallel = ICOM + M × D²
Iparallel = The moment of inertia parallel to an axis through center of mass.
ICOM = The moment of inertia going directly through an axis through center of mass.
M = The total mass of the rigid body.
D = The distance from the center of mass to the new axis. This is NOT the distance from the old axis of rotation to the new one, it is the distance from the center of mass.
This theorem is an easy way to determine the moment of inertia of a rigid body, rotating about an axis parallel to the true axis that runs through the center of mass of the rigid body. This theorem greatly simplifies the process of determining moment of inertia for various objects (given you already know the parent one), such as in determining the moment of inertia of a thin rod of length L about one of its ends, given you already know the moment of inertia of the rod rotating around its center of mass (e.g., you can determine the second value of "Basic Rotational Inertias" from the first).
#
P. Rule .
Do not forget how to correlate rotational and linear acceleration/velocity - you learned this before.
On a pulley system in which a string pull downward upon the circular pulley, pulling into centripetal motion, the pulley will be accelerating (angularly) at a proportional rate to the string (linearly), since the string can only move downward as the pulley/circular object moves with it. In these circumstances, remember that the string is moving at a tangential acceleration, which already has a proportionality defined for it:
at = r × α.
Tangential Velocity is practically the same thing as well, just with angular velocity instead of acceleration.
Do not forget the basic equations of centripetal motion when doing problems involving torque and moment of inertia! Reflect and review the old equations here.
On a pulley system in which a string pull downward upon the circular pulley, pulling into centripetal motion, the pulley will be accelerating (angularly) at a proportional rate to the string (linearly), since the string can only move downward as the pulley/circular object moves with it. In these circumstances, remember that the string is moving at a tangential acceleration, which already has a proportionality defined for it:
at = r × α.
Tangential Velocity is practically the same thing as well, just with angular velocity instead of acceleration.
Do not forget the basic equations of centripetal motion when doing problems involving torque and moment of inertia! Reflect and review the old equations here.
#
P. Rule .
Negligible friction: Though a pulley can be stated to have "negligible friction", if this were actually true, any strings/wire upon it would just slide off and the pulley would never rotate. The meaning of "negligible friction" when stated with regard to a pulley is that the Axle of the pulley, the center rotatinal axis, has negligible friction - the surface of the pulley still has the necessary friction to interact with the string, enough so that the acceleration of the pulley and the string are proportional to one another. See Rule 130 for an explanation.
# Cycloid: A curve traced by a point on a circle rolling in a straight line.
Cycloid. Courtesy of Wikimedia.
#
P. Rule .
All objects that roll without slipping, such as cylinders and all good tires, have a total kinetic energy that equals the sum of the translational and rotational kinetic energies of the object:
KEtotal = KET + KER
KEtotal = (½ × m × v²) + (½ × I × ω²)
The acceleration of all objects that roll without slipping only relies on three determinants: the force of gravity, the incline angle, and the coefficient of the moment of inertia. The lower the fraction for the rotational inertia equation (where both gravity and the incline are constant), the lower the percentage of the initial gravitational potential energy that will be converted into rotational kinetic energy as the object rolls without sliding. Thus, more of the potential energy will be converted directly into translational kinetic energy, and thus the object will have a higher final velocity, thus moving down the incline faster.
For example, if a hollow sphere and a solid sphere (the radius of each being negligible) were both to begin rolling down an incline at the same time, the solid sphere would reach the bottom first since it has a smaller moment of inertia than the hollow sphere: 2/5 < 2/3.
If you do not know either component variable of rotational inertia (either mass & length or mass & radius), then it can be better not to substitute in the equation for rotational inertia into the problem, to leave I as only one unknown in the rotational kinetic energy equation. Sometimes, problems will tell you the specificities for a known moment of inertia ("a thin rod that rotates around one end"), but they will only serve as red herrings when no information as to the components of inertial mass is given, and so isolating the variable I itself and solving it outright will be the correct solution.
Do not fall into the dogma of having to substitute every possible equation in at all times - solving something on a higher level first can help you in many different ways.
KEtotal = KET + KER
KEtotal = (½ × m × v²) + (½ × I × ω²)
The acceleration of all objects that roll without slipping only relies on three determinants: the force of gravity, the incline angle, and the coefficient of the moment of inertia. The lower the fraction for the rotational inertia equation (where both gravity and the incline are constant), the lower the percentage of the initial gravitational potential energy that will be converted into rotational kinetic energy as the object rolls without sliding. Thus, more of the potential energy will be converted directly into translational kinetic energy, and thus the object will have a higher final velocity, thus moving down the incline faster.
For example, if a hollow sphere and a solid sphere (the radius of each being negligible) were both to begin rolling down an incline at the same time, the solid sphere would reach the bottom first since it has a smaller moment of inertia than the hollow sphere: 2/5 < 2/3.
If you do not know either component variable of rotational inertia (either mass & length or mass & radius), then it can be better not to substitute in the equation for rotational inertia into the problem, to leave I as only one unknown in the rotational kinetic energy equation. Sometimes, problems will tell you the specificities for a known moment of inertia ("a thin rod that rotates around one end"), but they will only serve as red herrings when no information as to the components of inertial mass is given, and so isolating the variable I itself and solving it outright will be the correct solution.
Do not fall into the dogma of having to substitute every possible equation in at all times - solving something on a higher level first can help you in many different ways.
#
P. Rule .
The acceleration and velocities of the center of masses of objects that roll without slipping (translational, obviously) also have their own equations, totally identical to their tangential equivalents:
vcom = R × ω
acom = R × α
Thus, very importantly, in these circumstances, the angular and linear accelerations/velocities will be in the same direction. If you are not getting that when you solve the problem, change the positive direction of the torque.
The equation for the distance travelled by the center of mass of the rolling object is similar to the arc length equation:
∆xcom = R × ∆θ
vcom = R × ω
acom = R × α
Thus, very importantly, in these circumstances, the angular and linear accelerations/velocities will be in the same direction. If you are not getting that when you solve the problem, change the positive direction of the torque.
The equation for the distance travelled by the center of mass of the rolling object is similar to the arc length equation:
∆xcom = R × ∆θ
IX.III Angular Momentum.
#
P. Rule .
Angular Momentum: VECTOR.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: (For Rigid Objects with Shape)
L = I × ω
L = Angular Momentum, represented with an 'L' instead of rho.
I = Moment of Inertia.
ω = Angular Velocity.
Definition: "Rotational Inertia in Motion", the property of an object in centripetal motion to remain in the state of centripetal motion.
Notice that since angular momentum and angular velocity are directly proportional vectors, they must be in the same direction. Determine direction using the rotational right hand rule. Furthermore, L has an inherent axis of rotation that must be identified every time, like torque and rotational inertia. Watch this for the derivation of the equation.
Units: (kg) × (m / s), occasionally known as Newton Seconds.
Equation: (For Rigid Objects with Shape)
L = I × ω
L = Angular Momentum, represented with an 'L' instead of rho.
I = Moment of Inertia.
ω = Angular Velocity.
Definition: "Rotational Inertia in Motion", the property of an object in centripetal motion to remain in the state of centripetal motion.
Notice that since angular momentum and angular velocity are directly proportional vectors, they must be in the same direction. Determine direction using the rotational right hand rule. Furthermore, L has an inherent axis of rotation that must be identified every time, like torque and rotational inertia. Watch this for the derivation of the equation.
#
P. Rule .
Conservation of Angular Momentum:
ΣLi = ΣLf
Expanded, this is the following:
Ii × ωi = If × ωf
Add as many additional angular momentums into the equation as there are objects in the system.
The conservation of angular momentum equation can be easily derived from a special case of the net external torque equation:
Στexternal = (∆Lsystem / ∆t)
Thus, if the object is not in centripetal motion at the beginning of the event (initial torque = 0), then if angular momentum is conserved, it will continue to have 0 centripetal motion at the end. If an external force causes centripetal motion to be created, then angular momentum is not conserved. See Rule 100 & Rule 101 to determine what forces are external or not.
General Example: When a figure skater pulls their arms inward during a performance, they will speed up. This is because they are reducing the distance of some amount of mass from their center of mass, thus decreasing the moment of inertia and causing the angular velocity to increase so that angular momentum is conserved.
ΣLi = ΣLf
Expanded, this is the following:
Ii × ωi = If × ωf
Add as many additional angular momentums into the equation as there are objects in the system.
The conservation of angular momentum equation can be easily derived from a special case of the net external torque equation:
Στexternal = (∆Lsystem / ∆t)
Thus, if the object is not in centripetal motion at the beginning of the event (initial torque = 0), then if angular momentum is conserved, it will continue to have 0 centripetal motion at the end. If an external force causes centripetal motion to be created, then angular momentum is not conserved. See Rule 100 & Rule 101 to determine what forces are external or not.
General Example: When a figure skater pulls their arms inward during a performance, they will speed up. This is because they are reducing the distance of some amount of mass from their center of mass, thus decreasing the moment of inertia and causing the angular velocity to increase so that angular momentum is conserved.
#
P. Rule .
In the SPECIFIC CASE of a point particle moving in a circle (centripetal motion), the following attributes are applicable to the particle:
1. Translational and Rotational Kinetic Energy will return the same value (only in these circumstances!). Choose either depending on what variables you have.
2. The angular momentum of the particle can be calculated using both the 'rigid object with shape' momentum equation (I × ω) and the translational point-particle momentum equation: Lparticle = r × m × v × sinθ.
r - The vector from axis of rotation to center of mass of particle.
m - The mass of the point particle.
v - The linear velocity of the point particle.
θ - The angle between the DIRECTIONS r and v, like torque.
This equation can additionally be used for all translationally moving point particles (which, indeed, have angular momentum insofar as how it could translate to another object obtaining that angular momentum following a collision).
Attribute #1 is also applicable for ellipses, though not #2.
1. Translational and Rotational Kinetic Energy will return the same value (only in these circumstances!). Choose either depending on what variables you have.
2. The angular momentum of the particle can be calculated using both the 'rigid object with shape' momentum equation (I × ω) and the translational point-particle momentum equation: Lparticle = r × m × v × sinθ.
r - The vector from axis of rotation to center of mass of particle.
m - The mass of the point particle.
v - The linear velocity of the point particle.
θ - The angle between the DIRECTIONS r and v, like torque.
This equation can additionally be used for all translationally moving point particles (which, indeed, have angular momentum insofar as how it could translate to another object obtaining that angular momentum following a collision).
Attribute #1 is also applicable for ellipses, though not #2.
#
P. Rule .
When a questions asks just for the "acceleration", "velocity", or "speed" of an object or a system, it is general principle to find the linear quanity, unless the question specifically asks for the angular version.
#
P. Rule .
Pulleys with Mass:
Pulleys with mass have rotational inertia. Pulleys without mass do not have rotational inertia.
Where as before, the force of tension (magnitude) applied on each side of the pully was the same, this is not the case in pulleys with mass: These pulleys will have rotational inertia due to their mass, and thus will resist angular acceleration, making the two forces of tension acting on either side of the pulley not necesarilly having the same magnitude.
In all problems where the pulley has mass, just incorporate it as another one of the objects you are findings the torques/angular momentum of, and summing the force normal & gravity of the pulley.
Pulleys with mass have rotational inertia. Pulleys without mass do not have rotational inertia.
Where as before, the force of tension (magnitude) applied on each side of the pully was the same, this is not the case in pulleys with mass: These pulleys will have rotational inertia due to their mass, and thus will resist angular acceleration, making the two forces of tension acting on either side of the pulley not necesarilly having the same magnitude.
In all problems where the pulley has mass, just incorporate it as another one of the objects you are findings the torques/angular momentum of, and summing the force normal & gravity of the pulley.
#
P. Rule .
In torque problems, you must always draw the normal force as originating at the point of contact, from the surface the object is resting on.
In the past, the normal force has been drawn as having the center of mass of the object as its origin - this is a simplification, a falsehood that is done purely in problems where such an oversight does not matter.
In problems involving Torque however, the location of the origin of the forces matters significantly, due to how torque is calculated. If the axis of rotation of an object is placed along the center of mass, then all torques acting at the center of mass are equal to 0 since they have a radius of 0 (see Rule 124). By placing the normal force on the center of mass of the object, you would be incorrectly excluding it from all torque summations in all situations where the axis of rotation is upon the center of mass.
In the past, the normal force has been drawn as having the center of mass of the object as its origin - this is a simplification, a falsehood that is done purely in problems where such an oversight does not matter.
In problems involving Torque however, the location of the origin of the forces matters significantly, due to how torque is calculated. If the axis of rotation of an object is placed along the center of mass, then all torques acting at the center of mass are equal to 0 since they have a radius of 0 (see Rule 124). By placing the normal force on the center of mass of the object, you would be incorrectly excluding it from all torque summations in all situations where the axis of rotation is upon the center of mass.